洛谷P1048 典型01背包问题

写在前面的话

蒟蒻在学习诸多图论算法之前，实际上没学过dp！

强说是学过也是只学了01背包，今天就来温习一下……

DP是啥？

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。

这是官方的解释，不过蒟蒻更喜欢把它的原理称作：

把计算结果记住。

实际上，我们可能已经早就见过动态规划了！它有很多别的名字，比如：

记忆化搜索
剪枝
用空间换时间
带备忘录（memo）的递归

发现了什么？我们很早就接触过动态规划！

这么一说，动态规划不是很难了吧！

动态规划的核心在状态转移方程，它的作用……本蒟蒻是这样理解的：

促进局部最优解向全局最优解发展

01背包DP

我们来仔细讲一下背包dp

题目传送门

代码：

#include<bits/stdc++.h>

using namespace std;

int t,m;//m<=100 物品个数;t<=1000 包包容量;

int times[101],values[101];

int dp[101][1001];//dp[i][j] means 以j为容量的包包，在前i个物品中进行放入的最大价值

int main(){

	scanf("%d %d",&t,&m);

	for(int i=1;i<=m;i++){

		scanf("%d %d",&times[i],&values[i]);

	}

	for(int i=1;i<=m;i++){

		for(int j=1;j<=t;j++){

			if(j>=times[i]){

				dp[i][j]=max(dp[i-1][j],dp[i-1][j-times[i]]+values[i]);

			}else{

				dp[i][j]=dp[i-1][j];

			}

		}

	}

	cout<<dp[m][t];

	return 0;

}

在阅读以下内容前请至少认真阅读一遍代码！

我们在这里将题中所给的各种采药时间视为占包包的空间就好了哈~

首先来看一下dp数组什么意思：

int dp[101][1001];//dp[i][j] means 以j为容量的包包，在前i个物品中进行放入的最大价值

假设我们有以下几个物品：

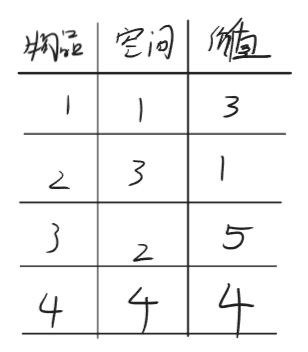
我们建立起对应的dp数组：

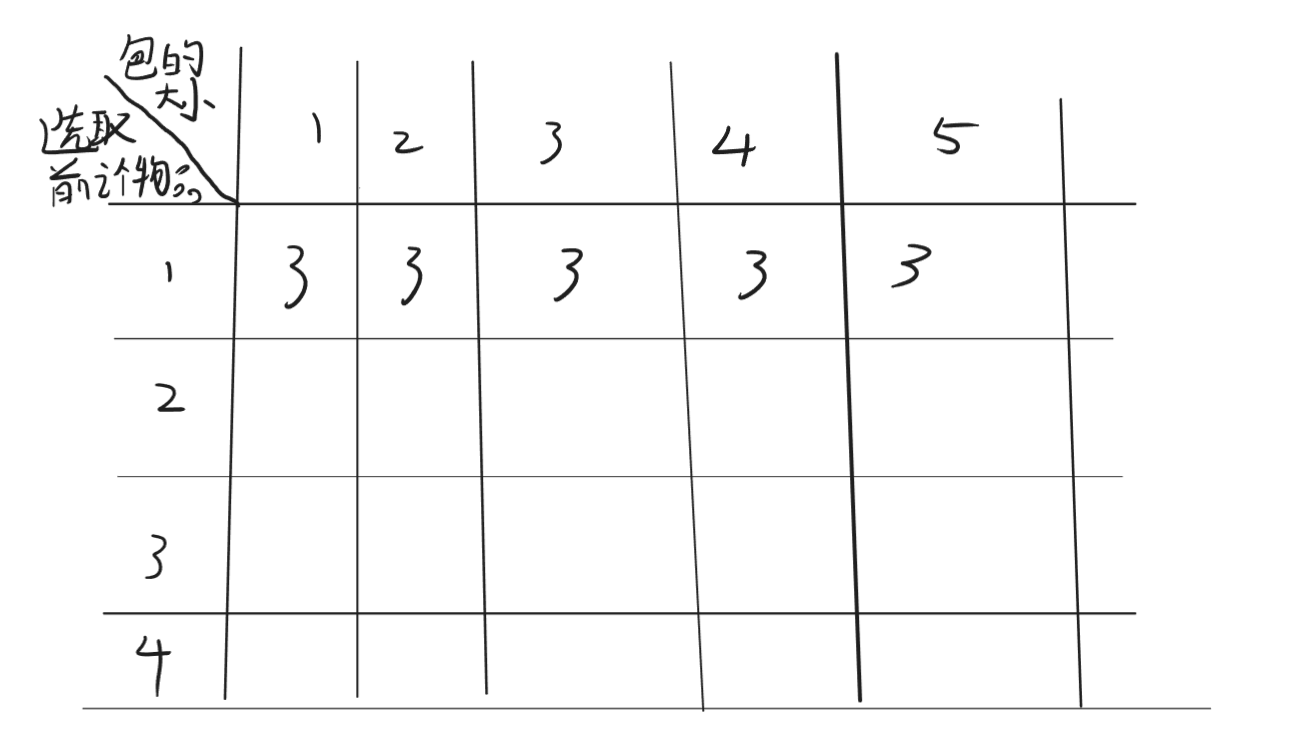
首先对表格第一行进行分析，我们可以看到，当只有物品1时，考虑的无非是放与不放的问题，我们发现物品1占用1个空间，若背包大小从1-5均可放入背包。

表格更新：

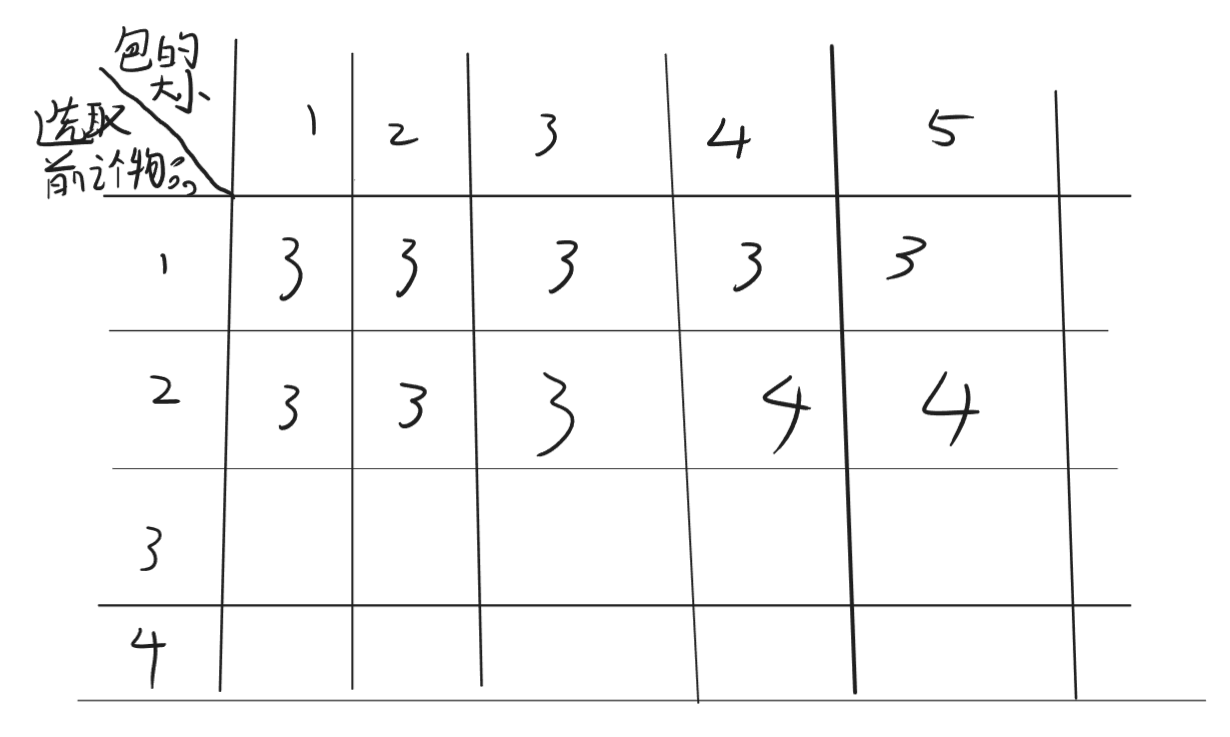
我们对第二行进行分析，此时我们有1和2两个物品可供选择，但是！我们发现2占空间为3！所以当背包空间在3以下时，2肯定放不进去，此时，我们只能将上方那个格子里的值给他平移下来。因为此时你既然无法放下新的这个，旧的也不能丢。别管上面那个是0还是不是0，平移下来一定是当前状态下最优解。

那么在3及以后，我们就要开始考虑是否要放入了。

发现，当包包空间为3时，我们只能要么只放一个1，要么只放一个2，换句话说，我们此时要比较上方那个格子的状态和加入这个物品前的最优解的值加上本物品的值的大小关系来进行决策。

加入这个物品前的最优解的值加上本物品的值这个怎么得到？

容易发现，根据最优解的原则，一个背包加上这个物品正好满了，这叫加入这个物品前的最优解。

于是乎，我们得到了一个状态转移方程！

dp[i][j]=max(dp[i-1][j],dp[i-1][j-times[i]]+values[i]);//times指的是占的空间，values指的是本物品价值

这行代码就是我们的状态转移方程。

根据以上我们总结出01背包核心思路：

如果当前背包容量$<$需决策物品的占的空间
- 直接平移同一列的上一个决策。
否则
- 执行状态转移方程，进行决策。

表格更新：

表格更新：

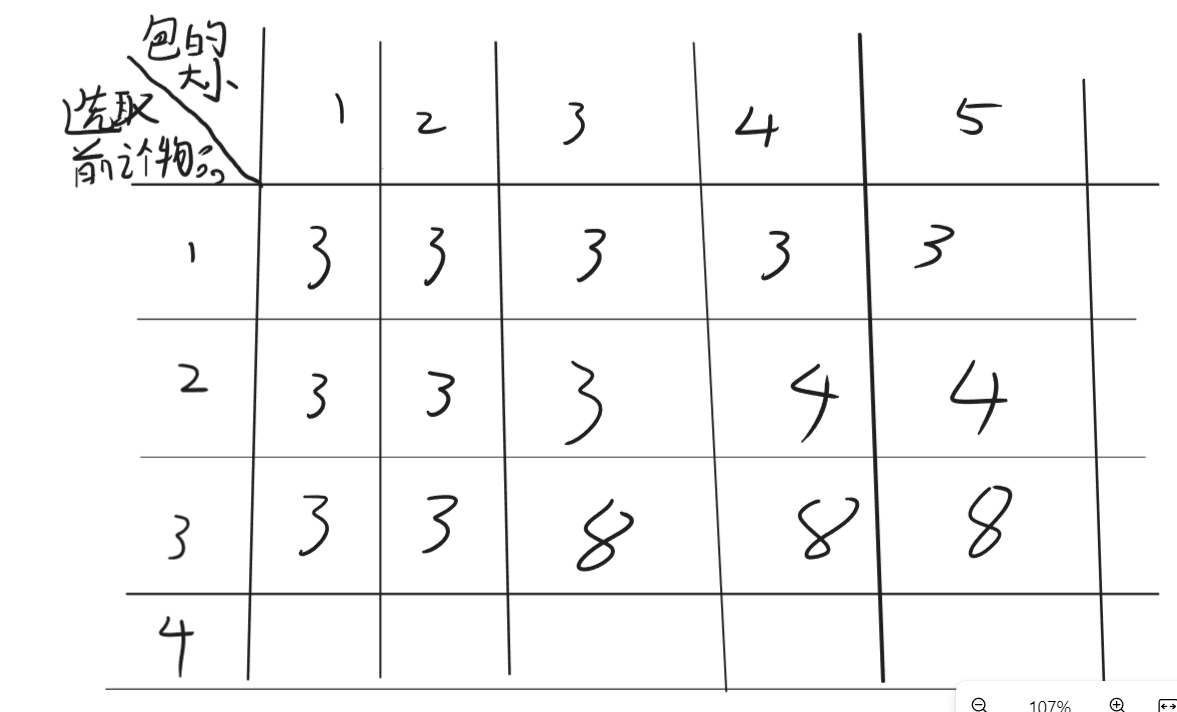
表格更新：

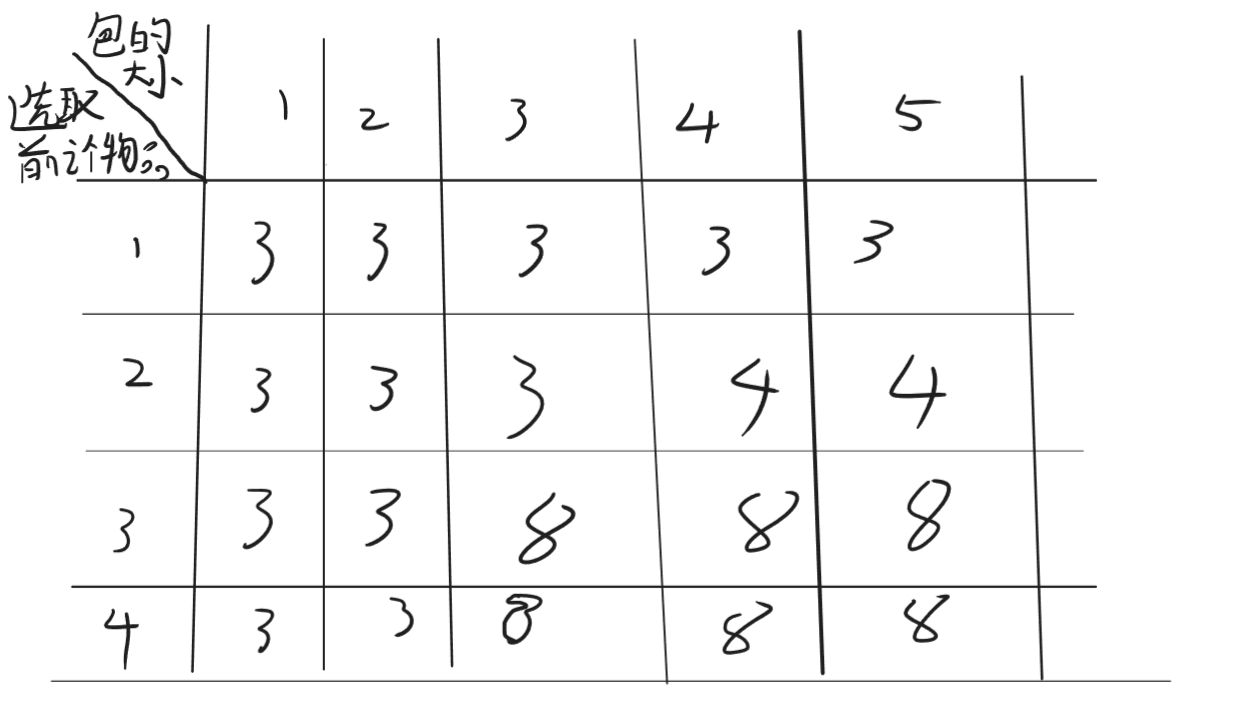
可以发现，最终dp[m][t]就是全局最优解。

写在最后

由于蒟蒻实在太弱，所以肯定讲的不是很好，有疏漏的地方。

蒟蒻过几天还想写一个有关最长上升子序列的题解……

完结撒花