BZOJ 1005 [HNOI2008] 明明的烦恼（组合数学 Purfer Sequence）

题目大意

自从明明学了树的结构，就对奇怪的树产生了兴趣......

给出标号为 1 到 N 的点，以及某些点最终的度数，允许在任意两点间连线，可产生多少棵度数满足要求的树？

Input

　　第一行为 N(0<N<=1000)，接下来 N 行，第 i+1 行给出第 i 个节点的度数 Di，如果对度数不要求，则输入 -1

Output

　　一个整数，表示不同的满足要求的树的个数，无解输出 0

做法分析

这题需要了解一种数列： Purfer Sequence

我们知道，一棵树可以用括号序列来表示，但是，一棵顶点标号（1~n）的树，还可以用一个叫做 Purfer Sequence 的数列表示

一个含有 n 个节点的 Purfer Sequence 有 n-2 个数，Purfer Sequence 中的每个数是 1~n 中的一个数

一个定理：一个 Purfer Sequence 和一棵树一一对应

先看看怎么由一个树得到 Purfer Sequence

由一棵树得到它的 Purfer Sequence 总共需要 n-2 步，每一步都在当前的树中寻找具有最小标号的叶子节点（度为 1），将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素，并将此叶子节点从树中删除，直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树

看看下面的例子：

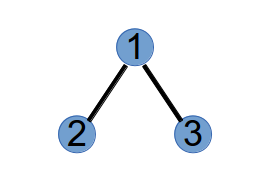
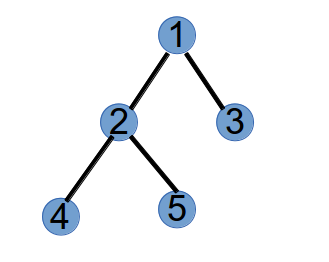
假设有一颗树有 5 个节点，四条边依次为：(1, 2), (1, 3), (2, 4), (2, 5)，如下图所示：

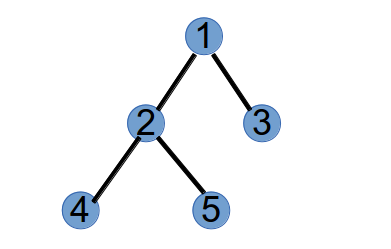
第 1 步，选取具有最小标号的叶子节点 3，将与它相连的点 1 作为第 1 个 Purfer Number，并从树中删掉节点 3：

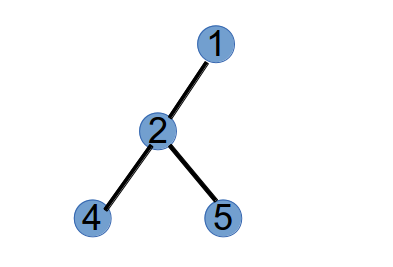
第 2 步，选取最小标号的叶子节点 1，将与其相连的点 2 作为第 2 个 Purfer Number，并从树中删掉点 1：

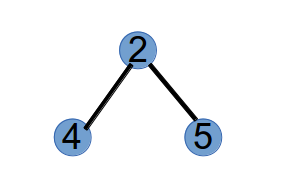
第 3 步，选取最小标号的叶子节点 4，将与其相连的点 2 作为第 3 个 Purfer Number，并从树中删掉点 4：

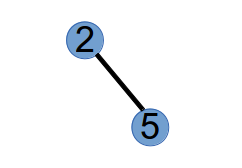
最后，我们得到的 Purfer Sequence 为：1 2 2

不难看出，上面的步骤得到的 Purfer Sequence 具有唯一性，也就是说，一个树，只能得到一个唯一的 Purfer Sequence

接下来看，怎么由一个 Purfer Sequence 得到一个树

由 Purfer Sequence 得到一棵树，先将所有编号为 1 到 n 的点的度赋初值为 1，然后加上它在 Purfer Sequence 中出现的次数，得到每个点的度

先执行 n-2 步，每一步，选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连，得到树中的一条边，并将 u 和 v 的度减一

最后再把剩下的两个度为 1 的点连边，加入到树中

我们可以根据上面的例子得到的 Purfer Sequence ：1 2 2 重新得到一棵树

Purfer Sequence 中共有 3 个数，可以知道，它表示的树中共有 5 个点，按照上面的方法计算他们的度为下表所示：

顶点	1	2	3	4	5
度	2	3	1	1	1

第 1 次执行，选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边：

将 1 和 3 的度分别减一：

顶点	1	2	3	4	5
度	1	3	0	1	1

第 2 次执行，选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边：

将 1 和 2 的度分别减一：

顶点	1	2	3	4	5
度	0	2	0	1	1

第 3 次执行，将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边：

将 2 和 4 的度分别减一：

顶点	1	2	3	4	5
度	0	1	0	0	1

最后，还剩下两个点 2 和 5 的度为 1，连边：

至此，一个 Purfer Sequence 得到的树画出来了，由上面的步骤可知，Purfer Sequence 和一个树唯一对应

综上，一个 Purfer Sequence 和一棵树一一对应

有了 Purfer Sequence 的知识，这题怎么搞定呢？

先不考虑无解的情况，从 Purfer Sequence 构造树的过程中可知，一个点的度数减一表示它在 Purfer Sequence 中出现了几次，那么：

假设度数有限制的点的数量为 cnt，他们的度数分别为：d[i]

另：

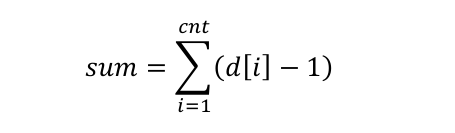
那么，在 Purfer Sequence 中的不同排列的总数为：

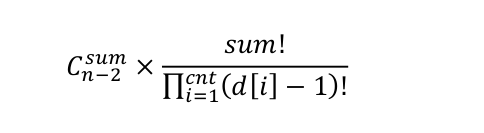
而剩下的 n-2-sum 个位置，可以随意的排列剩余的 n-cnt 个点，于是，总的方案数就应该是：

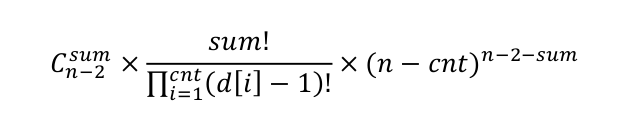
化简之后为：

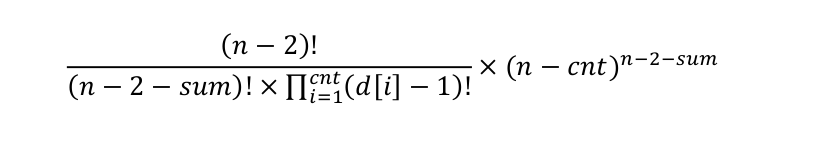
在有解的情况下，计算该结果输出就行了

无解的情况非常好确定，这里就再讨论了

参考代码

 import java.util.*;
 import java.math.*;

 public class Main {
     static int n, d[]=new int[10002];
     static BigInteger p[]=new BigInteger[1002];
     static BigInteger ans;

     static public void main(String args[]) {
         Scanner IN=new Scanner(System.in);
         n=IN.nextInt();
         int sum=0, flag=0, cnt=0;
         for(int i=0; i<n; i++) {
             d[i]=IN.nextInt();
             if(d[i]==0 || d[i]>n-1) flag=1;
             if(d[i]==-1) continue;
             sum+=d[i]-1;
             cnt++;
         }
         IN.close();
         if(n==1) {
             if(d[0]==0 || d[0]==-1) System.out.println(1);
             else System.out.println(0);
             return;
         }
         if(n==2) {
             if((d[0]==-1 || d[0]==1) && (d[1]==-1 || d[1]==-1)) System.out.println(1);
             else System.out.println(0);
             return;
         }
         if(flag==1) System.out.println(0);
         p[0]=BigInteger.ONE;
         for(int i=1; i<=n; i++) p[i]=p[i-1].multiply(BigInteger.valueOf(i));
         ans=p[n-2].divide(p[n-2-sum]);
         for(int i=0; i<n; i++) {
             if(d[i]==-1) continue;
             ans=ans.divide(p[d[i]-1]);
         }
         for(int i=0; i<n-2-sum; i++) ans=ans.multiply(BigInteger.valueOf(n-cnt));
         System.out.println(ans);
     }
 }

BZOJ 1005

题目链接 & AC 通道

BZOJ 1005 [HNOI2008] 明明的烦恼