Python机器学习/LogisticRegression（逻辑回归模型）（附源码）

LogisticRegression（逻辑回归）

逻辑回归虽然名称上带回归，但实际上它属于监督学习中的分类算法。

1.算法基础

LogisticRegression基本架构源自于Adline算法，只是在激励函数的选择上有所不同，Adline算法使用恒等函数作为激励函数，而Logistic选用sigmoid函数作为激励函数。

LogisticRegression算法的数学基础是两个函数：1）logit函数，2）极大似然函数；通过这两个函数构建了LR算法的基本框架。

1.1 logit函数

在概率问题中，有个比较重要的指标，机率比 ：

$\frac{p}{1-p}\\$

p代表二分类问题中正事件发生的概率。

在机率比的基础上延申出logit函数：

$logit(p) = log(\frac{p}{1-p})\\$

这里可以看出，p作为正事件发生的概率，取值范围为[0,1],logit(p)的取值范围是负无穷到正无穷。

将logit(p)与净输入值z关联，p作为数据数据正的概率，那么便有如下过程。

$logit(p) = z\\$

$log(\frac{p}{1-p})=z\\$

$\frac{p}{1-p} = e^{z}\\$

$\therefore p = \frac{1}{1+e^{-z}}\\$

$\frac{1}{1+e^{-z}}$被称为sigmod函数，这也就是为什么LR算法中采用sigmod函数作为激励函数的原因。

1.2极大似然函数

极大似然是概率论中估计值的一种，用于数据相互独立情况下最大概率出现的情况：

$L(w) = p(y|x;w) = \prod_{i=1}^{n}p(y^{(i)}|x^{(i)};w)\\$

$= \prod_{i=1}^{n}(\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{(1-y^{(i)})}\\$

对极大似然函数做对数处理会得到下面的公式：

$l(w) = \sum_{i=1}^{n} log(\phi(z^{(i)}))+(1-y^{(i)})log(1-\phi(z^{(i)}))\\$

将这个l(w)取负数得到的就是LR算法的损失函数。

2.算法框架

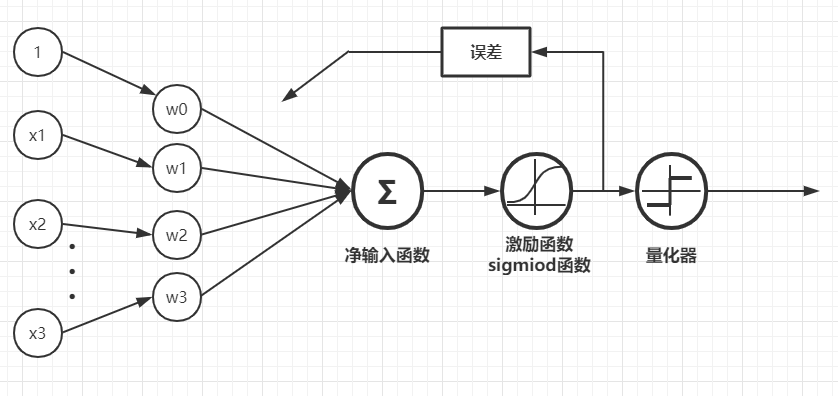
2.1净输入函数

$z = w_{0}x_{0} + w_{1}x_{1} + ··· +w_{n}x_{n}={\sum_{j=0}^{n}}w_{j}x_{j}=w^{T}x\\$

其中x0的值为1，用来和函数的偏移量相乘;在实际程序中可以使用两种方式实现净输入函数：

1）在训练数据X中添加值全部为1的列，作为偏移量的乘子；

2）将参数W中的偏移量w0单独提出来另算

用python实现，这里使用第二种方式

#净输入函数
def net_input(x,w):
    return np.dot(x,w[1:]) + w[0]

2.2激励函数

Logistic Regression与Adline算法的区别在于激励函数，Adline算法的激励函数是恒等函数，Logistic函数的激励函数时sigmoid函数。

$\phi (z) = \frac{1}{1+e^{-z}}\\$

2.3量化器

$ y=\left\{\begin{matrix}
1,\phi(z)\geq 0.5\\ 
-1,\phi(z)< 0.5
\end{matrix}\right. $

使用python实现量化器：

#量化器
def quantization(z):
    return np.where(z >= 0.5,1,-1)

3.损失函数

Logistic Regression算法的损失函数是由最大似然函数推导出来的，代价函数J的公式如下：

$J(w) = \sum_{i}^{n} -log(\phi(z^{(i)}))-(1-y^{(i)})log(1-\phi(z^{(i)})\\$

推导过程如下：

根据1.2节中的内容可知，最大似然函数为：

$L(w) = p(y|x;w) = \prod_{i=1}^{n}p(y^{(i)}|x^{(i)};w) = \prod_{i=1}^{n}(\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{(1-y^{(i)})}\\$

通过对极大似然函数做对数处理，得到

$l(w) = \sum_{i=1}^{n} log(\phi(z^{(i)}))+(1-y^{(i)})log(1-\phi(z^{(i)}))\\$

将极大似然函数对数取负，即是LogsticRegression的损失函数。

而我们的目标函数即最小化这个损失函数，即：

$min(l(w))\\$

4.优化算法

LR中的优化算法采用的是梯度下降法

$w:=w+\Delta w\\$

$\Delta w_{j} = -\eta \frac{\partial J}{\partial w_{j}} = \eta \sum_{i=1}^{n}(y^{(i)}-\phi(z^{(i)}))x_{j}^{(i)}\\$

5.正则化解决过拟合的问题

5.1正则化

过拟合是指一种现象：在训练集上表现良好，但在测试集上却性能不佳;一般导致过拟合的原因是因为算法过度拟合训练集上的数据，导致失去了泛化特性。

正则化是解决特征之间共线性（特征相关度高）的一个很有效的技术手段，它可以过滤掉数据中的噪声，最终防止过拟合。

最常用的正则化形式为L2正则化，可以写作：

$\frac{\lambda }{2}\sum_{j=1}^{m}w_{j}^{2}\\$

5.2正则化使用

一般是在代价函数中加上正则化函数，例如LogisticRegression算法中加入正则化后的代价函数为：

$J(w) = [\sum_{i}^{n} -log(\phi(z^{(i)}))-(1-y^{(i)})log(1-\phi(z^{(i)})]+\frac{\lambda }{2}\sum_{j=1}^{m}w_{j}^{2}$

在scikit-learn库中的LogisticRegression类的参数中，有个参数C，这个C表示的是正则化系数的倒数，即：

$C=\frac{1}{\lambda }$

6.使用scikit-learn库中的LogisticRegression类实现鸢尾花进行分类

源代码地址如下：

github地址