毕昇编译器优化：Lazy Code Motion

摘要：本文中，我们将介绍通过代码移动（插入）的方式消除冗余计算的一个典型方法。

本文分享自华为云社区《编译器优化那些事儿（3）：Lazy Code Motion》，作者：毕昇小助手。

导语

本文中，我们将介绍通过代码移动（插入）的方式消除冗余计算的一个典型方法。

下图给出的简要程序流图中， ①是我们想要优化的代码，②和③是优化后的代码，让我们先思考下面几个问题：

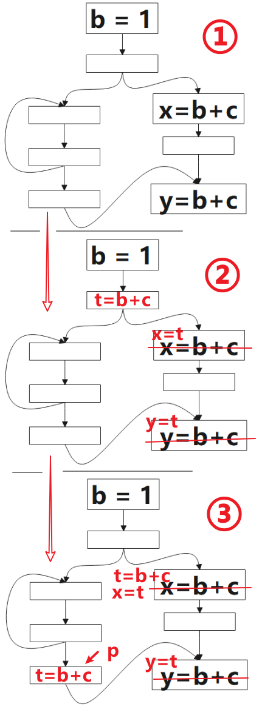
②和③哪个优化效果更好一点？

③ 更好一点，相比 ② 寄存器生存周期更短

③这种情况，在 p 点直接插入 t=b+c 会带来安全或性能问题吗? 会改变程序的行为吗?

这里不会引入冗余的计算，也没有改变程序行为。但如果 p 是下文介绍的非预期的点，我们就需要使用在临界边上增加合成块的方式避免这个问题了。

能否由编译器来完成一个算法，找到一个通用的、寻找到合适的插入点的方法以消除冗余计算？

这是本文要介绍的内容，我们会在下面算法章节引入四个定义，为程序在各个点上打上标签，通过这些点的集合之间的运算，得到插入点的集合。

0.1 开始之前

介绍算法之前，我们来看三个在写应用层代码时可能会遇到的问题。

（1）我们可以把计算移动到不会重复计算的路径吗？

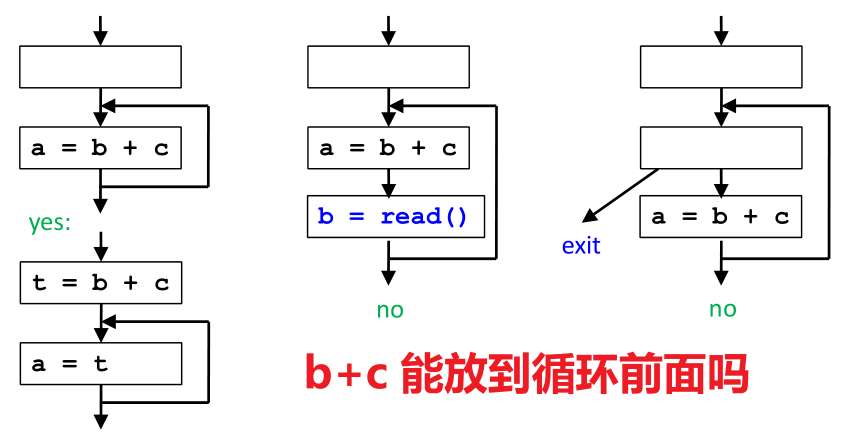
答案已在图中给出：

左边例子是可以的。这也是下文算法要找的情景。当然实际应用程序中会更复杂，以致我们不能明显看出或不经意间引入冗余的计算，比如《Lazy code motion》1 里给出的例子。
中间不可以，因为 b 被重新定义了，所以 a = b + c 不是冗余计算了。
右边不可以，因为 a = b + c 可能一次也没执行，移动到循环前可能会改变程序的行为。

（2）左图到右图的变化有优化效果吗

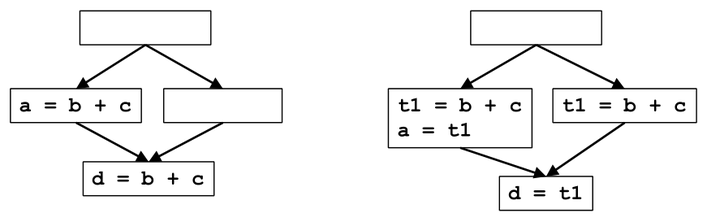
有的，这也是下面算法中要寻找的情景，左边的路径消除了一次冗余计算，右边为了保持程序正确性插入了一个计算，但并没有引入冗余的计算，所以总体是有优化的.

（3）下图中，能否在 block d 的父项 p 上插入表达式 t=b+c：

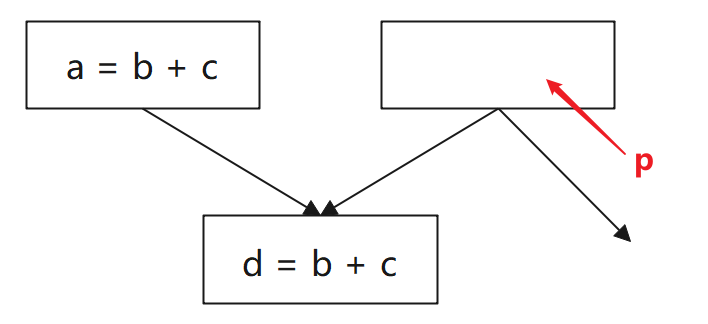
不能，因为插入不能改变程序的行为: 这里 t=b+c 可能难以看出问题，但如果表达式换成 b/c (c==0) 或 b^c 就能明显的看到造成了运行问题或性能问题。

解决方法：可在临界边(Critical Edge)上增加合成块(Synthetic Block)。

0.2 临界边(Critical Edge)的定义

定义：源基本块有多个后继，目标基本块有多个前驱，连接它们的边就叫临界边(Critical Edge)。

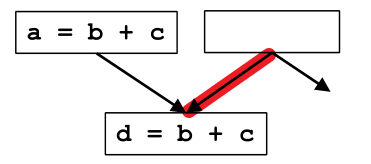
临界边如上图红色部分所示。

打破临界边(Critical Edge)的办法：增加合成块(Synthetic Block)

步骤：

为每个指向拥有多个前置的基本块添加一个基本块(不仅仅是在临界边上)。
为了保持算法简单，将每个语句视为其自己的基本块，并将指令的放置限制在基本块的开头。

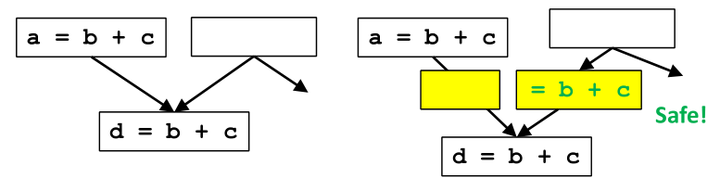
上图中我们插入了两个合成块，其中一个是多余的，但不用担心，我们可以在最后消除它。

1、算法

上文中，我们介绍了一个可以放心插入表达式而不会引入安全问题的方法，下面我们将正式介绍导语中提到的算法。

部分冗余消除算法要尽可能延迟计算，这也是标题中 lazy 的含义。

程序流程图如下：

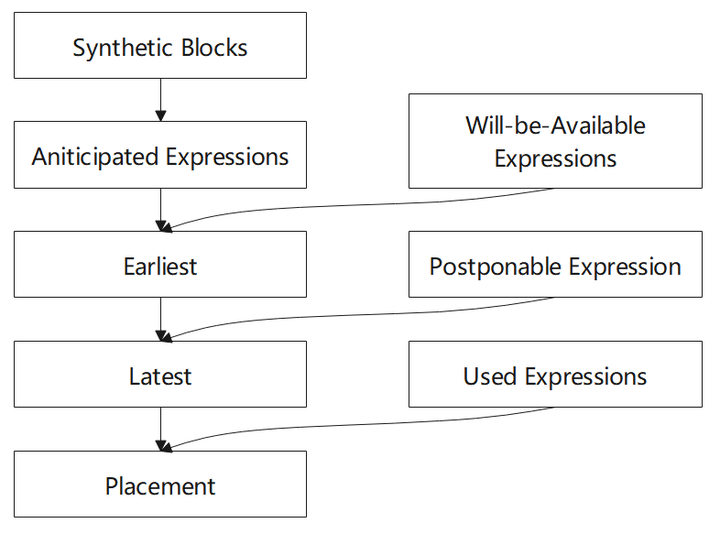
算法步骤：

首先计算预期表达式（Anticipated）集合
计算将可用的表达式（Will-be-Available）集合
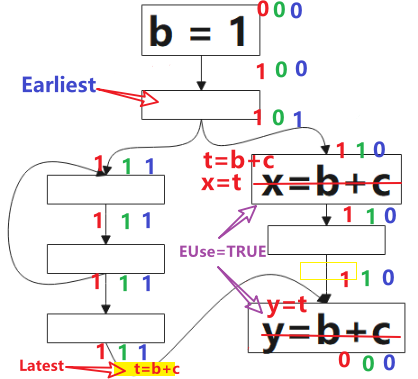
从 AVAIL 和 ANT ，我们为每个表达式计算出最早的插入位置（Earliest）集合，这最大限度地消除了冗余，但可能会增大寄存器生存期
再计算延迟表达式（Postponable）集合
经过上面的计算，引入 Latest 的定义，计算最晚插入的点的集合，实现与 earliest 相同数量的冗余消除，但缩短了保存表达式值的寄存器的生存期
计算使用表达式(Used)
计算最后的插入位置的集合，替换冗余表达式

我们会以下图为例，说明整个计算过程。根据以往的经验，下面给出的几个公式，必须结合图例去理解，文字无法阐述清楚准确定义。

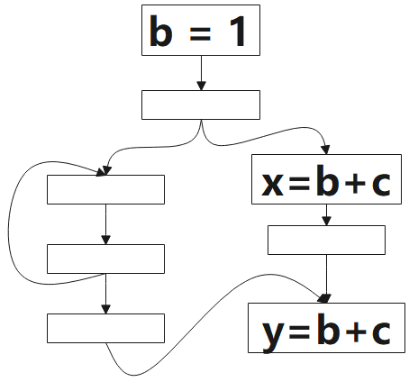
1.1 预期表达式（Anticipated）

Anticipated：An expression is said to be anticipated at program point if all paths leading from eventually computes (from the values of ’s operands that are available at ).

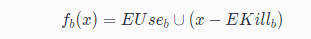
预期表达式（Anticipated）的分析方向为后向(backword)。

图示说明：

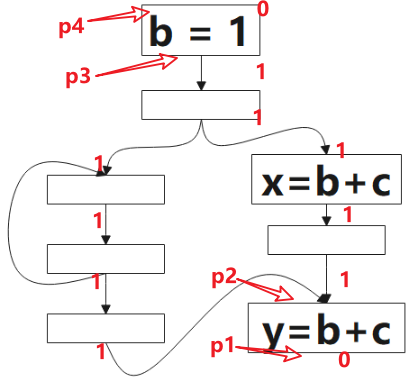
1 表示该点是可预期的（Anticipated），0 表示不是。该算法的方向是后向（backword）的，对应到图中，我们要从 p1 开始判断：对于表达式 b+c 而言，p1 是非预期的，因为到该点为止，没有 b+c 的计算，继续往上，看到了 b+c 的计算，所以 p2 点是可预期的（Anticipated），这情况一直持续到 p3，到 p4，由于该点看到了 b=1，b 被重新定义了，就是公式里被 Kill 的表达式，所以 p4 点不是可预期的（Anticipated）点。

1.2 将可用的表达式（Will-be-Available）

Will-be-available：An expression is said to be will-be-available at program point if it is anticipated and not subsequently killed along all paths reaching .

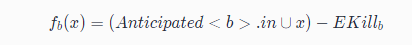
将可用的表达式（Will-be-Available）的分析方向为前向(forward)。

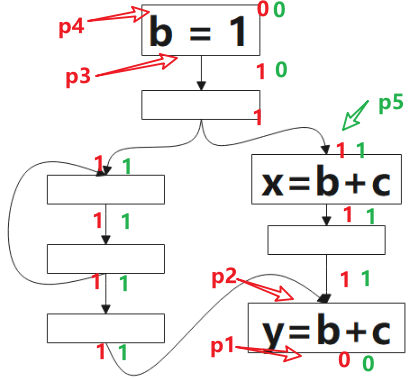
图中绿色的 1 表示表达式 b+c 该点是将可用的（Will-be-Available），0 表示不是。该算法方向是前向的，就是分析时，我们从 p4 开始看，根据公式的定义，该点不是可预期的（Anticipated），也没有计算表达式 b+c，所以该点不是将可用的（Will-be-Available），p3 虽然是可预期的（Anticipated），但因为 b=1 ，所以 p3 点对表达式 b+c 来说是 Ekillp ，所以该点仍不是将可用的，p5 点是可预期的（Anticipated），且该点没有 kill 的操作，该点是将可用的（Will-be-Available），后续的点类似。

接下来可以通过以下公式进行最早插入点的计算：

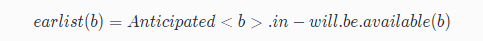
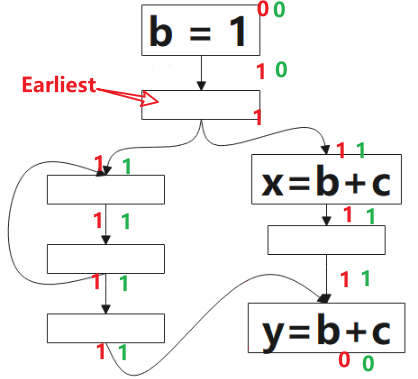
根据公式，最早可插入的点的集合是可预期点的(Anticipated)集合(图中红色1部分) 减去将可用点的(Will-be-Available)集合，得到图中标记的点。

目前为止我们已经找了一种通用的消除重复计算的方法，就是在上图中标注 Earliest 的点插入表达式 t=b+c, 然后在后面所有用到 b+c 的地方替换成 t，但这样做会带来一个问题，就是寄存器的生存期会很长。通过下一小节引入的定义，我们可以解决这个寄存器生存期的问题。

1.3 延缓表达式（Postponable）

An expression is said to be postponable at program point if all paths leading to have seen earliest placement of but not a subsequent use.

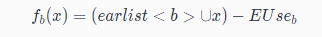
延缓表达式（Postponable）的分析方向为前向(forward)。

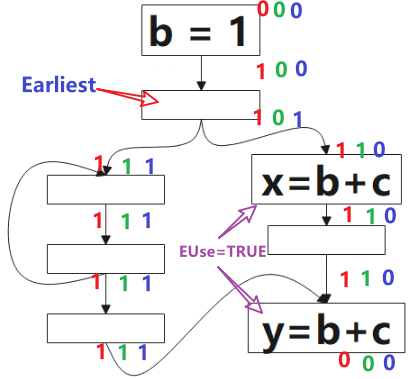
延迟创建冗余计算表达式可以减少寄存器压力：从公式看，Postponable点一定是在 Earliest 点的后面的，更接近表达式要被替换的地方，就是说，从表达式第一次被计算的点(结果在寄存器)到该结果被复用的点距离更近。

对于该图的讲解，可以参考 YouTube2 中的讲解。

接下来可以通过以下公式进行最晚插入点（Latest）的计算：

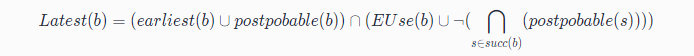
先在 Earliest 与 postpobable 集合的并集位置放置表达式 e 。
对上一步的点进行筛选，需要满足：表达式 e 在 b 点(随后的基本块)被Use 或它不是上一步点的后继。

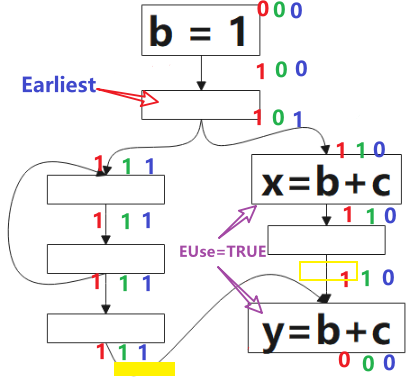
这里插入的点(图中黄色方块)是增加的合成块，是出于安全性的考虑。

1.4 已用表达式（Used Expressions）

An expression is said to be used at program point if there exists a path leading from that uses the expression before the operands are reevaluated.

已用表达式（Used Expressions）的分析方向为后向(backword)。

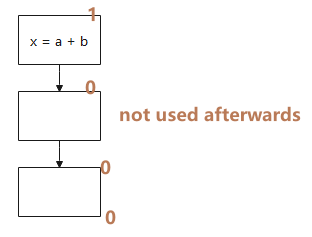
如图所示，从下往上看，未使用的点标记为0，直到使用的地方被标记为1。

引入这个定义主要是为了消除当前块之外未使用的临时变量赋值，计算方式： Used.out: sets of used (live) expressions at exit of b.

2、最终的解决方案

对所有的基本块/表达式 b，如果表达式属于最晚插入点的集合与已用点位置的交集，

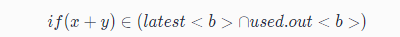
则在基本块b的开头，先创建 t = a + b，然后把所有的 x+y 替换为 t。

目前为止算法的介绍部分就已经全部讲完了，但是有些定义还是比较模糊，需要结合代码才能讲清楚, 大家可以翻看LLVM 源码3中关于该代码的具体实现： MachineCSE 类与 NaryReassociatePass 等类的实现。

参考

1.https://dl.acm.org/doi/abs/10.1145/143095.143136

2.https://www.youtube.com/watch?v=3s4oST3oZzQ&t=20s

3.https://github.com/llvm/llvm-project

点击关注，第一时间了解华为云新鲜技术~