算法 | 串匹配算法之KMP算法及其优化

主串　s：A B D A B C A B C

子串 ｔ:  A B C A B

问题：在主串 s 中是否存在一段 t 的子串呢？

形如上述问题，就是串匹配类问题。【串匹配——百度百科】

串匹配问题是一项有着非常多应用的重要技术，KMP匹配算法就是其中一种高效的字符串匹配算法。

在KMP算法之前先介绍一下BF算法，BF算法又名暴力匹配算法，该算法在匹配的时候把子串依次从主串的起始位置开始匹配，若匹配失败再从主串的下一个位置开始，子串重新从头开始匹配……

BF算法

int BF(char *str, char *sub)
{//暴力匹配算法
	int i = 0;	//遍历主串
	int j = 0;	//遍历子串
	int k = i;	//记录每次从主串匹配的起始位置
	while (i < strlen(str) && j < strlen(sub))
	{
		if (str[i] == sub[j])	//当前下标位置匹配
		{
			++i;
			++j;
		}
		else						//当前下标位置不匹配
		{
			if(strlen(str) - i <= strlen(sub) ) return -1;//优化，如果主串剩余的长度没有子串长，则肯定不匹配
			j = 0;		//子串从头开始匹配
			i = ++k;	//匹配失败，i从主串的下一位置开始
		}
	}
	if (j >= strlen(sub))	//子串遍历完，说明找到了对应的位置
	{
		return k;
	}
	else						//子串没有遍历完，说明无该子串
		return -1;
}

可以看到，BF算法是一种非常笨的算法，执行效率不高，那么有没有更优化的算法呢？

当然有啦，就是本文所讲的 KMP 算法。

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

KMP算法的核心在于求Next子串，Next子串也叫模式串的前缀表，也就是模式串的最长公共前后缀



GetNext

next 前缀表中存放着当前字符之前的串的最大公共前后缀。这样做的好处就在于，当模式串与主串进行匹配时，如果出现失配情况可以根据保存在 next 中的信息迅速定位，无需从头开始匹配。

比如：下列匹配情况

X X X X X A B A X X X

     A B A B C

A 与 C 不匹配，如果按照BF算法就要重头开始匹配了。但是我们发现，在模式串 A B A B C 中，有 A B 和 A B 相同的部分，那么是不是可以这样呢？

X X X X X A B A X X X

     A B A B C

         A B A B C

我们发现此时主串中的 A 与 模式串中的 A 匹配上了，先不管后续匹配情况如何，单就这个过程我们已经可以看出 KMP 算法的一些细节了。那么怎么让计算机实现我们上述的算法呢，这就不得不利用我们的next子串了。在本例中使用的以 -1，0 开头的next串格式，此格式便于在失配时（求next时失配或串匹配时失配） 快速回退。即 i = next(i) 这种形式。如下为求 next 的源码：

void GetNext(const char *sub, int *next)
{
	int len = strlen(sub);
	next[0] = -1;		//此前缀表从-1开始，一些书籍上是从0开始
	next[1] = 0;
	int i = 0;			//前缀
	int j = 1;			//后缀
	while(j < len-1)	//len-1 模式串中最后一个字符无需求前缀表
	{
		if (i == -1 || sub[i] == sub[j])	//匹配结束 || 匹配成功 ，写入next
		{
			next[++j] = ++i;
			//++i;
			//++j;
		}
		else			//匹配失败，i回退
		{
			i = next[i];
		}
	}
}

KMP匹配过程演示

//从主串pos位置开始查找，默认从头开始
int KMP(const char* str, const char* sub, int pos = 0 )
{
	int len_str = strlen(str);
	int len_sub = strlen(sub);

	if (pos < 0 || pos >= lenstr)	return -1;//位置非法，查找失败
	char* next = (char*)malloc(sizeof(char)*len_sub);	//构建前缀表
	GetNext(sub, next);

	int i = pos;	//主串	//从pos位置开始查找
	int k = 0;	//模式串/next
	while(i < len_str && k < len_sub)
	{
		if(k == -1 || str[i] == sub[k])	//k==-1匹配结束（失败）|| 匹配成功，向后移动
		{
			++k;++i;
		}
		else		//匹配失败，查询next表，移动模式串重新比较
		{
			k = next[k];
		}

	}

	free(next);

	if(k == len_sub)	//模式串遍历完，找到位置
	{
		return i-k;
	}
	else				//主串已结束，未找到子串
	{
		return -1;
	}

}

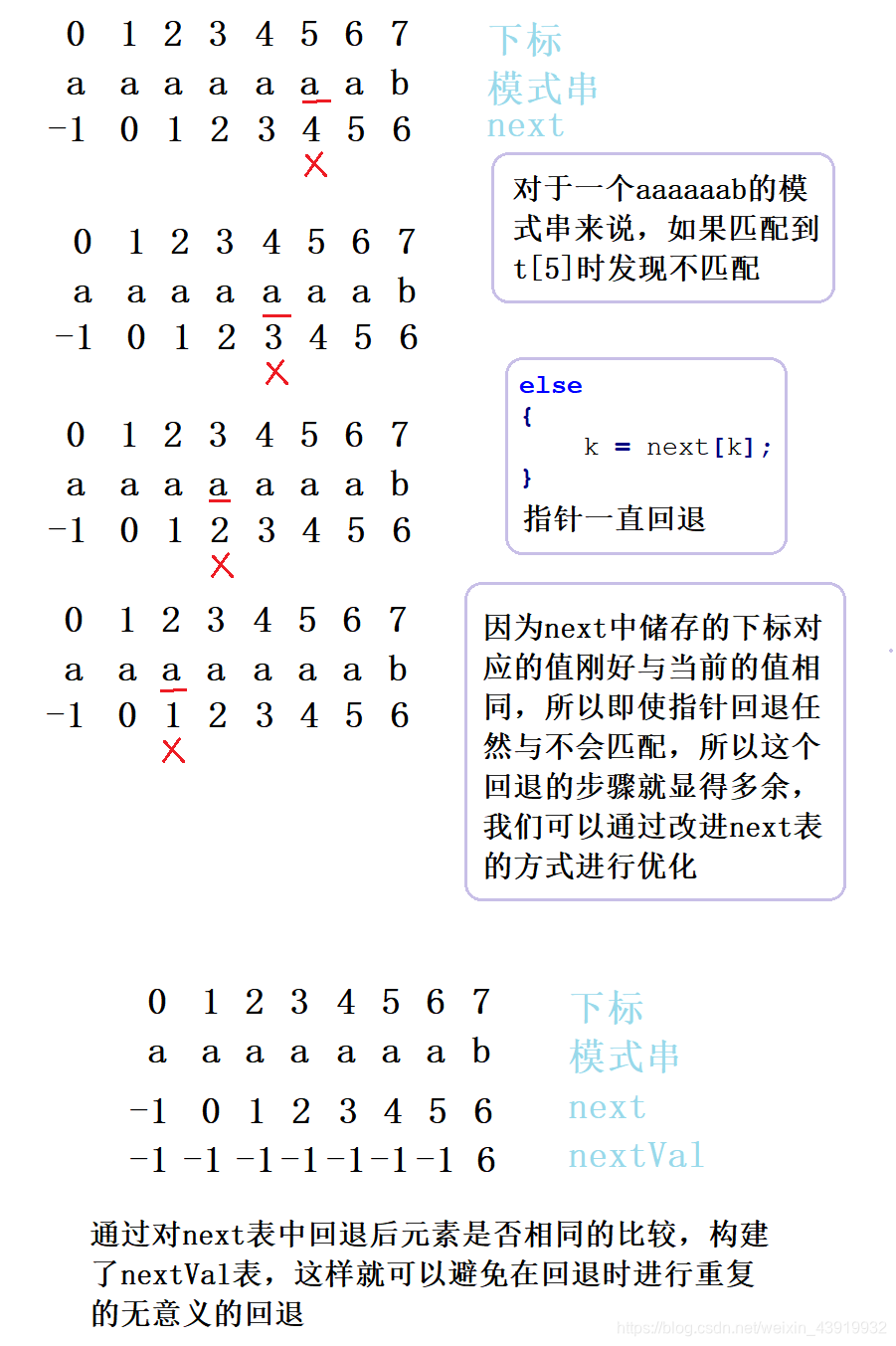
KMP算法的确是非常的智能，但是还有一种情况我们没有考虑到，比如一个 aaaaaaab 的模式串，在该模式串与主串匹配的时候，KMP算法也不是那么好用了。真是聪明难得糊涂一回，不过我们也有改进的方法，只需要去除next子串中多余重复的前缀并对其进行相应的优化即可，如下图所示：

优化：GetNextVal

void GetNextVal(const char* str, int* next)
{
	int len = strlen(str);
	next[0] = -1;
	next[1] = 0;
	int j = 1;
	int k = 0;

	while (j + 1 < len)
	{
		if (k == -1 || str[j] == str[k])
		{
			next[++j] = ++k;
		}
		else
		{
			k = next[k];
		}
	}

	int* nextval = (int*)malloc(len * sizeof(int));
	nextval[0] = -1;
	for (int i = 1; i < len; i++)
	{
		if (str[i] == str[next[i]])
		{
			nextval[i] = nextval[next[i]];
		}
		else
		{
			nextval[i] = next[i];
		}
	}

	for (int i = 0; i < len; i++)
	{
		next[i] = nextval[i];
	}
	free(nextval);
}