[0x11] 130.火车进站问题【卡特兰数】

题意

link（more：129.，P1044）

简化题意：给定严格从 \(1\thicksim n\) 这 \(n(n\leqslant 6\times10^4)\) 个整数，规定每个数都要进出栈各一次，求所有可能的出栈序列的数量。

这题有多种做法（爆搜，递推，dp，数学），最主要是 \(n\) 的范围，刚好会把像递推和 dp 这样的 \(O(n^2)\) 的次优化算法卡掉。

显然复杂度就要求是线性的，如此，可以使用组合数学中的 卡特兰数Catalan（link）。

理论推导

首先，我们以 \(n=3\) 为例，可以得到所有合法序列为： \(\{123,132,213,231,321\}\) 。

可以想到合法序列的数量就是 \(n\) 的全排列与其非法序列的差，但由此还无法得到非法序列的普遍特性，而影响它是否是合法序列的，无外乎就是 压入、弹出两个操作 。

那么我们可以具象化压入为 + ,弹出为 - ，可以得到对应的 +- 序列为：

\[\begin{cases}
123&+-+-+-
\\132&+-++--
\\213&++--+-
\\231&++-+--
\\321&+++---
\end{cases}\]

合法序列规律

观察可得：

• \(num(+)=num(-)=n\)；（注意：非法序列也可以）
• ∵在合法序列中，每一次弹出都与前面的一次压入是对应的，∴易得 \(\boxed{ sum_i\geqslant0(i\in[1,2n])}\) .（根据y总的说法，此乃 Catalan 的本质也）

非法序列规律

可能有的人和我一样，认为这里讨论的非法序列定义为：全排列中在栈中不可能存在的序列，但就是不存在，那我们也无法用 +- 序列表示出来。

那么，非法序列岂不是随便乱糊，可以有无数个了吗？

因此，我们必须在保证包括所有合法序列在其中的所有序列的集合中探求，形象地：

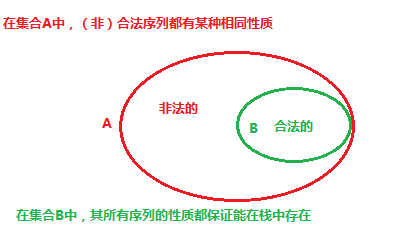
回到合法序列的两个规律中，显然非法序列就必须有两种性质：

• \(num(+)=num(-)=n\)；
• \(sum_i<0(i\in[1,2n]).\)

所有序列的组合数

诶，我们顺便可以得到所有序列的公式啦，∵不管合不合法，都保证了同一性质，相当于在 \(2n\) 个空位中插入 \(n\) 个 + 或 - ,即： \(\large C_{2n}^n\) .

---

格式有点乱，不要紧，继续探求非法序列。

我们在 平面直角坐标系 上对其进行进一步探究。（我们把 \(+,-\) 分别对应 \(x,y\) 作为一个单位的增量，且只能有这两种操作）

由于 \(num(+)=num(-)=n\) ，∴研究范围是 \((0,0)\) 到 \((n,n)\) ,可以建立 \(Oxy\) ，并随便把合法和非法的序列表示在上面：

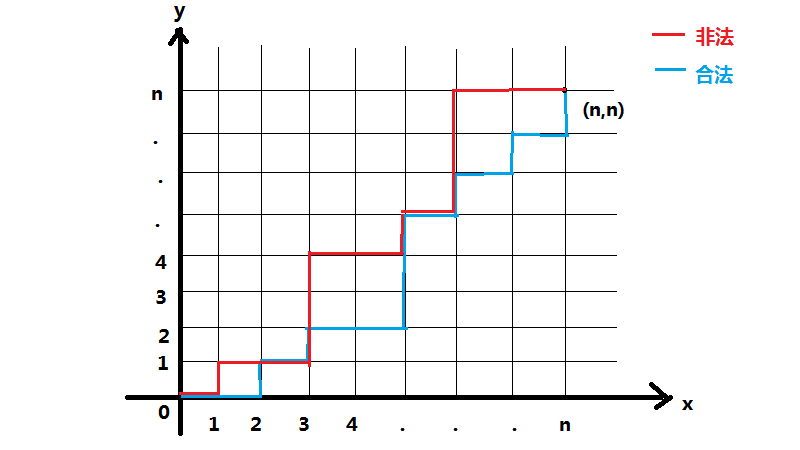
根据图像并结合先前的规律二，当在某一时刻 \(sum_i<0\) 时，则此时 \((x,y)\) 中 \(y>x\) ，总结易得，定义 \(y=x\) 为法线，当图像越过法线时，就为非法序列。

∵不好判断 越过 ，且合法路径也可以与法线有交点。

且 \(y>x\iff y\geqslant x+1\)

∴，当它越过法线就必然与 \(y=x+1\) 有交点，如图：

名字随便取着玩的

接下来这一步思想，可以说 前无古人，后无来者 了。

我们找到图中非法路径与高压法线的 第一个 交点，把交点后的原路径关于高压法线轴对称，与交点前的原路径形成一条从 \((0,0)\) 到 \((n-1,n+1)\) 的路径,如图：

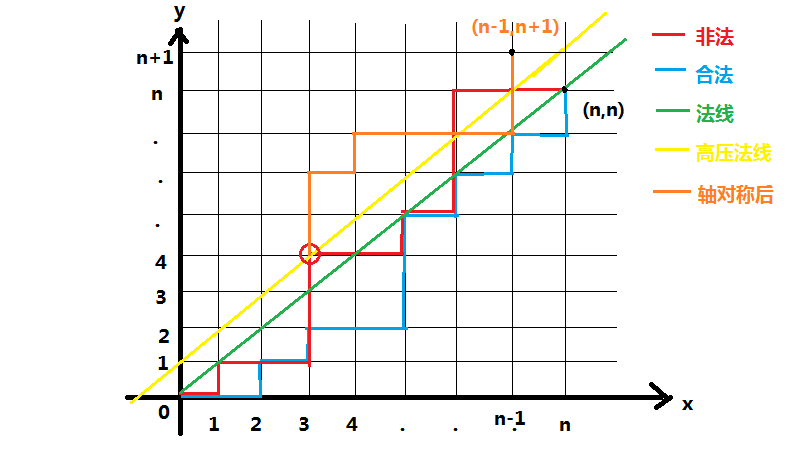
现在要开始转换了：(目的是将有条件限制的路径转换为无条件限制的路径)

我们把原路径叫做 \(A\) ，轴对称后的路径叫做 \(B\) .

在 \((0,0)\) 到 \((n,n)\) 中， \(A\) 是唯一的，且在 \((0,0)\) 到 \((n-1,n+1)\) 中， \(B\) 是唯一的， 且有且仅有 \(A\) 和 \(B\) 关于高压法线成轴对称；

∴ \(A\) 和 \(B\) 是一一对应的。

那么 非法路径的数量就等于从 \((0,0)\) 到 \((n-1,n+1)\) 的路径的数量 。

这下简单了，非法序列的数量等于该路径的数量，而该路径的数量，相当于走了 \((n-1)+(n+1)=2n\) 步，其中向右走了 \((n-1)\) 步、向上走了 \((n+1)\) 步，那么总数就为： \(\large C_{2n}^{n-1}\) 或 \(\large C_{2n}^{n+1}\) ，这两个显然是等价的：

\[C_{2n}^{n-1}=\frac{(2n)!}{[2n-(n-1)]!(n-1)!}=\frac{(2n)!}{(n+1)!(n-1)!}
\]

\[C_{2n}^{n+1}=\frac{(2n)!}{[2n-(n+1)]!(n+1)!}=\frac{(2n)!}{(n-1)!(n+1)!}
\]

合法序列的组合数

综上所述，可抽象为：

由分别 \(n\) 个 0 和 1 排成的，任意前缀和都 \(\geqslant 0\) 的序列的数量为：

\[C_{2n}^n-C_{2n}^{n-1}=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}=\frac{C_{2n}^n}{n+1}
\]

∴定义卡特兰数 \(\large Cat_n=\frac{C_{2n}^n}{n+1}\) .

此题思路

不知道要鸽多久，代码还没弄懂...