论文信息

论文标题：CGC: Contrastive Graph Clustering for Community Detection and Tracking
论文作者：Namyong Park, Ryan Rossi, Eunyee Koh, Iftikhar Ahamath Burhanuddin, Sungchul Kim, Fan Du, Nesreen Ahmed, Christos Faloutsos
论文来源：2022, AAAI
论文地址：download
论文代码：download

1 介绍

　　本文核心创新点：基于时间演化的聚类算法。2.2

　　创新点如下：

- 网络训练过程中的多层的表示矩阵可以视为多个视图 2.1.1 2.1.3
- 基于时间的表示交互 2.2.2
- 高阶结构（三角结构）的应用 2.1.1

　　和其他方法对比：

2 Method

2.1 CGC: Contrastive Graph Clustering

两个步骤：

refining cluster memberships based on the current node embeddings.
optimizing node embeddings such that nodes from the same cluster are closer to each other, while those from different clusters are pushed further away from each other.

2.1.1 Multi-Level Contrastive Learning Objective

　　正对：在同一个 cluster 中的节点。

　　负对：在不同的 cluster 中的节点。

Signal: Input Node Features

　　对于节点 $u$，将其输入特征 $\mathbf{f}_{u}$ 作为正样本，随机选择另一个节点 $v$，将其输入特征 $\mathbf{f}_{v}$ 作为负样本；然后将这些正负样本与节点嵌入 $\mathbf{h}_{u}$ 进行对比。

　　对于节点 $ u$ ，设 $\mathcal{S}_{u}^{F}=\left\{\mathbf{f}_{u}^{\prime i}\right\}_{i=0}^{r}$ 是包含一个正样本 $(i=0)$ 和 $r$ 个负样本（$1 \leq i \leq r$）（输入特征）的集合，其中 $\prime$ 表示采样。由于输入特征和节点嵌入可以有不同的维数，所以引入参数 $\mathbf{W}_{F} \in \mathbb{R}^{d^{\prime} \times d}$ 过渡，这里定义一个基于节点特征的对比损失$\mathcal{L}_{F}$：

　　　　${\large \mathcal{L}_{F}=\sum\limits _{u=1}^{n}-\log \frac{\exp \left(\left(\mathbf{h}_{u}^{\top} \mathbf{W}_{F} \mathbf{f}_{u}^{\prime 0}\right) / \tau\right)}{\sum_{v=0}^{r} \exp \left(\left(\mathbf{h}_{u}^{\top} \mathbf{W}_{F} \mathbf{f}_{u}^{\prime v}\right) / \tau\right)} } \quad\quad\quad(3)$

Signal: Network Homophily

　　设 $\mathcal{N}(u)$ 表示节点 $u$ 的邻居， $\mathcal{N}_{\Delta}(u)$ 既是节点 $u$ 的邻居也与节点 $u$ 在相同的三角结构（高阶结构）；因此，$\mathcal{N}_{\Delta}(u) \subseteq \mathcal{N}(u) $。

　　从 $\mathcal{N}(u)$ 中选择节点 $u$ 的一个正样本，选中 $\mathcal{N}_{\Delta}(u)$ 中的邻居的概率为 $\delta /\left|\mathcal{N}_{\Delta}(u)\right|$，其他邻居的概率为 $(1-\delta) /\left|\mathcal{N}(u) \backslash \mathcal{N}_{\Delta}(u)\right| $，其中 $\delta \geq 0$ 决定了 $\mathcal{N}_{\Delta}(u)$ 中节点的权重，最后从$\mathbf{H}=\mathcal{E}(G, \mathrm{~F})$ 中提取该正样本的节点嵌入 $\mathbf{h}_{u}^{\prime 0}$。

　　为构造负样本，设计了一个破坏函数 $C(G, \mathbf{F})$。具体来说，定义 $C(\cdot)$ 通过对 $\mathbf{F}$ 进行行变换（row-wise shuffling）返回损坏的节点特征矩阵$\widetilde{\mathbf{F}}$ ，同时保留图 $G$ 结构，即 $C(G, \mathbf{F})=(G, \widetilde{\mathbf{F}})$，可以看作是在保持图结构的同时在图上随机迁移节点。然后将GNN编码器应用于 $G$ 和 $\widetilde{\mathbf{F}}$ ，得到负节点嵌入 $\widetilde{\mathbf{H}} \in \mathbb{R}^{n \times d^{\prime}}$，并随机选择 $r$ 个负样本及其嵌入。

　　设 $\mathcal{S}_{u}^{H}=\left\{\mathbf{h}_{u}^{\prime i}\right\}_{i=0}^{r}$ 为包含节点 $u$ 的一个正样本（$i=0$）和 $r$ （ $1 \leq i \leq r$）个负样本嵌入的集合。在CGC中，基于同质性的对比损失 $\mathcal{L}_{H}$ 被定义为：

　　　　${\large \mathcal{L}_{H}=\sum\limits _{u=1}^{n}-\log \frac{\exp \left(\mathbf{h}_{u} \cdot \mathbf{h}_{u}^{\prime 0} / \tau\right)}{\sum_{v=0}^{r} \exp \left(\mathbf{h}_{u} \cdot \mathbf{h}_{u}^{\prime v} / \tau\right)}} \quad\quad\quad(4) $

Signal: Hierarchical Community Structure

　　设 $\mathcal{K}=\left\{k_{\ell}\right\}_{\ell=1}^{L}$ 为聚类数集合，$\mathrm{C}_{\ell} \in \mathbb{R}^{k_{\ell} \times d^{\prime}}$ 为第 $\ell$ 个聚类质心矩阵。给定嵌入矩阵 $\mathbf{H}$ 和簇质心矩阵 $\left\{\mathrm{C}_{\ell}\right\}_{\ell=1}^{L} $。节点 $u$ 的正样本为节点 $u$ 最相近的 $L$ 个簇质心。而其负样本是从第 $\ell$ 个其他 $k_{\ell}-1$ 聚类质心中随机选择的。

　　设 $\mathcal{S}_{u, \ell}^{C}=\left\{\mathbf{c}_{u, \ell}^{i}\right\}_{i=0}^{r_{\ell}}$ 为包含节点 $u$ 的一个正样本（$i=0$）和 $r_{\ell}$ 个负样本（$1 \leq i \leq r_{\ell}$）（即质心）嵌入在 $k_{\ell}$ 质心中选择的节点。CGC定义了一个基于社区的分层对比损失 $\mathcal{L}_{C}$ 为：

　　　　${\large \mathcal{L}_{C}=\sum\limits _{u=1}^{n}-\left(\frac{1}{L} \sum\limits_{\ell=1}^{L} \log \frac{\exp \left(\mathbf{h}_{u} \cdot \mathbf{c}_{u, \ell}^{\prime 0} / \tau\right)}{\sum\limits_{v=0}^{r_{\ell}} \exp \left(\mathbf{h}_{u} \cdot \mathbf{c}_{u, \ell}^{v} / \tau\right)}\right)}\quad\quad\quad(5) $

Multi-Level Contrastive Learning Objective

　　多层次的对比性学习目标。上述损失项在多个层次上捕获社区结构上的信号，即单个节点特征$\left(\mathcal{L}_{F}\right)$、相邻节点 $\left(\mathcal{L}_{H}\right)$ 和分层结构的社区 $\left(\mathcal{L}_{C}\right)$。CGC联合优化

　　　　$\mathcal{L}=\lambda_{F} \mathcal{L}_{F}+\lambda_{H} \mathcal{L}_{H}+\lambda_{C} \mathcal{L}_{C}\quad\quad\quad(6)$

　　其中，$\lambda_{F} $、$\lambda_{H} $、$\lambda_{C}$ 是损失项的权重。

2.1.2 Encoder Architecture

　　作为我们的节点编码器 $\mathcal{E}$，我们使用一个带有平均聚合器的 GNN：

　　　　$\mathbf{h}_{v}^{l}=\operatorname{ReLU}\left(\mathbf{W}_{G} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{l-1}\right\} \cup\left\{\mathbf{h}_{u}^{l-1} \mid \forall u \in \mathcal{N}(v)\right\}\right)\right)\quad\quad\quad(7)$

2.1.3 Algorithm

　　算法如下：

　　其中：

- $\Pi$ 代表着聚类算法，如 $k -means$；　　
- $ \left\{\Phi_{\ell}\right\}$ 代表着聚类分配矩阵；

2.2 CGC for Temporal Graph Clustering

　　小结导读：后面 2.2.3 会用。

　　给定时间图流（ temporal graph stream）$\mathcal{G}= \left\{G_{\tau_{1}}, \ldots, G_{\tau_{i-1}}\right\}$ （其中 $G_{\tau_{i}}$ 是其中的一个图快照），学习到的节点嵌入矩阵 $\mathbf{H}_{i-1}$ 和聚类分配矩阵 $\Phi_{i-1}$ 基于直到 $i-1$ 之前的图快照（ snapshot）。$\mathbf{H}_{i-1}$ 和 $\Phi_{i-1}$ 用于反应 $G_{\tau_{i}}$ 中的新信息。

　　为方便，这里记 $G_{i: j} $ 表示 $ i $ 到 $j$ 的图快照集合，即 $\left\{G_{\tau_{i}}, \ldots, G_{\tau_{j}}\right\} $，其中 $ G_{i: j}=\left(V, E_{i: j}\right)$，$E_{i: j}=\bigcup_{o=i}^{j} E_{\tau_{o}}$ 。

　　下面将描述如何扩展 CGC 用于时间图聚类。

2.2.1 Temporal Contrastive Learning Objective

　　学习表示时，表示一般都是平稳变化。因此，在一个时间跨度范围内观察到的节点的边提供了相似或相关的时间视图。

　　给定时间戳 $j$ 和节点 $u$ ，我们将时间戳 $j-1 $ 时的嵌入 $\mathbf{h}_{u, j-1}$ 作为其正样本。

　　为获得负样本，使用 2.1.1节中使用的破坏函数，得损坏节点特征矩阵 $\widetilde{\mathbf{F}}$，使用 $\mathcal{E}\left(G_{i: j-1}, \widetilde{\mathbf{F}}\right)$ 并视节点 $u$ 对应的嵌入作为负样本（这里的 $u $ 其实不是节点 $u$ ，只是位置对应其他节点 $v$）。打乱多次特征矩阵 $\widetilde{\mathbf{F}}$ ，重复上述过程，便可以得到多组负样本。【个人觉得完全有点多此一举，反正都是负样本还不如直接随机选取 $r$ 个样本】

　　设 $\mathcal{S}_{u, j}^{T}=\left\{\mathbf{h}_{u, j-1}^{\prime i}\right\}_{i=0}^{r}$ 包含节点 $u$ 的一个正样本（$i=0$）和 $r$ 个负样本（$1 \leq i \leq r$）。CGC定义了一个在时间 $j$ 的对比损失 $\mathcal{L}_{T}$ ：

　　　　${\large \mathcal{L}_{T}=\sum\limits _{u=1}^{n}-\log \frac{\exp \left(\mathbf{h}_{u, j} \cdot \mathbf{h}_{u, j-1}^{\prime 0} / \tau\right)}{\sum\limits_{v=0}^{r} \exp \left(\mathbf{h}_{u, j} \cdot \mathbf{h}_{u, j-1}^{\prime v} / \tau\right)}} \quad\quad\quad(8)$

　　请注意，$\text{Eq.8}$ 与第 2.1.1 节中讨论的目标相结合，其权重为$\lambda_{T}$，将损失 $\mathcal{L}$ 增加为

　　　　$\mathcal{L}=\lambda_{F} \mathcal{L}_{F}+\lambda_{H} \mathcal{L}_{H}+\lambda_{C} \mathcal{L}_{C}+\lambda_{T} \mathcal{L}_{T}\quad\quad\quad(9)$

2.2.2 Encoder Architecture

　　对 GNN 编码器进行扩展：使得节点给予最近与该节点交互的邻居更多权重，所以需要根据邻居最近交互的时间来调整邻居权重。

　　设 $t_{(u, v)} $ 表示节点 $u$ 和 $v$ 之间边的时间戳，并设 $t_{v}^{\max }= \underset{u \in \mathcal{N}(v)}{\text{max}}\;\;\; \left\{t_{(u, v)}\right\}$，即节点 $v$ 与其邻居交互时的最新时间戳。$\psi\in [0,1]$ 表示时间衰减因子，我们将时间衰减应用于邻域 $u$ 的嵌入 $\mathbf{h}_{u}$ 如下：

　　　　${\large \operatorname{td}\left(\mathbf{h}_{u}\right)=\psi^{t_{v}^{\max }-t_{(u, v)}} \mathbf{h}_{u}} \quad\quad\quad(10)$

　　然后对于具有时间感知能力的邻域聚合，将 $\text{Eq.7}$ 中的 $\mathbf{h}_{u}$ 替换为其时间衰减版本 $\operatorname{td}\left(\mathbf{h}_{u}\right) $。

2.2.3 Graph Stream Segmentation

　　合并之前的快照生成新快照是基于前后的相似性假设，然而在训练时网络可能产生突变，导致新的快照在某种程度上和之前并不一致，所以需要检测这些变化。

　　设 $\mathcal{G}_{\text {seg }}=\left\{G_{\tau_{i}}, \ldots, G_{\tau_{j}}\right\}$ 是 $i$ 到 $j$ ($i<j$) 之间的图流段（graph stream segment）。给定一个快照 $G_{\tau_{j+1}}$ ，如果 $G_{\tau_{j+1}}$ 与 $\mathcal{G}_{\text {seg }}$ 相似，我们使用 $G_{\tau_{j+1}}$ 扩展当前段 $\mathcal{G}_{\text {seg }}$ ；如果不相似，将启动一个只由 $G_{\tau_{j+1}}$ 组成的新的图流段。【该问题为流式图分割问题】

　　解决这个问题的想法是比较出现在 $\mathcal{G}_{\text {seg }}$ 和 $G_{\tau_{j+1}}$ 两者中的节点嵌入。

　　这一步的 GNN 编码器已经基于 $\mathcal{G}_{\text {seg }}$ 训练好了，但并没有在 $G_{\tau_{j+1}}$ 训练。如果 $\mathcal{G}_{\text {seg }}$ 和 $G_{\tau_{j+1}}$ 相似，他们对应的表示也相似。那么接下来分析 $G_{\tau_{j+1}}$ 与 $\mathcal{G}_{\text {seg. }}$ 不相似的情况。

　　设 $V^{*}$ 表示同时出现在 $\mathcal{G}_{\text {seg }} $ 和 $G_{\tau_{j+1}} $ 之中的节点集合，设 $\mathbf{H}_{V^{*}}^{\text {seg }}, \mathbf{H}_{V^{*}}^{j+1} \in \mathbb{R}^{\left|V^{*}\right| \times d^{\prime}} $ 分别表示 $V^{*}$ 基于 $\mathcal{G}_{\text {seg }}$、$G_{\tau_{j+1}}$ 的表示。这里定义距离度量函数 $ d(\cdot, \cdot)$（cosine distance），$\mathrm{H}_{V^{*}}^{\mathrm{seg}} $ 和 $\mathbf{H}_{V^{*}}^{j+1}$ 之间的距离 $Dist (\cdot, \cdot)$ 定义为：

　　　　$\operatorname{Dist}\left(\mathbf{H}_{V^{*}}^{\operatorname{seg}}, \mathbf{H}_{V^{*}}^{t+1}\right)=\operatorname{MEAN}\left\{d\left(\left(\mathbf{H}_{V^{*}}^{\operatorname{seg}}\right)_{i},\left(\mathbf{H}_{V^{*}}^{t+1}\right)_{i}\right) \mid i \in V^{*}\right\}\quad\quad\quad(11)$

　　如果距离超过了一个阈值，则对流进行分段。

　　GraphStreamSegmentation 算法如下：

2.2.4 Putting Things Together

　　CGC在一个增量的端到端框架(Alg. 2).当一个新的图形快照到达时，CGC使用 Alg. 3 (line 3) 自适应地确定一个要从中查找簇的图形快照序列，并使用 Alg. 1 (line 4) 更新聚类结果和节点嵌入。

3 Experiments

数据集

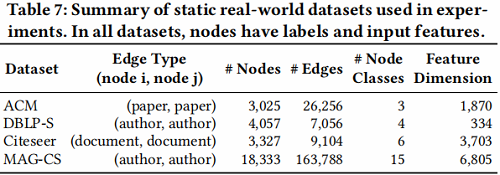
基线实验

论文解读（CGC）《CGC: Contrastive Graph Clustering for Community Detection and Tracking》