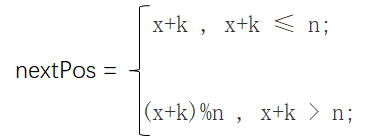UVA 133“The Dole Queue”(循环报数处理技巧)
•参考资料
[1]:紫书P82
•题意(by紫书)
按照被选中的次序输出这 n 个人的编号;
如果A和B选中的是同一个人,输出一个这个人的编号;
输出格式:输出的每个编号占3个字节,不够3个字节在前面用空格补;
•循环报数处理技巧
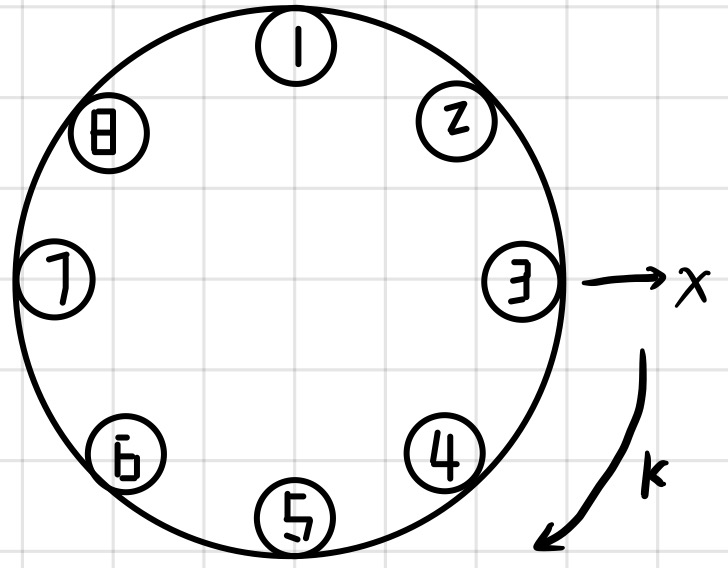
n个人按照逆时针顺序编号1~n;
给你一个整数 k 和 cur;
cur表示从这 n 个人中任意选取的一个编号;
k > 0 : 找 cur 左手边的第 k 个人的编号;
k < 0 : 找 cur 右手边的第 k 个人的编号;
循环报数问题,需要处理的边界问题是:
编号 1 的左手边的人的编号为 n;
编号 n 的右手边的人的编号为 1;
之前常用的处理的方式为,循环处理,如果 cur 从编号 n 来到编号 n+1,特判,令其等于 1;
反之,如果 cur 从编号 1 来到编号 0,特判,令其等于 n;
下面说下一我从紫书上学到的技巧;
1 pos = (cur + k - 1 + n)%n + 1;
pos : 从cur编号顺时针或逆时针找到的第k个人的编号
k : k > ,找cur右手边的第k个人的编号,反之找cur左手边的第k个人的编号;while(~scanf("%d%d%d",&n,&cur,&k))
{
k=k%n;
int pos=(cur+k-1+n)%n+1;
cout<<pos<<endl;
}•我的理解
n个人顺时针围城一圈,从 x 位置开始,顺时针找其左(或逆时针找其右)手边的第 k 个人(-n < k < n , k > 0 顺时针找, k < 0 逆时针找);
假设 k > 0 ,那么第 k 个人的编号为:
合并这两个式子就是
nextPos = (x+k-1+n)%n+1;
简单证明这个式子得正确性:
①如果 x+k ≤ n,那么 (x+k-1+n)%n+1 = x+k;
②如果 x+k > n:
1)x+k = n+1 : (x+k-1+n)%n+1 = 1;
2)x+k > n+1 : (x+k-1+n)%n 就是目的编号的前一个编号,+1就等于目的编号;
那如果 k < 0 呢?
假设找 x 左手边的第 y 个人的编号 = 找 x 右手边的第 k 个人的编号;
那么 |k| + y = n,也就是 y = n-|k|;
带入上式得:
nextPos = (x+n-|k|-1+n)%n+1;
即 nextPos = (x-|k|-1+n)%n+1;
综上,不论 k 是大于0还是小于0,nextPos = (x+k-1+n)%n+1;
•Code
#include<bits/stdc++.h>
using namespace std;
#define memF(a,b,n) for(int i=0;i <= n;a[i++]=b); int n,k,m;
bool vis[]; int Go(int cur,int d,int x)
{
/**
d=1:逆时针找第x个人
d=-1:顺时针找第x个人
当前的cur肯定是不满足条件的位置
所以初始 a=n,b=1
之后,a,b的值就是上一次出队的编号
*/
while(x--)
{
do
{
cur=(cur+d-+n)%n+;
}while(vis[cur]);
}
return cur;
}
void Solve()
{
memF(vis,false,n); int a=n,b=;
int left=n;
while(left--)
{
a=Go(a,,k);
b=Go(b,-,m); vis[a]=true;
vis[b]=true; printf("%3d",a);
if(b != a)
{
left--;
printf("%3d",b);
}
if(left)
printf(",");
}
printf("\n");
}
int main()
{
while(~scanf("%d%d%d",&n,&k,&m) && n+k+m)
Solve(); return ;
}
UVA 133“The Dole Queue”(循环报数处理技巧)的更多相关文章
- UVA 133 The Dole Queue
The Dole Queue 题解: 这里写一个走多少步,返回位置的函数真的很重要,并且,把顺时针和逆时针写到了一起,也真的很厉害,需要学习 代码: #include<stdio.h> # ...
- uva - 133 The Dole Queue(成环状态下的循环走步方法)
类型:循环走步 #include <iostream> #include <sstream> #include <cstdio> #include <cstr ...
- UVA 133 The Dole Queue(报数问题)
题意:一个长度为N的循环队列,一个人从1号开始逆时针开始数数,第K个出列,一个人从第N个人开始顺时针数数,第M个出列,选到的两个人要同时出列(以不影响另一个人数数),选到同一个人就那个人出列. 思路: ...
- uva 133 The Dole Queue 双向约瑟夫环 模拟实现
双向约瑟夫环. 数据规模只有20,模拟掉了.(其实公式我还是不太会推,有空得看看) 值得注意的是两个方向找值不是找到一个去掉一个,而是找到后同时去掉. 还有输出也很坑爹! 在这里不得不抱怨下Uva的o ...
- uva 133(The Dole Queue UVA - 133)
一道比较难想的模拟题,用了队列等东西,发现还是挺难做的,索性直接看了刘汝佳的代码,发现还是刘汝佳厉害! 代码本身难度并不是很大,主要还是p=(p+n+d-1)%n+1;这一句有些难度,实际上经过自己的 ...
- uvaoj 133 - The Dole Queue(逻辑,环形队列数数)
https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- UVa133.The Dole Queue
题目链接:http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- The Dole Queue UVA - 133
In a serious attempt to downsize (reduce) the dole queue, The New National Green Labour Rhinoceros ...
- The Dole Queue
The Dole Queue Time Limit:3000MS Memory Limit:0KB 64bit IO Format:%lld & %llu Submit cid ...
随机推荐
- 移动Web应用程序开发HTML5篇
https://software.intel.com/zh-cn/blogs/2012/03/09/webhtml5-offline-web-applications
- leetcode 【 Find Peak Element 】python 实现
题目: A peak element is an element that is greater than its neighbors. Given an input array where num[ ...
- XMind8 Pro激活
最近使用XMind8 还不错,奈何更多功能是需要升级8Pro才能使用,现已经激活成功,记录下过程: 1.下载XMind8 Update4并且安装,此安装过程简单[安装包太大,无法上传,正在想办法] 2 ...
- linux/mac下的配置自定义命令alias
linux/mac下的自定义命令alias,并保存别名使其永久生效(重启不会失效) 在做开发每次提交代码的命令都是一长串参数,不想去记,于是可以使用alias命令来解决这个问题:alias aComm ...
- Docker Hadoop LAMP安装配置教程
以下教程来自九章算法. 1.How to install Dockerhttps://bupt.quip.com/YehSAR4qnGqB 2.How to set up hadoop environ ...
- [oldboy-django][2深入django]Form组件实现生成: select下拉框, checkbox复选框,radio单选框以及如何实现自定义数据格式要求
1 需求 - 1Form组件如何实现生成选择类标签: select,check, radio - 默认值 - 保留上次输入的值 - 2自定义验证规则 - RegexField - -
- cf 853 D Michael and Charging Stations [dp]
题面: 传送门 思路: 看到题目,第一思路是贪心,但是我很快就否决掉了(其实分类贪心也可以做) 然后就想,贪心不能解决的状态缺失,是否可以用dp来解决呢? 事实证明是可以的 我们设dp[i][j]表示 ...
- ionic2 jpush
ionic2 为ionic2调用极光插件提供符合angular2及TS的调用方式 install 先安装官方的cordova插件 $ cordova plugin add jpush-phonegap ...
- 【Codeforces Round #518 (Div. 2)】
A:https://www.cnblogs.com/myx12345/p/9847588.html B:https://www.cnblogs.com/myx12345/p/9847590.html ...
- EnableViewState 属性
原文发布时间为:2009-10-25 -- 来源于本人的百度文章 [由搬家工具导入] 指示是否在页请求之间保持视图状态。如果要保持视图状态,则为 true;否则为 false。默认值为 true。 自 ...