【bzoj3944/bzoj4805】Sum/欧拉函数求和 杜教筛

bzoj3944

题目描述

输入

一共T+1行

第1行为数据组数T(T<=10)

第2~T+1行每行一个非负整数N，代表一组询问

输出

一共T行，每行两个用空格分隔的数ans1,ans2

样例输入

6
1
2
8
13
30
2333

样例输出

1 1
2 0
22 -2
58 -3
278 -3
1655470 2

bzoj4805

同上，不需要求mu

---

题解

杜教筛

公式推导：

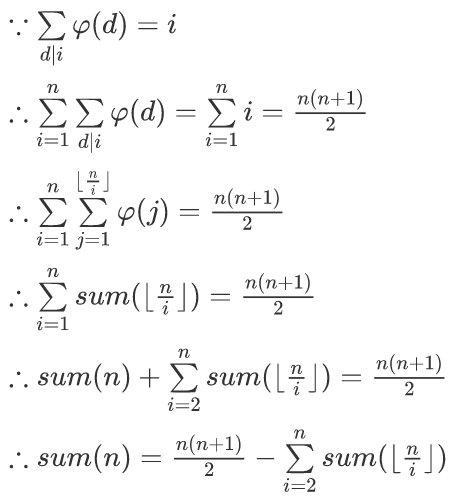
这里有一个难点（其实也不能算难），就是由枚举d|i到枚举j≤⌊n/i⌋。此时可以看作下面语句的i是上面语句的i/d，而下面语句的j就是上面语句的d。这样枚举的话，不会出现重复或遗漏，不会超过n，并且便于计算。

推出这个式子之后，枚举⌊n/i⌋的取值（最多只有√n种），用记忆化搜索的方法记录每次的sum(⌊n/i⌋)，并累计到sum(n)中。这里需要使用map。

这样做的时间复杂度是O(n^3/4logn)，如果预处理出n^2/3以内的phi值，就能使时间复杂度达到更小的O(n^2/3logn)。

这样就解决了bzoj4805。对于bzoj3944还需要求莫比乌斯函数的前缀和，方法和欧拉函数非常类似，运用到了∑mu(d)(d|n)=1的性质，只需要把n(n+1)/2换成1即可。

bzoj3944：

#include <cstdio>
#include <map>
#include <utility>
#define N 3000010
using namespace std;
typedef long long ll;
map<ll , pair<ll , ll> > f;
map<ll , pair<ll , ll> >::iterator it;
ll phi[N] , mu[N] , prime[N] , tot , sumphi[N] , summu[N] , m = 3000000;
bool np[N];
void query(ll n , ll &ans1 , ll &ans2)
{
    if(n <= m)
    {
        ans1 = sumphi[n] , ans2 = summu[n];
        return;
    }
    it = f.find(n);
    if(it != f.end())
    {
        ans1 = it->second.first , ans2 = it->second.second;
        return;
    }
    ans1 = n * (n + 1) / 2 , ans2 = 1;
    ll i , last , tmp1 , tmp2;
    for(i = 2 ; i <= n ; i = last + 1)
    {
        last = n / (n / i) , query(n / i , tmp1 , tmp2);
        ans1 -= (last - i + 1) * tmp1 , ans2 -= (last - i + 1) * tmp2;
    }
    f[n] = make_pair(ans1 , ans2);
}
int main()
{
    int T;
    ll n , i , j , ans1 , ans2;
    np[1] = 1 , mu[1] = phi[1] = sumphi[1] = summu[1] = 1;
    for(i = 2 ; i <= m ; i ++ )
    {
        if(!np[i]) prime[++tot] = i , phi[i] = i - 1 , mu[i] = -1;
        for(j = 1 ; j <= tot && i * prime[j] <= m ; j ++ )
        {
            np[i * prime[j]] = 1;
            if(i % prime[j] == 0)
            {
                phi[i * prime[j]] = phi[i] * prime[j] , mu[i * prime[j]] = 0;
                break;
            }
            else phi[i * prime[j]] = phi[i] * (prime[j] - 1) , mu[i * prime[j]] = -mu[i];
        }
        sumphi[i] = sumphi[i - 1] + phi[i] , summu[i] = summu[i - 1] + mu[i];
    }
    scanf("%d" , &T);
    while(T -- ) scanf("%lld" , &n) , query(n , ans1 , ans2) , printf("%lld %lld\n" , ans1 , ans2);
    return 0;
}

bzoj4805：

#include <cstdio>
#include <map>
#define N 1600010
using namespace std;
typedef long long ll;
map<ll , ll> f;
map<ll , ll>::iterator it;
ll m = 1600000 , phi[N] , prime[N] , tot , sum[N];
bool np[N];
ll query(ll n)
{
    if(n <= m) return sum[n];
    it = f.find(n);
    if(it != f.end()) return it->second;
    ll ans = n * (n + 1) / 2 , i , last;
    for(i = 2 ; i <= n ; i = last + 1) last = n / (n / i) , ans -= (last - i + 1) * query(n / i);
    f[n] = ans;
    return ans;
}
int main()
{
    ll i , j , n;
    phi[1] = sum[1] = 1;
    for(i = 2 ; i <= m ; i ++ )
    {
        if(!np[i]) phi[i] = i - 1 , prime[++tot] = i;
        for(j = 1 ; j <= tot && i * prime[j] <= m ; j ++ )
        {
            np[i * prime[j]] = 1;
            if(i % prime[j] == 0)
            {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
        sum[i] = sum[i - 1] + phi[i];
    }
    scanf("%lld" , &n);
    printf("%lld\n" , query(n));
    return 0;
}