【特征匹配】SIFT原理与C源代码剖析

相关： KD树+BBF算法解析

SURF原理与源代码解析

SIFT的原理已经有非常多大牛的博客上做了解析，本文重点将以Rob Hess等人用C实现的代码做解析，结合代码SIFT原理会更easy理解。一些难理解点的用了☆标注。

欢迎大家批评指正。

转载请注明出处：http://blog.csdn.net/luoshixian099/article/details/47377611

SIFT（Scale-invariant feature transform）即尺度不变特征转换，提取的局部特征点具有尺度不变性，且对于旋转。亮度，噪声等有非常高的稳定性。

下图中，涉及到图像的旋转，仿射，光照等变化，SIFT算法依旧有非常好的匹配效果。

SIFT特征点提取

本文将下面函数为參照顺序介绍SIFT特征点提取与描写叙述方法。

1.图像预处理

2.构建高斯金字塔（不同尺度下的图像）

3.生成DOG尺度空间

4.关键点搜索与定位

5.计算特征点所在的尺度

6.为特征点分配方向角

7.构建特征描写叙述子

/**
   Finds SIFT features in an image using user-specified parameter values.  All
   detected features are stored in the array pointed to by \a feat.
*/
int _sift_features( IplImage* img, struct feature** feat, int intvls,
		    double sigma, double contr_thr, int curv_thr,
		    int img_dbl, int descr_width, int descr_hist_bins )
{
  IplImage* init_img;
  IplImage*** gauss_pyr, *** dog_pyr;
  CvMemStorage* storage;
  CvSeq* features;
  int octvs, i, n = 0;

  /* check arguments */
  if( ! img )
    fatal_error( "NULL pointer error, %s, line %d",  __FILE__, __LINE__ );
  if( ! feat )
    fatal_error( "NULL pointer error, %s, line %d",  __FILE__, __LINE__ );

  /* build scale space pyramid; smallest dimension of top level is ~4 pixels */
  init_img = create_init_img( img, img_dbl, sigma );                            //对进行图片预处理
  octvs = log( MIN( init_img->width, init_img->height ) ) / log(2) - 2;  //计算高斯金字塔的组数(octave),同一时候保证顶层至少有4个像素点
  gauss_pyr = build_gauss_pyr( init_img, octvs, intvls, sigma );  //建立高斯金字塔
  dog_pyr = build_dog_pyr( gauss_pyr, octvs, intvls );   //DOG尺度空间

  storage = cvCreateMemStorage( 0 );
  features = scale_space_extrema( dog_pyr, octvs, intvls, contr_thr,   //极值点检測，并去除不稳定特征点
				  curv_thr, storage );
  calc_feature_scales( features, sigma, intvls );                      //计算特征点所在的尺度
  if( img_dbl )
    adjust_for_img_dbl( features );                                       //假设图像初始被扩大了2倍。全部坐标与尺度要除以2
  calc_feature_oris( features, gauss_pyr );                               //计算特征点所在尺度内的方向角
  compute_descriptors( features, gauss_pyr, descr_width, descr_hist_bins );//计算特征描写叙述子 128维向量

  /* sort features by decreasing scale and move from CvSeq to array */
  cvSeqSort( features, (CvCmpFunc)feature_cmp, NULL );   //对特征点按尺度排序
  n = features->total;
  *feat = calloc( n, sizeof(struct feature) );
  *feat = cvCvtSeqToArray( features, *feat, CV_WHOLE_SEQ );
  for( i = 0; i < n; i++ )
    {
      free( (*feat)[i].feature_data );
      (*feat)[i].feature_data = NULL;
    }

  cvReleaseMemStorage( &storage );
  cvReleaseImage( &init_img );
  release_pyr( &gauss_pyr, octvs, intvls + 3 );
  release_pyr( &dog_pyr, octvs, intvls + 2 );
  return n;
}

—————————————————————————————————————————————————————

1.图像预处理

/************************ Functions prototyped here **************************/

/*
  Converts an image to 8-bit grayscale and Gaussian-smooths it.  The image is
  optionally doubled in size prior to smoothing.

  @param img input image
  @param img_dbl if true, image is doubled in size prior to smoothing
  @param sigma total std of Gaussian smoothing
*/
static IplImage* create_init_img( IplImage* img, int img_dbl, double sigma )
{
  IplImage* gray, * dbl;
  double sig_diff;

  gray = convert_to_gray32( img );   //转换为32位灰度图
  if( img_dbl )                                  // 图像被放大二倍
    {
      sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA * 4 );   //  sigma = 1.6 , SIFT_INIT_SIGMA = 0.5  lowe觉得图像在尺度0.5下最清晰
      dbl = cvCreateImage( cvSize( img->width*2, img->height*2 ),
			   IPL_DEPTH_32F, 1 );
      cvResize( gray, dbl, CV_INTER_CUBIC );  //双三次插值方法 放大图像
      cvSmooth( dbl, dbl, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff );     //高斯平滑
      cvReleaseImage( &gray );
      return dbl;
    }
  else
    {
      sig_diff = sqrt( sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA );
      cvSmooth( gray, gray, CV_GAUSSIAN, 0, 0, sig_diff, sig_diff ); // 高斯平滑
      return gray;
    }
}

lowe建议把初始图像放大二倍。能够得到很多其它的特征点，提取到很多其它细节，而且觉得图像在尺度σ = 0.5时图像最清晰，初始高斯尺度为σ = 1.6。

☆第19行由于图像被放大二倍，此时σ = 1.0 。

由于对二倍化后的图像平滑是在σ = 0.5 上叠加的高斯模糊。

  所以有模糊系数有sig_diff = sqrt (sigma *sigma - 0.5*0.5*4)=sqrt(1.6*1.6 -1) ；

2.构建高斯金字塔

构建高斯金字塔过程即构建出图像在不同尺度上图像，提取到的特征点可有具有尺度不变性。

图像的尺度空间L(x,y,σ)能够用一个高斯函数G(x,y,σ)与图像I(x,y)卷积产生，即L(x,y,σ) = G(x,y,σ) * I(x,y) 

当中二维高斯核的计算为             。

☆不同的尺度空间即用不同的高斯核函数平滑图像， 平滑系数越大。图像越模糊。即模拟出动物的视觉效果，由于事先不知道物体的大小，在不同的尺度下，图像的细节会表现的不同。当尺度由小变大的过程中，是一个细节逐步简化的过程，图像中特征不够明显的物体，就模糊的多了。而有些物体还能够看得到大致的轮廓。所以要在不同尺度下。观察物体的尺度响应，提取到的特征才干具有尺度不变性。

SIFT算法採用高斯金字塔实现连续的尺度空间的图像。金字塔共分为O(octave)组。每组有S(intervals)层 ，下一组是由上一组隔点採样得到（即降2倍分辨率），这是为了减轻卷积运算的工作量。

构建高斯金字塔（octave = 5, intervals +3=6）：

所有空间尺度为： 

                                         

☆1.这个尺度因子都是在原图上进行的。而在算法实现过程中，採用高斯平滑是在上一层图像上再叠加高斯平滑。即我们在程序中看到的平滑因子为

            

Eg. 在第一层上为了得到kσ的高斯模糊图像，能够在原图上直接採用kσ平滑，也能够在上一层图像上（已被σ平滑）的图像上採用平滑因子为平滑图像，效果是一样的。

 ☆2.我们在源代码上同一时候也没有看到组间的2倍的关系，实际在对每组的平滑因子都是一样的，2倍的关系是因为在降採样的过程中产生的，第二层的第一张图是由第一层的平滑因子为2σ的图像上（即倒数第三张）降採样得到，此时图像平滑因子为σ，所以继续採用以上的平滑因子。

但在原图上看。形成了所有的空间尺度。

☆3.每组（octave）有S+3层图像，是因为在DOG尺度空间上寻找极值点的方法是在一个立方体内进行，即上下层比較。所以不在DOG空间的第一层与最后一层寻找，即DOG须要S+2层图像，因为DOG尺度空间是由高斯金字塔相邻图像相减得到，即每组须要S+3层图像。

/*
  Builds Gaussian scale space pyramid from an image
  @param base base image of the pyramid
  @param octvs number of octaves of scale space
  @param intvls number of intervals per octave
  @param sigma amount of Gaussian smoothing per octave

  @return Returns a Gaussian scale space pyramid as an octvs x (intvls + 3)
    array 

给定组数(octave)和层数(intvls)。以及初始平滑系数sigma,构建高斯金字塔
返回的每组中层数为intvls+3
*/
static IplImage*** build_gauss_pyr( IplImage* base, int octvs,
			     int intvls, double sigma )
{
  IplImage*** gauss_pyr;
  const int _intvls = intvls;             // lowe 採用了每组层数(intvls)为 3
 // double  sig_total, sig_prev;
	 double  k;
  int i, o;
  double *sig = (double *)malloc(sizeof(int)*(_intvls+3));  //存储每组的高斯平滑因子，每组相应的平滑因子都同样

  gauss_pyr = calloc( octvs, sizeof( IplImage** ) );
  for( i = 0; i < octvs; i++ )
    gauss_pyr[i] = calloc( intvls + 3, sizeof( IplImage *) );

  /*
    precompute Gaussian sigmas using the following formula:

    \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2

    sig[i] is the incremental sigma value needed to compute
    the actual sigma of level i. Keeping track of incremental
    sigmas vs. total sigmas keeps the gaussian kernel small.
  */
  k = pow( 2.0, 1.0 / intvls );                 // k = 2^(1/S)
  sig[0] = sigma;
  sig[1] = sigma * sqrt( k*k- 1 );
  for (i = 2; i < intvls + 3; i++)
      sig[i] = sig[i-1] * k;                       //每组相应的平滑因子为 σ ,  sqrt(k^2 -1)* σ, sqrt(k^2 -1)* kσ , ...

  for( o = 0; o < octvs; o++ )
    for( i = 0; i < intvls + 3; i++ )
      {
	if( o == 0  &&  i == 0 )
	  gauss_pyr[o][i] = cvCloneImage(base);                       //第一组。第一层为原图

	/* base of new octvave is halved image from end of previous octave */
	else if( i == 0 )
	  gauss_pyr[o][i] = downsample( gauss_pyr[o-1][intvls] );  //第一层图像由上一层倒数第三张隔点採样得到

	/* blur the current octave's last image to create the next one */
	else
	  {
	    gauss_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i-1]),
					     IPL_DEPTH_32F, 1 );
	    cvSmooth( gauss_pyr[o][i-1], gauss_pyr[o][i],
		      CV_GAUSSIAN, 0, 0, sig[i], sig[i] );                       //高斯平滑
	  }
      }

  return gauss_pyr;
}

3.生成DOG尺度空间

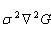Lindeberg发现高斯差分函数（Difference of Gaussian 。简称DOG算子）与尺度归一化的高斯拉普拉斯函数很近似，且

 

差分近似：

lowe建议採用相邻尺度的图像相减来获得高斯差分图像D(x,y,σ)来近似LOG来进行极值检測。

D(x,y,σ) = G(x,y,kσ)*I(x,y)-G(x,y,σ)*I(x,y)

              =L(x,y,kσ) - L(x,y,σ)

对高斯金字塔的每组内相邻图像相减。形成DOG尺度空间，这时DOG中每组有S+2层图像

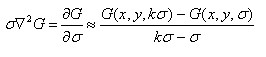
static IplImage*** build_dog_pyr( IplImage*** gauss_pyr, int octvs, int intvls )
{
  IplImage*** dog_pyr;
  int i, o;

  dog_pyr = calloc( octvs, sizeof( IplImage** ) );
  for( i = 0; i < octvs; i++ )
    dog_pyr[i] = calloc( intvls + 2, sizeof(IplImage*) );

  for( o = 0; o < octvs; o++ )
    for( i = 0; i < intvls + 2; i++ )
      {
	dog_pyr[o][i] = cvCreateImage( cvGetSize(gauss_pyr[o][i]),
				       IPL_DEPTH_32F, 1 );
	cvSub( gauss_pyr[o][i+1], gauss_pyr[o][i], dog_pyr[o][i], NULL );   //相邻两层图像相减，结果放在dog_pyr数组内
      }

  return dog_pyr;
}

4.关键点搜索与定位

  在DOG尺度空间上，首先寻找极值点，插值处理，找到准确的极值点坐标，再排除不稳定的特征点（边界点）

/*
  Detects features at extrema in DoG scale space.  Bad features are discarded
  based on contrast and ratio of principal curvatures.

  @return Returns an array of detected features whose scales, orientations,
    and descriptors are yet to be determined.
*/
static CvSeq* scale_space_extrema( IplImage*** dog_pyr, int octvs, int intvls,
				   double contr_thr, int curv_thr,
				   CvMemStorage* storage )
{
  CvSeq* features;
  double prelim_contr_thr = 0.5 * contr_thr / intvls; //极值比較前的阈值处理
  struct feature* feat;
  struct detection_data* ddata;
  int o, i, r, c;

  features = cvCreateSeq( 0, sizeof(CvSeq), sizeof(struct feature), storage );
  for( o = 0; o < octvs; o++ )                     //对DOG尺度空间上，遍历从第二层图像開始到倒数第二层图像上。每一个像素点
    for( i = 1; i <= intvls; i++ )
      for(r = SIFT_IMG_BORDER; r < dog_pyr[o][0]->height-SIFT_IMG_BORDER; r++)
	for(c = SIFT_IMG_BORDER; c < dog_pyr[o][0]->width-SIFT_IMG_BORDER; c++)
	  /* perform preliminary check on contrast */
	  if( ABS( pixval32f( dog_pyr[o][i], r, c ) ) > prelim_contr_thr )    // 排除像素值小于阈值prelim_contr_thr的点，提高稳定性
	    if( is_extremum( dog_pyr, o, i, r, c ) )             //与周围26个像素值比較，是否极大值或者极小值点
	      {
		feat = interp_extremum(dog_pyr, o, i, r, c, intvls, contr_thr); //插值处理，找到准确的特征点坐标
		if( feat )
		  {
		    ddata = feat_detection_data( feat );
		    if( ! is_too_edge_like( dog_pyr[ddata->octv][ddata->intvl],   //依据Hessian矩阵 推断是否为边缘上的点
					    ddata->r, ddata->c, curv_thr ) )
		      {
			cvSeqPush( features, feat );          //是特征点进入特征点序列
		      }
		    else
		      free( ddata );
		    free( feat );
		  }
	      }

  return features;
}

4.1

寻找极值点

在DOG尺度空间上。每组有S+2层图像。每一组都从第二层開始每个像素点都要与它相邻的像素点比較，看是否比它在图像域或尺度域的全部点的值大或者小。

与它同尺度的相邻像素点有8个，上下相邻尺度的点共同拥有2×9=18。共同拥有26个像素点。也就在一个3×3的立方体内进行。搜索的过程是第二层開始到倒数第二层结束，共检測了octave组。每组S层。

  

/*
  Determines whether a pixel is a scale-space extremum by comparing it to it's
  3x3x3 pixel neighborhood.
*/
static int is_extremum( IplImage*** dog_pyr, int octv, int intvl, int r, int c )
{
  double val = pixval32f( dog_pyr[octv][intvl], r, c );
  int i, j, k;

  /* check for maximum */
  if( val > 0 )
    {
      for( i = -1; i <= 1; i++ )
	for( j = -1; j <= 1; j++ )
	  for( k = -1; k <= 1; k++ )
	    if( val < pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
	      return 0;
    }

  /* check for minimum */
  else
    {
      for( i = -1; i <= 1; i++ )
	for( j = -1; j <= 1; j++ )
	  for( k = -1; k <= 1; k++ )
	    if( val > pixval32f( dog_pyr[octv][intvl+i], r + j, c + k ) )
	      return 0;
    }

  return 1;
}

4.2

准确定位特征点

      以上的极值点搜索是在离散空间进行的，极值点不真正意义上的极值点。通过对空间尺度函数拟合。能够得到亚像素级像素点坐标。

尺度空间的Taylor展开式：

                                      ，当中

求导并令其为0，得到亚像素级：

                                           

相应的函数值为：

                                        

 

是一个三维矢量，矢量在不论什么一个方向上的偏移量大于0.5时，意味着已经偏离了原像素点，这种特征坐标位置须要更新或者继续插值计算。算法实现过程中，为了保证插值可以收敛，设置了最大插值次数（lowe 设置了5次）。

同一时候当时（本文阈值採用了0.04/S）
，特征点才被保留，由于响应值过小的点。easy受噪声的干扰而不稳定。

对离散空间进行函数拟合（插值）：

/*
  Performs one step of extremum interpolation.  Based on Eqn. (3) in Lowe's
  paper.

  r,c 为特征点位置，xi,xr,xc,保存三个方向的偏移量
*/

static void interp_step( IplImage*** dog_pyr, int octv, int intvl, int r, int c,
			 double* xi, double* xr, double* xc )
{
  CvMat* dD, * H, * H_inv, X;
  double x[3] = { 0 };

  dD = deriv_3D( dog_pyr, octv, intvl, r, c );      //计算三个方向的梯度
  H = hessian_3D( dog_pyr, octv, intvl, r, c );    // 计算3维空间的hessian矩阵
  H_inv = cvCreateMat( 3, 3, CV_64FC1 );
  cvInvert( H, H_inv, CV_SVD );           //计算逆矩阵
  cvInitMatHeader( &X, 3, 1, CV_64FC1, x, CV_AUTOSTEP );
  cvGEMM( H_inv, dD, -1, NULL, 0, &X, 0 );   //广义乘法 

  cvReleaseMat( &dD );
  cvReleaseMat( &H );
  cvReleaseMat( &H_inv );

  *xi = x[2];
  *xr = x[1];
  *xc = x[0];
}

/*
  Interpolates a scale-space extremum's location and scale to subpixel
  accuracy to form an image feature.
*/
static struct feature* interp_extremum( IplImage*** dog_pyr, int octv,          //通过拟合求取准确的特征点位置
					int intvl, int r, int c, int intvls,
					double contr_thr )
{
  struct feature* feat;
  struct detection_data* ddata;
  double xi, xr, xc, contr;
  int i = 0;

  while( i < SIFT_MAX_INTERP_STEPS )   //在最大迭代次数范围内进行
    {
      interp_step( dog_pyr, octv, intvl, r, c, &xi, &xr, &xc );          //插值后得到的三个方向的偏移量(xi,xr,xc)
      if( ABS( xi ) < 0.5  &&  ABS( xr ) < 0.5  &&  ABS( xc ) < 0.5 )
	break;

      c += cvRound( xc );    //更新位置
      r += cvRound( xr );
      intvl += cvRound( xi );

      if( intvl < 1  ||
	  intvl > intvls  ||
	  c < SIFT_IMG_BORDER  ||
	  r < SIFT_IMG_BORDER  ||
	  c >= dog_pyr[octv][0]->width - SIFT_IMG_BORDER  ||
	  r >= dog_pyr[octv][0]->height - SIFT_IMG_BORDER )
	{
	  return NULL;
	}

      i++;
    }

  /* ensure convergence of interpolation */
  if( i >= SIFT_MAX_INTERP_STEPS )
    return NULL;

  contr = interp_contr( dog_pyr, octv, intvl, r, c, xi, xr, xc );     //计算插值后相应的函数值
  if( ABS( contr ) < contr_thr / intvls )   //小于阈值（0.04/S）的点。则丢弃
    return NULL;

  feat = new_feature();
  ddata = feat_detection_data( feat );
  feat->img_pt.x = feat->x = ( c + xc ) * pow( 2.0, octv );       // 计算特征点依据降採样的次数相应于原图中位置
  feat->img_pt.y = feat->y = ( r + xr ) * pow( 2.0, octv );
  ddata->r = r;                  // 在本尺度内的坐标位置
  ddata->c = c;
  ddata->octv = octv;                 //组信息
  ddata->intvl = intvl;                 // 层信息
  ddata->subintvl = xi;              // 层方向的偏移量

  return feat;
}

4.3

删除边缘效应

为了得到稳定的特征点。要删除掉落在图像边缘上的点。

一个落在边缘上的点。能够依据主曲率计算推断。主曲率能够通过2维的 Hessian矩阵求出；

在边缘上的点，必然使得Hessian矩阵的两个特征值相差比較大。而特征值与矩阵元素有下面关系；

令α=rβ ，所以有：

我们能够推断上述公式的比值大小，大于阈值（lowe採用 r =10）的点排除。

static int is_too_edge_like( IplImage* dog_img, int r, int c, int curv_thr )
{
  double d, dxx, dyy, dxy, tr, det;

  /* principal curvatures are computed using the trace and det of Hessian */
  d = pixval32f(dog_img, r, c);                                                                             //计算Hessian 矩阵内的4个元素值
  dxx = pixval32f( dog_img, r, c+1 ) + pixval32f( dog_img, r, c-1 ) - 2 * d;
  dyy = pixval32f( dog_img, r+1, c ) + pixval32f( dog_img, r-1, c ) - 2 * d;
  dxy = ( pixval32f(dog_img, r+1, c+1) - pixval32f(dog_img, r+1, c-1) -
	  pixval32f(dog_img, r-1, c+1) + pixval32f(dog_img, r-1, c-1) ) / 4.0;
  tr = dxx + dyy;                          //矩阵的迹
  det = dxx * dyy - dxy * dxy;     //矩阵的值

  /* negative determinant -> curvatures have different signs; reject feature */
  if( det <= 0 )     // 矩阵值为负值。说明曲率有不同符号，丢弃
    return 1;

  if( tr * tr / det < ( curv_thr + 1.0 )*( curv_thr + 1.0 ) / curv_thr )   //比值小于阈值的特征点被保留  curv_thr = 10
    return 0;
  return 1;
}

5.计算特征点相应的尺度

static void calc_feature_scales( CvSeq* features, double sigma, int intvls )
{
  struct feature* feat;
  struct detection_data* ddata;
  double intvl;
  int i, n;

  n = features->total;
  for( i = 0; i < n; i++ )
    {
      feat = CV_GET_SEQ_ELEM( struct feature, features, i );
      ddata = feat_detection_data( feat );
      intvl = ddata->intvl + ddata->subintvl;
      feat->scl = sigma * pow( 2.0, ddata->octv + intvl / intvls );      // feat->scl 保存特征点在整体上尺度
      ddata->scl_octv = sigma * pow( 2.0, intvl / intvls );     // feat->feature_data->scl__octv 保存特征点在组内的尺度，用来以下计算方向角
    }
}

6.为特征点分配方向角

这部分包含：计算邻域内梯度直方图，平滑直方图，复制特征点（有辅方向的特征点）

static void calc_feature_oris( CvSeq* features, IplImage*** gauss_pyr )
{
  struct feature* feat;
  struct detection_data* ddata;
  double* hist;
  double omax;
  int i, j, n = features->total;

  for( i = 0; i < n; i++ )
    {
      feat = malloc( sizeof( struct feature ) );
      cvSeqPopFront( features, feat );
      ddata = feat_detection_data( feat );
      hist = ori_hist( gauss_pyr[ddata->octv][ddata->intvl],     // 计算邻域内的梯度直方图,邻域半径radius = 3*1.5*sigma;  高斯加权系数= 1.5 *sigma
		       ddata->r, ddata->c, SIFT_ORI_HIST_BINS,
		       cvRound( SIFT_ORI_RADIUS * ddata->scl_octv ),
		       SIFT_ORI_SIG_FCTR * ddata->scl_octv );
      for( j = 0; j < SIFT_ORI_SMOOTH_PASSES; j++ )
	smooth_ori_hist( hist, SIFT_ORI_HIST_BINS );    // 对直方图平滑
      omax = dominant_ori( hist, SIFT_ORI_HIST_BINS ); // 返回直方图的主方向
      add_good_ori_features( features, hist, SIFT_ORI_HIST_BINS,//大于主方向的80%为辅方向
			     omax * SIFT_ORI_PEAK_RATIO, feat );
      free( ddata );
      free( feat );
      free( hist );
    }
}

6.1

建立特征点邻域内的直方图

上一步scl_octv保存了每一个特征点所在的组内尺度。以下计算特征点所在尺度内的高斯图像，以3×1.5×scl_octv为半径的区域内的全部像素点的梯度幅值与幅角；

计算公式：

在计算全然部特征点的幅值与幅角后。使用直方图统计。直方图横轴为梯度方向角，纵轴为相应幅值的累加值（与权重），梯度方向范围为0~360度，划分为36个bin,每一个bin的宽度为10。

下图描写叙述的划分为8个bin,每一个bin的宽度为45的效果图：

其次。每一个被增加直方图的幅值，要进行权重处理，权重也是採用高斯加权函数。当中高斯系数为1.5×scl_octv。通过高斯加权使特征点附近的点有较大的权重，能够弥补部分因没有仿射不变性而产生的不稳定问题；

即每一个bin值按以下的公式累加，mag是幅值，后面为权重；i，j,为偏离特征点距离：

☆程序上能够帮助你理解上面的概念：

static double* ori_hist( IplImage* img, int r, int c, int n, int rad,
			 double sigma )
{
  double* hist;
  double mag, ori, w, exp_denom, PI2 = CV_PI * 2.0;
  int bin, i, j;

  hist = calloc( n, sizeof( double ) );
  exp_denom = 2.0 * sigma * sigma;
  for( i = -rad; i <= rad; i++ )
    for( j = -rad; j <= rad; j++ )
      if( calc_grad_mag_ori( img, r + i, c + j, &mag, &ori ) )    //计算领域像素点的梯度幅值mag与方向ori
	{
	  w = exp( -( i*i + j*j ) / exp_denom );                    //高斯权重
	  bin = cvRound( n * ( ori + CV_PI ) / PI2 );
	  bin = ( bin < n )?

bin : 0;
	  hist[bin] += w * mag;                             //直方图上累加
	}

  return hist;  //返回累加完毕的直方图
}

6.2

平滑直方图

lowe建议对直方图进行平滑，降低突变的影响。

static void smooth_ori_hist( double* hist, int n )
{
  double prev, tmp, h0 = hist[0];
  int i;

  prev = hist[n-1];
  for( i = 0; i < n; i++ )
    {
      tmp = hist[i];
      hist[i] = 0.25 * prev + 0.5 * hist[i] +
	0.25 * ( ( i+1 == n )? h0 : hist[i+1] );
      prev = tmp;
    }
}

6.3

复制特征点

在上面的直方图上，我们已经找到了特征点主方向的峰值omax,当存在还有一个大于主峰值80%的峰值时，将这个方向作为特征点的辅方向，即一个特征点有多个方向，这能够增强匹配的鲁棒性。在算法上，即把该特征点复制多份作为新的特征点。新特征点的方向为这些辅方向，其它属性保持一致。

static void add_good_ori_features( CvSeq* features, double* hist, int n,
				   double mag_thr, struct feature* feat )
{
  struct feature* new_feat;
  double bin, PI2 = CV_PI * 2.0;
  int l, r, i;

  for( i = 0; i < n; i++ )                   //检查全部的方向
    {
      l = ( i == 0 )?

n - 1 : i-1;
      r = ( i + 1 ) % n;

      if( hist[i] > hist[l]  &&  hist[i] > hist[r]  &&  hist[i] >= mag_thr ) //推断是不是幅方向
	{
	  bin = i + interp_hist_peak( hist[l], hist[i], hist[r] );     //插值离散处理。取得更精确的方向
	  bin = ( bin < 0 )? n + bin : ( bin >= n )?

bin - n : bin;
	  new_feat = clone_feature( feat );       //复制特征点
	  new_feat->ori = ( ( PI2 * bin ) / n ) - CV_PI;//  为特征点方向赋值[-180,180]
	  cvSeqPush( features, new_feat );  //
	  free( new_feat );
	}
    }
}

7.构建特征描写叙述子

眼下每一个特征点具有属性有位置、方向、尺度三个信息，如今要用一个向量去描写叙述这个特征点，使其具有高度的唯一特征性。

1.lowe採用了把特征点邻域划分成 d×d (lowe建议d=4) 个子区域，然后再统计每一个子区域的方向直方图（8个方向），直方图横轴有8个bin,纵轴为梯度幅值（×权重）的累加。这样描写叙述这个特征点的向量为4×4×8=128维。每一个子区域的宽度建议为3×octv，octv为组内的尺度。考虑到插值问题。特征点的邻域范围边长为3×octv×(d+1)。考虑到旋转问题,邻域的范围边长为3×octv×(d+1)×sqrt(2)。最后半径为：

2.把坐标系旋转到主方向位置。再次统计邻域内全部像素点的梯度幅值与方向，计算所在子区域。并把幅值×权重累加到这个子区域的直方图上。

算法上即统计每一个邻域的方向直方图时。所有是相对于这个特征点的主方向的方向。

假设主方向为30度,某个像素点的梯度方向为50度。这时统计到该子区域直方图上就成了20度。同一时候因为旋转，这时权重也必须是按旋转后的坐标。

计算所在的子区域的位置：

  

权重按高斯加权函数。系数为描写叙述子宽度的一半，即0.5d：

static double*** descr_hist( IplImage* img, int r, int c, double ori,
			     double scl, int d, int n )
{
  double*** hist;
  double cos_t, sin_t, hist_width, exp_denom, r_rot, c_rot, grad_mag,
    grad_ori, w, rbin, cbin, obin, bins_per_rad, PI2 = 2.0 * CV_PI;
  int radius, i, j;

  hist = calloc( d, sizeof( double** ) );
  for( i = 0; i < d; i++ )
    {
      hist[i] = calloc( d, sizeof( double* ) );
      for( j = 0; j < d; j++ )
	hist[i][j] = calloc( n, sizeof( double ) );
    }

  cos_t = cos( ori );
  sin_t = sin( ori );
  bins_per_rad = n / PI2;
  exp_denom = d * d * 0.5;
  hist_width = SIFT_DESCR_SCL_FCTR * scl;
  radius = hist_width * sqrt(2) * ( d + 1.0 ) * 0.5 + 0.5;   //计算邻域范围半径，+0.5为了取得很多其它元素
  for( i = -radius; i <= radius; i++ )
    for( j = -radius; j <= radius; j++ )
      {
	/*
	  Calculate sample's histogram array coords rotated relative to ori.
	  Subtract 0.5 so samples that fall e.g. in the center of row 1 (i.e.
	  r_rot = 1.5) have full weight placed in row 1 after interpolation.
	*/
	c_rot = ( j * cos_t - i * sin_t ) / hist_width;              //
	r_rot = ( j * sin_t + i * cos_t ) / hist_width;
	rbin = r_rot + d / 2 - 0.5;                                        //旋转后相应的x``及y''
	cbin = c_rot + d / 2 - 0.5;

	if( rbin > -1.0  &&  rbin < d  &&  cbin > -1.0  &&  cbin < d )
	  if( calc_grad_mag_ori( img, r + i, c + j, &grad_mag, &grad_ori ))       //计算每一个像素点的梯度方向、幅值、
	    {
	      grad_ori -= ori;              //每一个像素点相对于特征点的梯度方向
	      while( grad_ori < 0.0 )
		grad_ori += PI2;
	      while( grad_ori >= PI2 )
		grad_ori -= PI2;

	      obin = grad_ori * bins_per_rad;     //像素梯度方向转换成8个方向
	      w = exp( -(c_rot * c_rot + r_rot * r_rot) / exp_denom );     //每一个子区域内像素点，相应的权重
	      interp_hist_entry( hist, rbin, cbin, obin, grad_mag * w, d, n );   //为了减小突变影响对附近三个bin值三线性插值处理
	    }
      }

  return hist;
}

每一个维度上bin值累加方法，即计算一个像素的幅值对于相邻的方向，以及位置的贡献，dr，dc为相邻位置，do为相邻方向

，这就是128维向量的数据，计算方法

static void interp_hist_entry( double*** hist, double rbin, double cbin,
			       double obin, double mag, int d, int n )
{
  double d_r, d_c, d_o, v_r, v_c, v_o;
  double** row, * h;
  int r0, c0, o0, rb, cb, ob, r, c, o;

  r0 = cvFloor( rbin );
  c0 = cvFloor( cbin );
  o0 = cvFloor( obin );
  d_r = rbin - r0;
  d_c = cbin - c0;
  d_o = obin - o0;

  /*
    The entry is distributed into up to 8 bins.  Each entry into a bin
    is multiplied by a weight of 1 - d for each dimension, where d is the
    distance from the center value of the bin measured in bin units.
  */
  for( r = 0; r <= 1; r++ )
    {
      rb = r0 + r;
      if( rb >= 0  &&  rb < d )
	{
	  v_r = mag * ( ( r == 0 )? 1.0 - d_r : d_r );
	  row = hist[rb];
	  for( c = 0; c <= 1; c++ )
	    {
	      cb = c0 + c;
	      if( cb >= 0  &&  cb < d )
		{
		  v_c = v_r * ( ( c == 0 )? 1.0 - d_c : d_c );
		  h = row[cb];
		  for( o = 0; o <= 1; o++ )
		    {
		      ob = ( o0 + o ) % n;
		      v_o = v_c * ( ( o == 0 )? 1.0 - d_o : d_o );
		      h[ob] += v_o;
		    }
		}
	    }
	}
    }
}

最后为了去除光照的影响。对128维向量进行归一化处理。同一时候设置门限，大于0.2的梯度幅值截断

static void hist_to_descr( double*** hist, int d, int n, struct feature* feat )
{
  int int_val, i, r, c, o, k = 0;

  for( r = 0; r < d; r++ )
    for( c = 0; c < d; c++ )
      for( o = 0; o < n; o++ )
	feat->descr[k++] = hist[r][c][o];

  feat->d = k;
  normalize_descr( feat );          //向量归一化
  for( i = 0; i < k; i++ )
    if( feat->descr[i] > SIFT_DESCR_MAG_THR )   //设置门限，门限为0.2
      feat->descr[i] = SIFT_DESCR_MAG_THR;
  normalize_descr( feat );      //向量归一化

  /* convert floating-point descriptor to integer valued descriptor */
  for( i = 0; i < k; i++ )              //换成整形值
    {
      int_val = SIFT_INT_DESCR_FCTR * feat->descr[i];
      feat->descr[i] = MIN( 255, int_val );
    }
}

最后对特征点按尺度大小进行排序，强特征点放在前面；

这样每一个特征点就相应一个128维的向量，接下来能够用能够用向量做以后的匹配工作了。

特征点匹配原理后序文章会更新~

------------------------------------------------------------------------------------

在此很感谢CSDN上几位图像上的大牛，我也是通过他们的文章去学习研究的，本文也是參考了他们的文章才写成！

推荐看大牛们的文章。原理写的非常好！

http://blog.csdn.net/abcjennifer/article/details/7639681

http://blog.csdn.net/zddblog/article/details/7521424

http://blog.csdn.net/chen825919148/article/details/7685952

http://blog.csdn.net/xiaowei_cqu/article/details/8069548