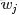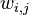主题模型LDA及在推荐系统中的应用
1 关于主题模型
使用LDA做推荐已经有一段时间了,LDA的推导过程反复看过很多遍,今天有点理顺的感觉,就先写一版。
- 隐含狄利克雷分布简称LDA(latent dirichlet allocation),是主题模型(topic model)的一种,由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出。 主题模型属于聚类方法,是一种无监督的学习方法。
- 与通常的tf-idf相比,主题模型重在可以在语义上计算文本内容的相关性。主题模型是一种词袋模型,即只考虑文本总的词频,不考虑顺序。
- 假设依据是一篇文本以一定的概率属于多个主题(概率相加为1),一个词也以一定的概率属于多个主题(一个词可能以不同的概率属于不同的主题)。
- 参数的先验
topic-word分布受一个参数为α的对称Dirichlet约束
doc-topic分布受一个参数为β的对称Dirichlet约束
2 频率学派与贝叶斯学派
这里简单介绍频率学派和贝叶斯学派,因为PLSA和LDA分别用的是这两种学派的思想。
- 直至今日,关于统计推断的主张和想法,大体可以纳入到两个体系之内,其一叫频率学派,其特征是把需要推断的参数θ视作固定且未知的常数,而样本X是随机的,其着眼点在样本空间,有关的概率计算都是针对X的分布。另一派叫做贝叶斯学派,他们把参数θ视作随机变量,而样本X是固定的,其着眼点在参数空间,重视参数θ的分布,固定的操作模式是通过参数的先验分布结合样本信息得到参数的后验分布。
以抛硬币为例,正面朝上的概率是待求的参数。
- 往小处说,频率派认为参数是客观存在,不会改变,虽然未知,但却是固定值;贝叶斯派则认为参数是随机值,因为没有观察到,那么和是一个随机数也没有什么区别,因此参数也可以有分布。
- 往大处说,频率派最常关心的是似然函数,而贝叶斯派最常关心的是后验分布。我们会发现,后验分布其实就是似然函数乘以先验分布再normalize一下使其积分到1。因此两者的很多方法都是相通的。贝叶斯派因为所有的参数都是随机变量,都有分布,因此可以使用一些基于采样的方法(如MCMC)使得我们更容易构建复杂模型。频率派的优点则是没有假设一个先验分布,因此更加客观,也更加无偏。
- 例如,概率学派可能任务抛硬币证明朝上的概率就是0.5;而贝叶斯学派先取得一个先验概率,在通过做试验观察,结合先验概率和观察结果得出一个后验概率,这个后验概率才是硬币证明朝上的概率,后验概率本身也符合某种分布。
- LDA是三层贝叶斯模型。 简单的说,一篇文章可以以不同的概率属于多个主题,但分别以多大的概率属于这些主题呢?例如文章A可以是{‘科技’:0.5, ‘体育’:0.2, ‘财经’:0.3}这种分布, 也可能是{‘科技’:0.4, ‘体育’:0.4, ‘财经’:0.2}这种分布. 贝叶斯学派认为这个分布也服从一定分布,这里用的就是狄利克雷分布,即它在LDA中其实是一个分布的分布。并且,LDA用到两次Dilichlet:一个主题中词的概率分布也服从狄利克雷分布。
3 PLSA与LDA
介绍PLSA和LDA两种生产模型。
3.1 PLSA
3.1.1 举个生成文本的例子
一篇文章往往有多个主题,只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中,往往会分别从教育、经济、交通等多个主题进行介绍。那么在pLSA中,文档是怎样被生成的呢?
假设你要写M篇文档,由于一篇文档由各个不同的词组成,所以你需要确定每篇文档里每个位置上的词。
再假定你一共有K个可选的主题,有V个可选的词,咱们来玩一个扔骰子的游戏。
- 假设你每写一篇文档会制作一颗K面的“文档-主题”骰子(扔此骰子能得到K个主题中的任意一个),和K个V面的“主题-词项” 骰子(每个骰子对应一个主题,K个骰子对应之前的K个主题,且骰子的每一面对应要选择的词项,V个面对应着V个可选的词)。
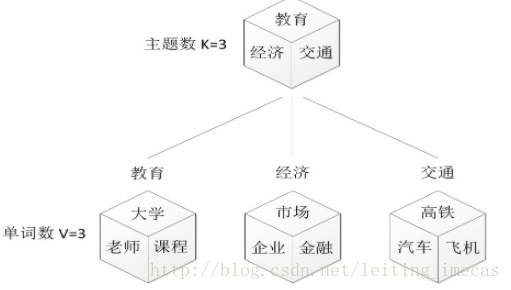
比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。 - 每写一个词,先扔该“文档-主题”骰子选择主题,得到主题的结果后,使用和主题结果对应的那颗“主题-词项”骰子,扔该骰子选择要写的词。
先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
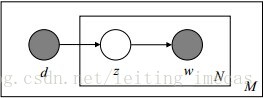
上面这个投骰子产生词的过程简化下便是:“先以一定的概率选取主题,再以一定的概率选取词”。事实上,一开始可供选择的主题有3个:教育、经济、交通,那为何偏偏选取教育这个主题呢?其实是随机选取的,只是这个随机遵循一定的概率分布。比如可能选取教育主题的概率是0.5,选取经济主题的概率是0.3,选取交通主题的概率是0.2,那么这3个主题的概率分布便是{教育:0.5,经济:0.3,交通:0.2},我们把各个主题z在文档d中出现的概率分布称之为主题分布,且是一个多项分布。
同样的,从主题分布中随机抽取出教育主题后,依然面对着3个词:大学、老师、课程,这3个词都可能被选中,但它们被选中的概率也是不一样的。比如大学这个词被选中的概率是0.5,老师这个词被选中的概率是0.3,课程被选中的概率是0.2,那么这3个词的概率分布便是{大学:0.5,老师:0.3,课程:0.2},我们把各个词语w在主题z下出现的概率分布称之为词分布,这个词分布也是一个多项分布。
所以,选主题和选词都是两个随机的过程,先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。 - 最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M次,则完成M篇文档。
3.1.2 流程总结
pLSA中生成文档的整个过程便是选定文档生成主题,确定主题生成词:
- 按照概率
选择一篇文档
- 选定文档
后,从主题分布中按照概率
选择一个隐含的主题类别
选定后,从词分布中按照概率
选择一个词
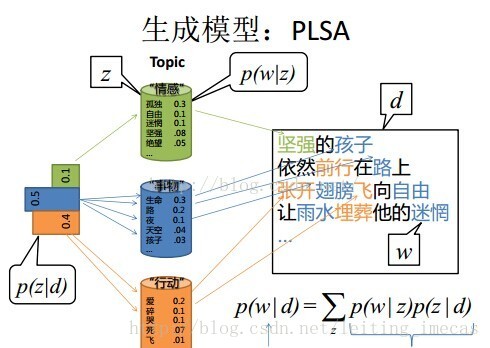
如下图所示(图中被涂色的d、w表示可观测变量,未被涂色的z表示未知的隐变量,N表示一篇文档中总共N个单词,M表示M篇文档):
上图中,文档d和词w是我们得到的样本(样本随机,参数虽未知但固定,所以pLSA属于频率派思想。区别于下文要介绍的LDA中:样本固定,参数未知但不固定,是个随机变量,服从一定的分布,所以LDA属于贝叶斯派思想),可观测得到,所以对于任意一篇文档,其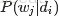
从而可以根据大量已知的文档-词项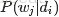
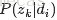
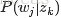
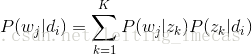
故得到文档中每个词的生成概率为: 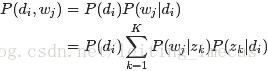
由于可事先计算求出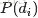
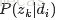
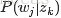
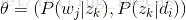
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。 本文不展开介绍。
3.2 LDA
LDA就是在pLSA的基础上加层贝叶斯框架。pLSA样本随机,参数虽未知但固定,属于频率派思想;而LDA样本固定,参数未知但不固定,是个随机变量,服从一定的分布,LDA属于贝叶斯派思想。 这里的参数是指文档的主题分布、主题的词分布。
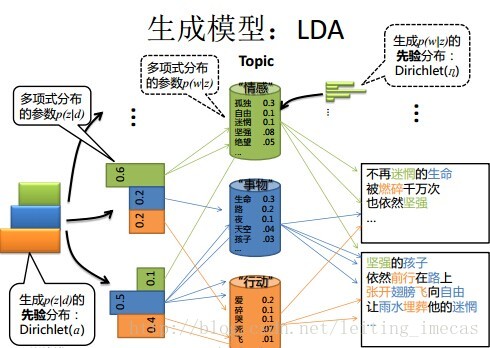
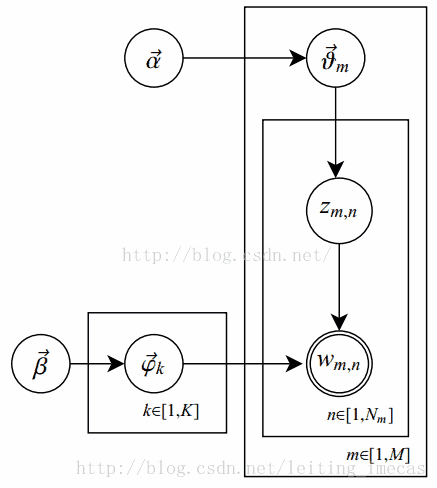
3.2.1 LDA流程
从上图可以看出,lda中,依据Dirichlet采样到了不同的文档-主题分布和主题-词分布。
- 1
- 2
- Boxed:
K is the number of topics
N is the number of words in the document
M is the number of documents to analyse - α is the Dirichlet-prior concentration parameter of the per-document topic distribution
- β is the same parameter of the per-topic word distribution
- φ(k) is the word distribution for topic k
- θ(i) is the topic distribution for document i
- z(i,j) is the topic assignment for w(i,j)
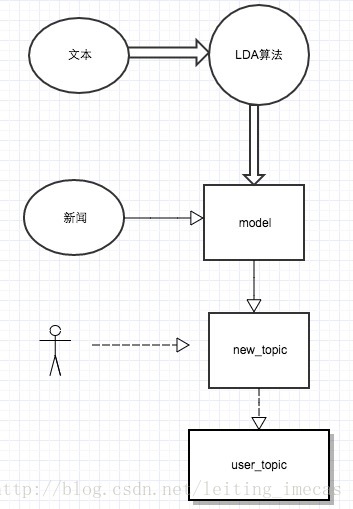
- w(i,j) is the j-th word in the i-th document
- φ and θ are Dirichlet distributions, z and w are multinomials.
生成文本的过程:
LDA模型中一篇文档生成的方式:
- 按照先验概率
选择一篇文档
- 从狄利克雷分布α中取样生成文档
的主题分布
,换言之,主题分布
由超参数为α的Dirichlet分布生成
- 从主题的多项式分布
中取样生成文档
第 j 个词的主题
- 从狄利克雷分布(即Dirichlet分布)β中取样生成主题
对应的词语分布,换言之,词语分布
由参数为β的Dirichlet分布生成
- 从词语的多项式分布
中采样最终生成词语
3.2.2 Gibbs LDA
前面已经介绍了LDA流程,最终的目标函数是个联合概率。待求的doc-topic和topic-word两个矩阵,是借助上述流程中的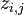
4 在推荐算法中的应用
步骤:
1. 离线求的模型
2. 用模型对新文本预测topic,取topic概率带到阈值(例如0.2)且topN个topic,例如doc1 :topic1:0.5, topic2:0.2
3. 用户点击doc1,就说明用户对topic1和topic2感兴趣,保存用户新闻分析结果,以待推荐
主题模型LDA及在推荐系统中的应用的更多相关文章
- 主题模型TopicModel:主题模型LDA的应用
http://blog.csdn.net/pipisorry/article/details/45665779 主题模型LDA的应用 拿到这些topic后继续后面的这些应用怎么做呢:除了推断出这些主题 ...
- 主题模型 LDA 入门
主题模型 LDA 入门(附 Python 代码) 一.主题模型 在文本挖掘领域,大量的数据都是非结构化的,很难从信息中直接获取相关和期望的信息,一种文本挖掘的方法:主题模型(Topic Model ...
- 自然语言处理基础与实战(8)- 主题模型LDA理解与应用
本文主要用于理解主题模型LDA(Latent Dirichlet Allocation)其背后的数学原理及其推导过程.本菇力求用简单的推理来论证LDA背后复杂的数学知识,苦于自身数学基础不够,因此文中 ...
- 主题模型-LDA浅析
(一)LDA作用 传统判断两个文档相似性的方法是通过查看两个文档共同出现的单词的多少,如TF-IDF等,这种方法没有考虑到文字背后的语义关联,可能在两个文档共同出现的单词很少甚至没有,但两个文档是相似 ...
- LDA( Latent Dirichlet Allocation)主题模型 学习报告
1 问题描述 LDA由Blei, David M..Ng, Andrew Y..Jordan于2003年提出,是一种主题模型,它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一 ...
- [综] Latent Dirichlet Allocation(LDA)主题模型算法
多项分布 http://szjc.math168.com/book/ebookdetail.aspx?cateid=1&§ionid=983 二项分布和多项分布 http:// ...
- R语言︱LDA主题模型——最优主题数选取(topicmodels)+LDAvis可视化(lda+LDAvis)
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 笔者寄语:在自己学LDA主题模型时候,发现该模 ...
- 理解 LDA 主题模型
前言 gamma函数 0 整体把握LDA 1 gamma函数 beta分布 1 beta分布 2 Beta-Binomial 共轭 3 共轭先验分布 4 从beta分布推广到Dirichlet 分布 ...
- LDA(Latent Dirichlet allocation)主题模型
LDA是一种典型的词袋模型,即它认为一篇文档是由一组词构成的一个集合,词与词之间没有顺序以及先后的关系.一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成. 它是一种主题模型,它可以将文档 ...
随机推荐
- SpringMVC重定向传递参数
在SpringMVC的一个controller中要把参数传到页面,只要配置视图解析器,把参数添加到Model中,在页面用el表达式就可以取到.但是,这样使用的是forward方式,浏览器的地址栏是不变 ...
- 7.Python初窥门径(数据类型补充,操作及注意事项)
python(数据类型补充,转换及注意事项) 数据类型补充 str str.capitalize() 首字母大写 str.title() 每个单词首字母大写 str.count() 统计元素在str中 ...
- jQuery EasyUI/TopJUI创建树形表格下拉框
jQuery EasyUI/TopJUI创建树形表格下拉框 第一种方法(纯HTML创建) <div class="topjui-row"> <div class= ...
- Python-13-pass,del和exec
1.pass就是什么都不做 >>> pass >>> 2. 对于你不再使用的对象, Python通常会将其删除(因为没有任何变量或数据结构成员指向它) . &g ...
- Charles使用小结
charles,抓包神器,记录几个测试过程中常用的功能 连接同一局域网的开发机 域名跳转MapRemoteSetting 抓取Https接口 1.下载3.10以上破解版,按如下步骤安装 ...
- [Android]Android四大组件之Service总结
一.Service介绍 Service是Android中实现程序后台运行的解决方案,它非常适合用于去执行那些不需要和用户交互而且还要长期运行的task.Service的运行不需要依赖于任何用户界面,即 ...
- UVa 11168(凸包、直线一般式)
要点 找凸包上的线很显然 但每条线所有点都求一遍显然不可行,优化方法是:所有点都在一侧所以可以使用直线一般式的距离公式\(\frac{|A* \sum{x}+B* \sum{y}+C*n|}{\sqr ...
- Python基本的数据类型(补发)
python基本的数据类型 一.python的基本数据类型 int => 整数,主要用来进行数学运算 str ==> 字符串 可以用来保存少量数据并进行相应操作 bool ==> ...
- Linux Maven install
1 下载 maven : http://maven.apache.org/download.cgi2 解压 tar -xvf apache-maven-3.3.9-bin.tar.gz3 移到所需目录 ...
- Oracle使用SQL语句修改字段类型
Oracle使用SQL语句修改字段类型 1.如果表中没有数据 Sql代码 1 2 3 alter table 表名 modify (字段名1 类型,字段名2 类型,字段名3 类型.....) alt ...