POJ - 2411 Mondriaan's Dream（轮廓线dp）

Mondriaan's Dream

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways. 

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output

1
0
1
2
3
5
144
51205

题意：给出行列n，m，求用1*2的瓷砖铺满的方案数。

将当前行与上一行的情况预处理出来，

ps:行列全为奇一定是0，一点优化可以将大数作行，小数作列。

第一行和最后一行一定全为1，最后从第一行到最后一行递推即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define MAX 12
using namespace std;
typedef long long ll;

struct Node{
    int pre,now;
}node;
vector<Node> v;
ll dp[MAX][<<];

int n,m;
void dfs(int x,int pre,int now){
    if(x>m) return;
    if(x==m){
        node.pre=pre;
        node.now=now;
        v.push_back(node);
        return;
    }
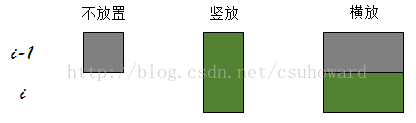
    dfs(x+,(pre<<)|,(now<<)|);   //横放
    dfs(x+,pre<<,(now<<)|);   //竖放
    dfs(x+,(pre<<)|,now<<);   //不放
}
int main()
{
    int i,j;
    while(scanf("%d%d",&n,&m)&&n+m){
        if((n*m)&){
            printf("0\n");
            continue;
        }
        if(n<m){
            int t=n;n=m;m=t;
        }
        v.clear();
        dfs(,,);
        memset(dp,,sizeof(dp));
        dp[][(<<m)-]=;
        for(i=;i<=n;i++){
            for(j=;j<v.size();j++){
                dp[i][v[j].now]+=dp[i-][v[j].pre];
            }
        }
        printf("%lld\n",dp[n][(<<m)-]);
    }
    return ;
}