【树形dp 最长链】bzoj1912: [Apio2010]patrol 巡逻

富有思维性的树形dp

Description

Input

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b， 表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input

8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6

Sample Output

11

HINT

10%的数据中，n ≤ 1000, K = 1； 
30%的数据中，K = 1； 
80%的数据中，每个村庄相邻的村庄数不超过 25； 
90%的数据中，每个村庄相邻的村庄数不超过 150； 
100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

---

题目分析

初看这题觉得毫无头绪，好像怎么也不能把它和最长链联系在一起。特别是新建的边必须经过一次的限制，让人一脸懵逼。

k=0

不过首先挖掘性质：显然的是，若只是树形图，路径最短为$2n-2$；并且实际上起点任意对于答案来说都是一样的。

k=1

然后我们来想一想$k=1$的情况。比如现在我们有一颗树长成这样：

然后我们现在添加一条边：

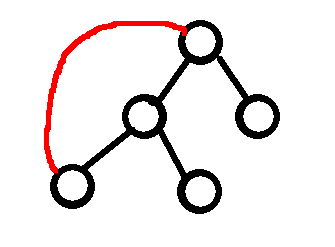
可以发现形成的环上，若环长度为$lens$，那么需要经过的路径就从$2*lens$变为了$lens+1$。并且对于其他节点来说，它们的花费是不改变的。

由此自然想到我们将最长链的首尾相连，就可以得到$k=1$时的答案。

k=2

有了k=1，扩展至k=2的思路大致相同。除了最长链形成的环，我们需要在树上另找一条次长链。

这里有一个技巧就是把最长链上的边权全都改为-1.引用CQzhangyu的一段话：

一开始想的是将直径拎出来，然后跑一个非常复杂的树形DP，但是看了题解。。。直接将直径上的所有边权值设为-1，再求一遍直径即可。正确性如何保证？如果这两条路径不相交，显然正确；如果相交，那么相当于将原路径拆成了两条。所以做法还是很巧妙的~

还有Coco_T的另一段话：

如果我们什么处理都没有，直接求一个次长链（次短路方法）， 
可能会和最长链重合，那么最长链上的一部分就会走两遍 
所以我们在求出最长链之后，把最长链上的边权赋为-1， 
这样再跑一个裸的直径就好了 
（这样就可以保证可以在新求出的直径中尽量少重合原先的直径）

其实感觉能够感性理解，但是好像依旧不甚明白……？

还有要注意的是：

     if (k==){
         mx = ;
         for (int i=s1[dir]; i!=-; i=s1[edges[i].y])
             edges[i].val = edges[i^].val = -;
         for (int i=s2[dir]; i!=-1; i=s1[edges[i].y])
             edges[i].val = edges[i^].val = -;
         dfs(, );
         ans = ans-mx+;
     }

这里第二部分的作用是，将dir的次长链的边权赋为-1.乍一眼看上去好像应该是for (int i=s2[dir]; i!=-1; i=s1[edges[i].y])，不过实际上次长链除了头上是s2，后面的路径走的都是其最大值。

 #include<bits/stdc++.h>
 const int maxn = ;

 struct Edge
 {
     int y,val;
     Edge(int a=, int b=):y(a),val(b) {}
 }edges[maxn<<];
 int n,k,mx,dir,ans;
 int edgeTot,nxt[maxn<<],head[maxn];
 int s1[maxn],s2[maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void addedge(int u, int v)
 {
     edges[++edgeTot] = Edge(v, ), nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = Edge(u, ), nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 int dfs(int now, int fa)
 {
     int mx1 = , mx2 = ;
     for (int i=head[now]; i!=-; i=nxt[i])
         if (edges[i].y!=fa){
             int tt = dfs(edges[i].y, now)+edges[i].val;
             if (tt > mx1)
                 mx2 = mx1, mx1 = tt, s2[now] = s1[now], s1[now] = i;
             else if (tt > mx2) mx2 = tt, s2[now] = i;
         }
     if (mx1+mx2 > mx) mx = mx1+mx2, dir = now;
     return mx1;
 }
 int main()
 {
     memset(head, -, sizeof head);
     memset(s1, -, sizeof s1);
     memset(s2, -, sizeof s2);
     n = read(), k = read();
     for (int i=; i<n; i++)
         addedge(read(), read());
     dfs(, );
     ans = *n-mx-;
     if (k==){
         mx = ;
         for (int i=s1[dir]; i!=-; i=s1[edges[i].y])
             edges[i].val = edges[i^].val = -;
         for (int i=s2[dir]; i!=-; i=s1[edges[i].y])
             edges[i].val = edges[i^].val = -;
         dfs(, );
         ans = ans-mx+;
     }
     printf("%d\n",ans);
     return ;
 }

END