【树论 倍增】51nod1709 复杂度分析

倍增与位运算有很多共性；这题做法有一点像「线段树上二分」和「线段树套二分」的关系。

给出一棵n个点的树(以1号点为根)，定义dep[i]为点i到根路径上点的个数。众所周知，树上最近公共祖先问题可以用倍增算法解决。现在我们需要算出这个算法精确的复杂度。我们定义计算点i和点j最近公共组先的精确复杂度为bit[dep[i]-dep[lca(i,j)]]+bit[dep[j]-dep[lca(i,j)]](bit[i]表示i在二进制表示下有多少个1，lca(i,j)表示点i和点j的最近公共祖先)。为了计算平均所需的复杂度为多少，请你帮忙计算任意两点计算最近公共组先所需复杂度的总和。

即计算 ∑n−1i=1∑nj=i+1 bit[dep[i]-dep[lca(i,j)]]+bit[dep[j]-dep[lca(i,j)]]

Input

第一行一个数n表示点数(1<=n<=100,000)
接下来n-1行每行两个数x,y表示一条边(1<=x,y<=n)

Output

一个数表示答案

Input示例

4
1 2
1 3
2 4

Output示例

8

---

题目分析

题目已经良心地把要求的式子给出来了。

自上向下的方法一

位运算计数题自然而然考虑按位计算贡献，注意到要求的是bit即个数，也就是说高位和低位是同性的。而这题略有特殊的是在于可以与倍增相结合做一些有趣的事情。

由于边权为1，倍增预处理的到祖先节点的二的幂次，就是到祖先节点的距离的二进制拆分。

那么就可以先枚举logn数量的每一种2^i深度d，再枚举所有n个点。对于每一个枚举的点，统计与它相距2^{d-1}<dis≤2^d的祖先节点的贡献。

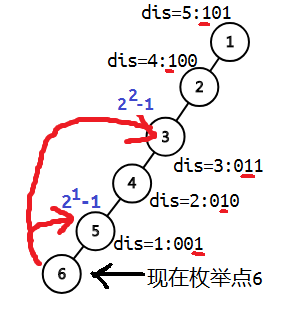
直观来说就是这张图。主要代码是这样的：

     for (int d=; d<; d++)
     {
         memset(w, , sizeof w);
         for (int ix=; ix<=n; ix++)
         {
             int i = chain[ix];　　　　//树的dfs序，因为要自上向下做
             w[i] = tot[f[i][d+]]-tot[f[i][d]];
             if (dep[i] > <<(d+)) w[i] += w[fa[f[i][d+]]];
             ans += w[i];
         }
     }

如果想要更加程式化的描述，见51Nod1709 复杂度分析这篇博客。

 #include<bits/stdc++.h>
 const int maxn = ;

 int n,w[maxn];
 long long ans;
 int chain[maxn],tot[maxn],chTot;
 int f[maxn][],dep[maxn],fa[maxn];
 int edgeTot,edges[maxn<<],nxt[maxn<<],head[maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void addedge(int u, int v)
 {
     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 void dfs(int x, int fat)
 {
     f[x][] = x, f[x][] = fa[x] = fat, dep[x] = dep[fat]+;
     tot[x] = , chain[++chTot] = x;
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (v!=fat){
             dfs(v, x);
             tot[x] += tot[v];
         }
     }
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read();
     for (int i=; i<n; i++) addedge(read(), read());
     dfs(, );
     for (int j=; j<=; j++)
         for (int i=; i<=n; i++)
             f[i][j] = fa[f[f[i][j-]][j-]];
     for (int d=; d<; d++)
     {
         memset(w, , sizeof w);
         for (int ix=; ix<=n; ix++)
         {
             int i = chain[ix];
             w[i] = tot[f[i][d+]]-tot[f[i][d]];
             if (dep[i] > <<(d+)) w[i] += w[fa[f[i][d+]]];
             ans += w[i];
         }
     }
     printf("%lld\n",ans);
     return ;
 }

自上向下的方法二

在这里给出一种O(nlog)的做法。记录每个节点的fa和子树size。
枚举一个k，用s[i]表示节点i子树内和i距离小于 2^k 大于等于2^k−1的节点数，v[i]表示节点i子树内和i距离小于 2^k 大于等于 2^k−1 的节点和i距离的bit总数,now[i]表示i向上的第 2^k−1 个祖先。
每次倍增计算每个点子树内和它距离小于 2^k 大于等于 2^k−1 的点的距离对答案的贡献即可。

@hzq84621　　自http://www.51nod.com/question/index.html#!questionId=1546

【博客园抽风没法正常显示数学公式我也很难受啊】

END