欧拉函数φ(x)简要介绍及c++实现

我还是很喜欢数论，从此吃喝不问，就此沉沦。

欧拉函数φ(x)的值为在[1,x)的区间内与x互质的数的个数

通式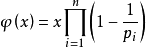：    其中p1, p2……pn为x的所有质因数，x是不为0的整数。φ(1)=1。

注意：每种质因数只一个。 比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4

介绍几个性质：

1.若n是质数p的k次幂，则，因为除了p的倍数外，其他数都跟n互质。

2.积性函数——若m,n互质，。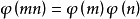

3.当n为质数时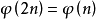， , 其实与上述类似。

4.若n为质数则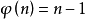, 这个挺重要的。

5.一个数的所有质因子之和是φ(n)*n/2。

 //用通式算的
 int euler(int n){ //返回euler(n)
     int res=n,a=n;
     for(int i=;i*i<=a;i++){
         if(a%i==){
             res=res/i*(i-);//先进行除法是为了防止中间数据的溢出
             while(a%i==) a/=i;
         }
     }
     if(a>) res=res/a*(a-);
     return res;
 }

 //筛选法打欧拉函数表
 #define Max 1000001
 int euler[Max];
 void Init(){
      euler[]=;
      for(int i=;i<Max;i++)
        euler[i]=i;
      for(int i=;i<Max;i++)
         if(euler[i]==i)
            for(int j=i;j<Max;j+=i)
               euler[j]=euler[j]/i*(i-);//先进行除法是为了防止中间数据的溢出
 }
 */