算法设计与分析-HomeWork

ex1(p20)

代码如下：

 import random

 def Darts(n):
     k=0
     i=1
     while i<=n:
         x=random.uniform(0,1)
         #y=random.uniform(0,1)
         y=x
         if(x**2+y**2<=1):
             k+=1
         i+=1
     return 4*k/n

 print(Darts(10000000))
 print(Darts(100000000))
 print(Darts(100000000))

结果如下：

物理意义：计算2*sqrt（2）  #如果结果输出的是2*k/n，则计算的是无理数sqrt（2）的近似值

ex2(p23)

代码如下：

 import random
 import math

 def F(x):
     return math.sqrt(1-x**2)

 def CalPI(n):
     k=0
     i=1
     while i<=n:
         i+=1
         x=random.uniform(0,1)
         y=random.uniform(0,1)
         if (y<=F(x)):
             k+=1
     return 4*k/n

 print("when n=10000000,PI=%.10f"%CalPI(10000000))
 print("when n=100000000,PI=%.10f"%CalPI(100000000))
 print("when n=1000000000,PI=%.10f"%CalPI(1000000000))

结果如下：

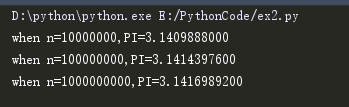
ex3（p23）

代码如下：

 import random
 import math

 def F(x):
     return x-1

 def CalCalculus(a,b,c,d,n,function):
     k_positive=0
     k_negtive=0
     i=1
     while i<=n:
         i+=1
         x=random.uniform(a,b)
         y=random.uniform(c,d)
         if (y>=0 and y<=function(x)):
             k_positive+=1
         elif(y<0 and y>function(x)):
             k_negtive+=1
     return (b-a)*(d-c)*(k_positive-k_negtive)/n

 if __name__=="__main__":
     function=F
     str=input("please input a,b,c,d:");
     ceof=list(str.split(" "))
     ceof=[int(i) for i in ceof]
     print(ceof)
     print("when n=1000000,res=%.10f"%CalCalculus(ceof[0],ceof[1],ceof[2],ceof[3],1000000,function))
     print("when n=10000000,res=%.10f"%CalCalculus(ceof[0],ceof[1],ceof[2],ceof[3],10000000,function))
     print("when n=100000000,res=%.10f"%CalCalculus(ceof[0],ceof[1],ceof[2],ceof[3],100000000,function))

结果如下：

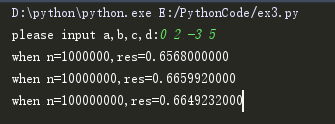
p24 Ex4

ex4(p36)

代码如下：

 # -*- coding: utf-8 -*-
 """
 __title__ = ''
 __author__ = 'jing'
 __mtime__ = '2017/9/20'
 # code is far away from bugs with the god animal protecting
     I love animals. They taste delicious.
               ┏┓      ┏┓
             ┏┛┻━━━┛┻┓
             ┃      ☃      ┃
             ┃  ┳┛  ┗┳  ┃
             ┃      ┻      ┃
             ┗━┓      ┏━┛
                 ┃      ┗━━━┓
                 ┃  神兽保佑    ┣┓
                 ┃　永无BUG！   ┏┛
                 ┗┓┓┏━┳┓┏┛
                   ┃┫┫  ┃┫┫
                   ┗┻┛  ┗┻┛
 """
 import random
 import math

 def CalSetCount(setN):
     setTemp=set()
     k=0
     a=random.choice(setN)
     while a not in setTemp:
         k+=1
         setTemp.add(a)
         a = random.choice(setN)
     return k

 if __name__=="__main__":
     n=int(input("please enter n(the numbers of set):"))
     while n!=0:
         setN=range(0,n)
         i=0
         kList=[]
         while i<1000:
             i+=1
             kList.append(CalSetCount(setN))
         print("The estimated value of n is %.f"%(2.0*((sum(kList)/1000)**2)/math.pi))
         n = int(input("please enter n(the numbers of set):"))

结果如下：

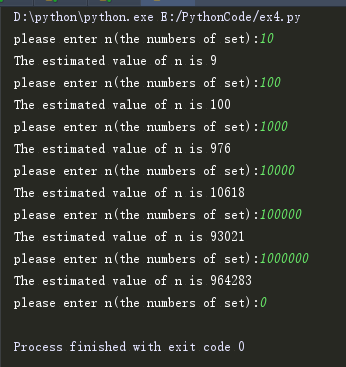
随着n值的增大，误差存在着波动性，但整体趋势是越来越小的

p54

p64 ex

 import random

 count=1

 def Search(val,ptr,x,i):
     global  count
     count=1
     while x>val[i]:
         i=ptr[i]
         count=count+1
     return i

 def A(val,ptr,x,head):
     return Search(val,ptr,x,head)

 def B(val,ptr,x,head):
     i=head
     max=val[i]
     for j in range(4):
         y=val[j]
         if max<y and y<=x:
             i=j
             max=y
     return Search(val,ptr,x,i)

 def C(val,ptr,x,head):
     i=head
     max=val[i]
     for k in range(4):
         j=random.randint(0,15)
         y=val[j]
         if max<y and y<=x:
             i=j
             max=y
     return Search(val,ptr,x,i)

 def D(val,ptr,x,head):
     i=random.randint(0,15)
     y=val[i]
     if x<y:
         return Search(val,ptr,x,head)
     elif x>y:
         return Search(val,ptr,x,ptr[i])
     else:
         return i

 val=[5,7,3,0,4,11,17,14,9,20,21,25,23,30,34,31]
 ptr=[1,8,4,2,0,7,9,6,5,10,12,13,11,15,-1,14] #the maxnum's index equats to -1

 head=3
 x=11
 print("C:x=11's position is %d.Compared %d times\n"%(C(val,ptr,x,head),4+count))
 print("A:x=11's position is %d.Compared %d times\n"%(A(val,ptr,x,head),count))
 print("B:x=11's position is %d.Compared %d times\n"%(B(val,ptr,x,head),4+count))
 print("D:x=11's position is %d.Compared %d times\n"%(A(val,ptr,x,head),count))

 x=30
 print("C:x=30's position is %d.Compared %d times\n"%(C(val,ptr,x,head),4+count))
 print("A:x=30's position is %d.Compared %d times\n"%(A(val,ptr,x,head),count))
 print("B:x=30's position is %d.Compared %d times\n"%(B(val,ptr,x,head),4+count))
 print("D:x=30's position is %d.Compared %d times\n"%(A(val,ptr,x,head),count))