[题解]luogu_P2155_BZOJ_2186沙拉公主的困惑

题意求1~N！中与M！互质的数的个数，

首先证明gcd（a，b）=1时gcd（a-kb，b）=1

gcd（a，b）=1

gcd（a%b，b）=1

gcd（a-kb，b）=1

即a-kb与b互质

这样由于n！一定是m！的倍数，所以如果把n！分成很多段m！的和：1~m！，m！~2m！......

对于每一段的每个答案gcd（x，m！）=1时，也有gcd（x+km！，m！）=1

所以每段的答案都是一样的

这样答案变成了n！/m！ * phi（m！）

对于phi（m！）用计算公式展开：

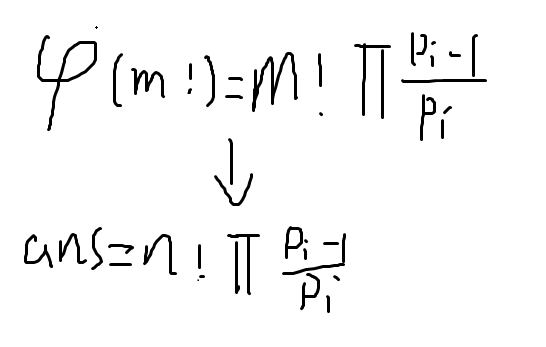
这里可以递推出相关的东西和逆元之类的，然而其实还可以继续简化运算

其实也只是不用求逆元了而已吧

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
const int maxn=;
int n,m;
ll mod;
ll fac[maxn],f1[maxn],f2[maxn];
int prime[maxn];
bool ck[maxn];
void init(){
    int tot=;
    memset(ck,,sizeof(ck));
    ck[]=ck[]=;
    for(int i=;i<=maxn;i++){
        if(!ck[i])prime[++tot]=i;
        for(int j=;j<=tot;j++){
            if(i*prime[j]>maxn)break;
            ck[i*prime[j]]=;
            if(i%prime[j]==)break;
        }
    }
}
ll qpow(ll a,ll b){
    ll base=a,ans=;
    while(b){
        if(b&)ans=(ans*base)%mod;
        base=(base*base)%mod;
        b>>=;
    }
    return ans%mod;
}
int main(){
    int T;
    scanf("%d%lld",&T,&mod);
    init();
    fac[]=f1[]=f2[]=1ll;
    for(int i=;i<maxn;i++){
        fac[i]=fac[i-]*i%mod;
        if(!ck[i])
        f1[i]=f1[i-]*(i-)%mod,f2[i]=f2[i-]*i%mod;
        else
        f1[i]=f1[i-],f2[i]=f2[i-];
    }
    while(T--){
        scanf("%d%d",&n,&m);
        printf("%lld\n",((fac[n]*f1[m])%mod)*qpow(f2[m],mod-)%mod);
    }
}