dp优化1——sgq（单调队列）

该文是对dp的提高（并非是dp入门，dp入门者请先参考其他文章）

有时候dp的复杂度也有点大。。。会被卡。

这几次blog大多数会讲dp优化。

回归noip2017PJT4.（题目可以自己去百度）。就是个很好的案例。那题是个二分套dp如果dp不优化复杂度O(n^2logn)还能拿60分（CCF太仁慈了，如果是我直接给10分）。

正解加上个单调队列（其实是sliding window）O(nlogn)

我们发现，此类dp是这样的

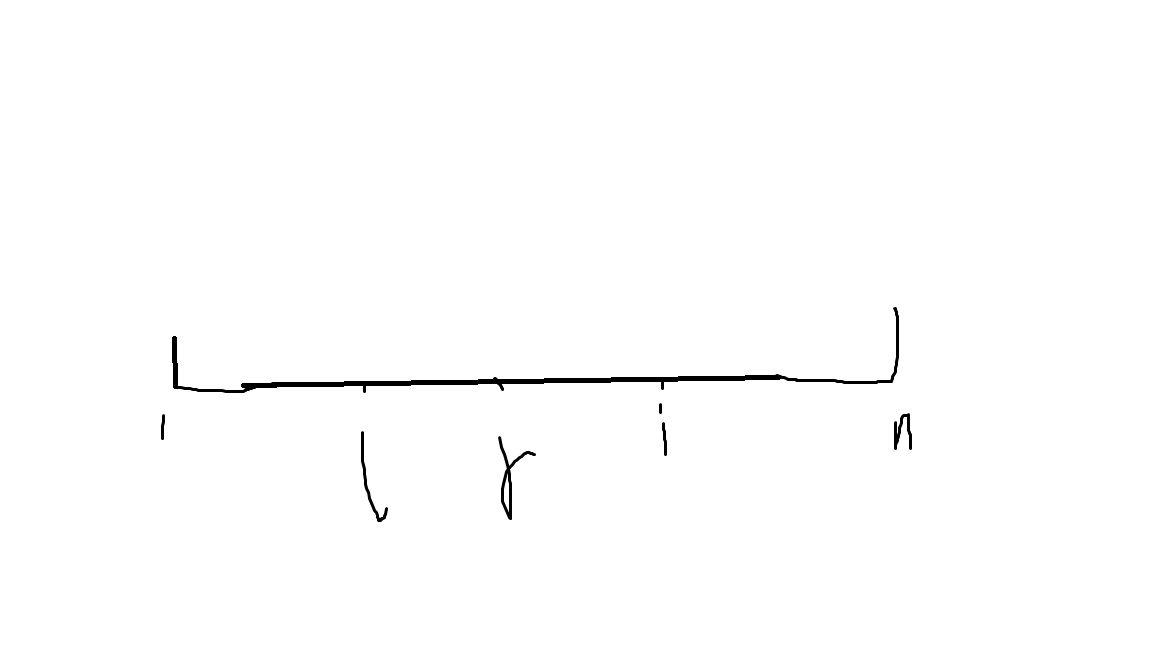
状态i是由[l,r]转移过来的。且i在向右移动的过程中，[l,r]一定会跟着往右移，那不就是单调队列吗！！！

至于单调队列都不会的，我在这给一句解释———如果一个人比你小，还比你强，那你就永远比不过他了--chen_zhe大佬

其实是这样的——能转移到i的窗口[l,r]在向右移动的过程中，我们加一个队列，队首的dp值最优，在r向右移动时，遇到一个状态t

写个伪代码

while(队列不空&&t的dp值由于队尾值)弹出队尾元素；将t插入队尾

别忘了，l还要向右移动，右移会导致一些状态离开队列，需要在原队列删除。

OK接下来看例题：

多重背包n个物体，每个numi个，每个物品右价值和重量，求重量不超过m的最大价值（不会o(n^2m)请自行百度，改文不介绍过于基础的dp）。

您会说一句，这种水题我30s切。结果切完后就30分。。。。

一拍脑袋，二进制优化-》O(nmlogn)（将numi分解二进制，再用01做）

结果毒瘤的数据结构大师lxl成功卡掉了您的log(送你《凉凉》x1)

看来只能用O(nm)的做法，先写下dp转移方程

dp[i][j]表示前i个物体，限制重量为j的最大价值

dp[i][j]=max(dp[i-1][j-k*w[i]]+v[i]*k)(0<=k<=num[i])

状压：dp[j]=max(dp[j-k*w[i]]+v[i]*k)

我们先瞎搞：

在i和j都确定的情况下：

设：

n*w[i]+p=j p=j%w[i];

j/w[i]=n(注意是整除)

原方程变为dp[j]=max(dp[j%w[i]+k*w[i]]-k*w[i])+n*w[i]（2）

聪明的你一定会了。

这个方程的k与原来的K不同（为区分下文将原来的K大写）

如果你自己推过（2），您会发现k=n-K

这样可以搞出k的范围

0<=n-k<=num[i]

n-num[i]<=k<=n

在j%w【i】不变时max(dp[j%w[i]+k*w[i]]-k*w[i])只与k有关，爽歪歪~~ 单调队列喽。

不懂再想想这张图(important)

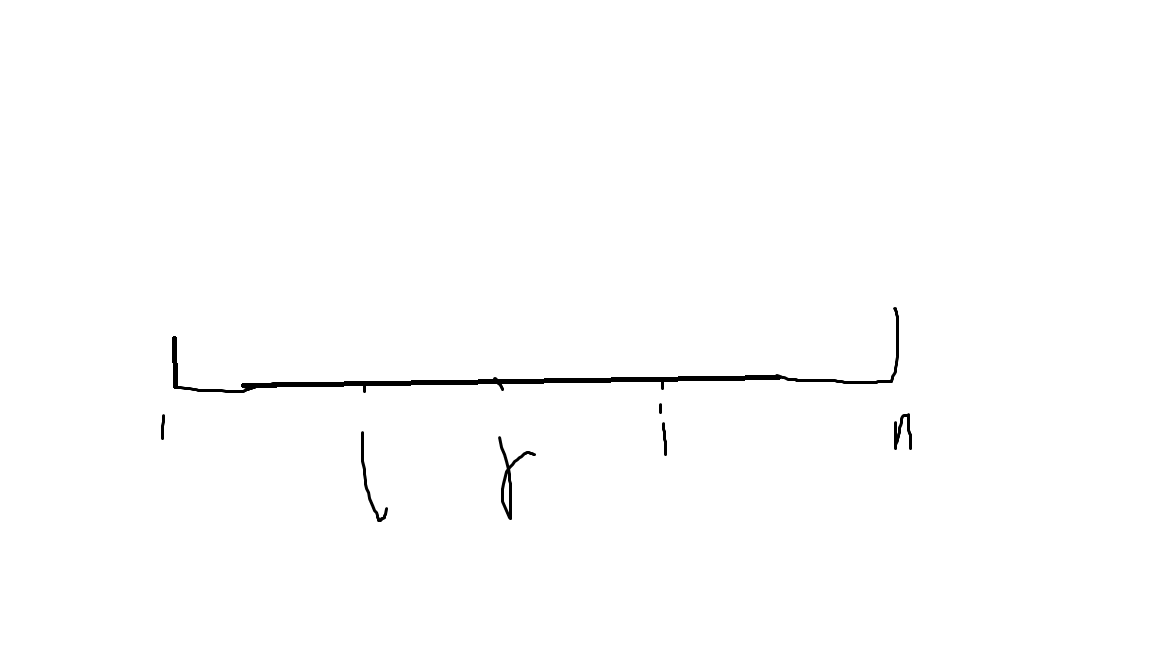
没例题总不行！！例题是hdu1171（多重背包裸题）。但出题者非常善良，O(n^2m)也给过了。

单调队列79MS，纯dp1092MS

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
][],v[],num[];
],l,r,n;
int main(){//freopen("in.txt","r",stdin);freopen("o1.txt","w",stdout);
    ){
        memset(dp,,,,sizeof(num));
        l=r=;
        ,j;
        ;i<=n;++i)scanf("%d%d",&v[i],&num[i]),sum+=v[i]*num[i];
        ,p,ans=;
        ;i<=n;++i){
            ;p<v[i];++p){
                int kl,kr;
                l=r=;l=;q[++r]=;
                for(j=p;j<=m;j+=v[i]){
                    int pre=kr;
                    kl=max(j/v[i]-num[i],),kr=j/v[i];
                    while(l<=r && (q[l]<kl || q[l]>kr))++l;
                    ;k<=kr;++k){
                        ^][j%v[i]+q[r]*v[i]]-q[r]*v[i]<dp[i%^][j%v[i]+k*v[i]]-k*v[i])--r;
                        q[++r]=k;
                    }
                    dp[i%][j]=dp[i%^][j%v[i]+q[l]*v[i]]-q[l]*v[i]+(j/v[i])*v[i];
                    ans=max(ans,dp[i%][j]);
                }
            }
        }
        printf("%d %d\n",sum-ans,ans);
    }
}