HMM隐马尔可夫模型来龙去脉(一)
目录
隐马尔可夫模型HMM学习导航
隐马尔可夫模型HMM学习导航
NLP学习记录,这一章从概率图模型开始,学习常见的图模型具体的原理以及实现算法,包括了有向图模型:贝叶斯网络(BN)、(隐)马尔可夫模型(MM/HMM),无向图模型:马尔可夫网络(MN)、条件随机场(CRF)。学习前提条件需要一定的概率论与数理统计知识,里面许多方法都是概率统计知识。
图模型框架:
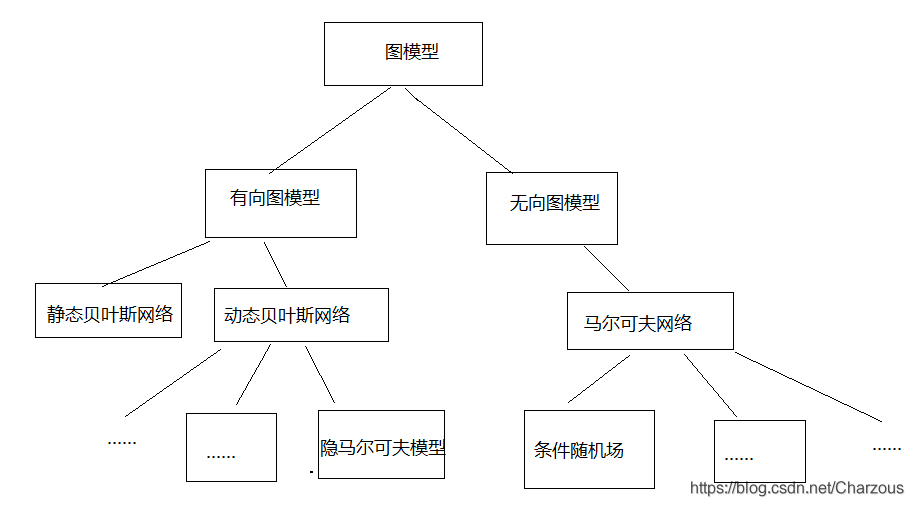
一、认识贝叶斯网络
1、概念原理介绍
贝叶斯网络是一种基于概率推理的数学模型,属于有向无环图,理论基础就是我们熟悉的贝叶斯公式。
公式中,事件Bi的概率为P(Bi),事件Bi已发生条件下事件A的概率为P(A│Bi),事件A发生条件下事件Bi的概率为P(Bi│A),公式分母就是全概率公式。
构造贝叶斯网络任务复杂,包括表示、推断、学习三个方面的问题。这里就简单介绍。
- 表示:某个随机变量集合
上联合概率分布P,贝叶斯网络的表示就是在随机变量仅有两种取值的简单情况下,对
种不同取值的联合概率分布进行说明,可以看出,这是计算量巨大的任务。
- 推断:贝叶斯网络是变量及其关系的完整模型,可以从观察到或已知的变量推断另一些变量的变化,这种根据已知的证据计算变量的后验分布称为概率推理。
- 学习:指的是BN中参数的学习,目的是决定变量之间的关联量化关系(依存强度估计)。参数学习方法包括:最大似然估计法、最大后验概率法、期望最大化法和贝叶斯估计法(使用最多)。
2、举例解析
从前面一片理论介绍和概念中,似乎很不直观,还没理解贝叶斯网络到底是什么,现在我们通过简单例子更加直观深刻地去认识。
假设一篇关于南海岛屿的新闻(News),新闻里可能包含关于介绍南海岛屿历史的内容(History),还有介绍旅游风光的内容(Sightseeing)。现在对此构造建立一个简单的贝叶斯网络。
现在用N、H、S表示这3个事件,每个事件存在两种可能,记为T(包含/是)、F(不包含/不是),通过假设概率建模:
| New | |
| T | F |
| 0.2 | 0.8 |
| Sightseeing | ||
| News | T | F |
| F | 0.4 | 0.6 |
| T | 0.1 | 0.9 |
| History | |||
| Sightseeing | News | T | F |
| F | F | 0.5 | 0.5 |
| F | T | 0.3 | 0.7 |
| T | F | 0.8 | 0.2 |
| T | T | 0.4 | 0.6 |
一个简单的贝叶斯网络:

上面表格枚举了所有可能的情况概率分布,现在根据表格内容和建立的BN图关系,三个事件的联合概率:
即 .
给出一个问题:如果一篇新闻中含有南海岛屿历史相关的内容,那么该新闻是关于南海新闻的可能性是多少呢?
显然,模型能够解决这个问题,根据题意我们得出,就是计算 H=T的情况下 N=T 的条件概率 。
进一步求解得到
现在直接代入表格的数据,按H,S,N顺序,分子为TTT+TFT,分母TTT+TFT+TTF+TFF. 由此计算得到:
.
二、马尔可夫模型
1、概念原理介绍
马尔可夫模型是一个可见的过程,隐马尔可夫模型则是将随机事件的状态转移过程屏蔽,所以学习马尔可夫模型作为前提。
马尔可夫模型(Markov Model)描述了一种随机函数,是随着时间不断变化的过程。换言之,我们观察到每个随机变量序列并不是相互独立的,而是依赖于其前面序列的状态。
2、举例解析
假设系统有N个状态
, 一个随机序列
, t 时刻状态
,那它的概率如何计算呢?
计算t时刻状态的概率需要给出前面t-1个状态的关系,概率表示为:
,相当于求解条件概率。
对于马尔可夫模型来说,有这样的特定条件,系统t时刻的状态只与其在时间t-1状态相关,所以表示为如下,称为一阶马尔可夫链。
.
进而由上面的是公式得到一个随机过程表示,构成状态转移矩阵。
, 满足
. 可见N个状态可以构成N*N个状态转移概率。
下面用更加直观例子解析马尔可夫模型。
假设一段文字中有三类词性:名词、动词、形容词。这三类词性的出现可以表示为马尔可夫模型的三个状态,描述为:
状态a:名词
状态b:动词
状态c:形容词
假设转移矩阵如下:
各状态关系,每个状态所有发射弧概率之和为1
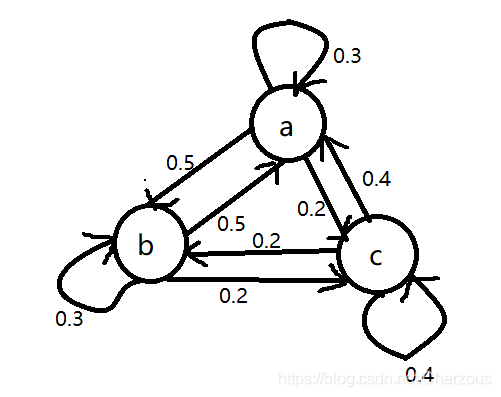
根据此模型M,计算某个句子序列词性出现顺序 O = "名动形名"的概率:
三、隐马尔可夫模型
1、概念原理介绍
在前面马尔可夫模型,每个状态都是可见的。而隐马尔可夫模型,就是将这状态序列隐蔽,变为状态转移过程不可见。HMM是一个双重随机过程。它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。
2、举例解析
一个暗室里面有N个口袋,每个口袋有M个不同颜色小球。这个过程包括实验者和观察者。实验者每次根据某个概率分布随机选取一个口袋,再根据某个概率分布从这个口袋中取出一个小球,并向观察者展示该球的颜色。
我们理解一下这个过程,观察者只能知道每次取出球的颜色序列,而不知是从哪个口袋取出的,这个口袋序列的状态转移只有暗室里的实验者知道。所以,观察者的任务就是根据可观察序列(球颜色序列)来推断出隐藏的转移过程。
由此,总结出一个HMM有以下组成:
- 模型状态数目N(如例子中的口袋数量)
- 每个状态可能输出的不同符号数目M(一个口袋不同颜色球的数目)
- 状态转移矩阵A={
} (
是实验者从一口袋 i 转向口袋 j 的概率)。
,
。
- 观察到符号的概率(符号发射概率)分布矩阵B={
} (表示实验者从第j个袋取出第k种颜色的球)。
- 初始状态概率分布π。
四、隐马尔可夫模型简单实现
初始化状态数目n和样本数量,得到初始概率:
import numpy as np
from hmmlearn import hmm
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.metrics.pairwise import pairwise_distances_argmin np.random.seed(28)
n = 5 # 隐状态数目
n_samples = 500 # 样本数量
pi = np.random.rand(n)
pi /= pi.sum()
print('初始概率:')
print(pi)

计算转移矩阵:
A = np.random.rand(n, n)
mask = np.zeros((n, n), dtype=np.bool)
mask[0][1] = mask[0][4] = True
mask[1][0] = mask[1][2] = True
mask[2][1] = mask[2][3] = True
mask[3][2] = mask[3][4] = True
mask[4][0] = mask[4][3] = True
A[mask] = 0
for i in range(n):
A[i] /= A[i].sum()
print('转移概率:')
print(A)
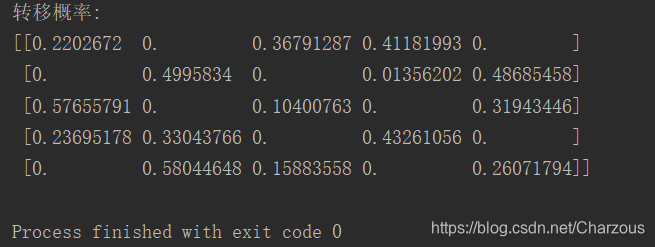
给定均值和方差:
# 给定均值
means = np.array(((30, 30, 30), (0, 50, 20), (-25, 30, 10),
(-15, 0, 25), (15, 0, 40)), dtype=np.float)
for i in range(n):
means[i, :] /= np.sqrt(np.sum(means ** 2, axis=1))[i]
covars = np.empty((n, 3, 3))
for i in range(n):
covars[i] = np.diag(np.random.rand(3) * 0.02 + 0.001)
产生模拟数据、模型构建及估计参数:
# 产生对应的模拟数据
model = hmm.GaussianHMM(n_components=n, covariance_type='full')
model.startprob_ = pi
model.transmat_ = A
model.means_ = means
model.covars_ = covars
sample, labels = model.sample(n_samples=n_samples, random_state=0) # 模型构建及估计参数
model = hmm.GaussianHMM(n_components=n, n_iter=10)
model.fit(sample)
y = model.predict(sample)
np.set_printoptions(suppress=True)
# print('##估计初始概率:')
# print(model.startprob_)
# print('##估计转移概率:')
# print(model.transmat_)
# print('##估计均值:\n')
# print(model.means_)
# print('##估计方差:\n')
# print(model.covars_)
根据类别信息更改顺序:
# 根据类别信息更改顺序
order = pairwise_distances_argmin(means, model.means_, metric='euclidean')
# print(order)
pi_hat = model.startprob_[order]
A_hat = model.transmat_[order]
A_hat = A_hat[:, order]
means_hat = model.means_[order]
covars_hat = model.covars_[order]
change = np.empty((n, n_samples), dtype=np.bool)
for i in range(n):
change[i] = y == order[i]
for i in range(n):
y[change[i]] = i
acc = np.mean(labels == y) * 100
print('准确率:%.2f%%' % acc)

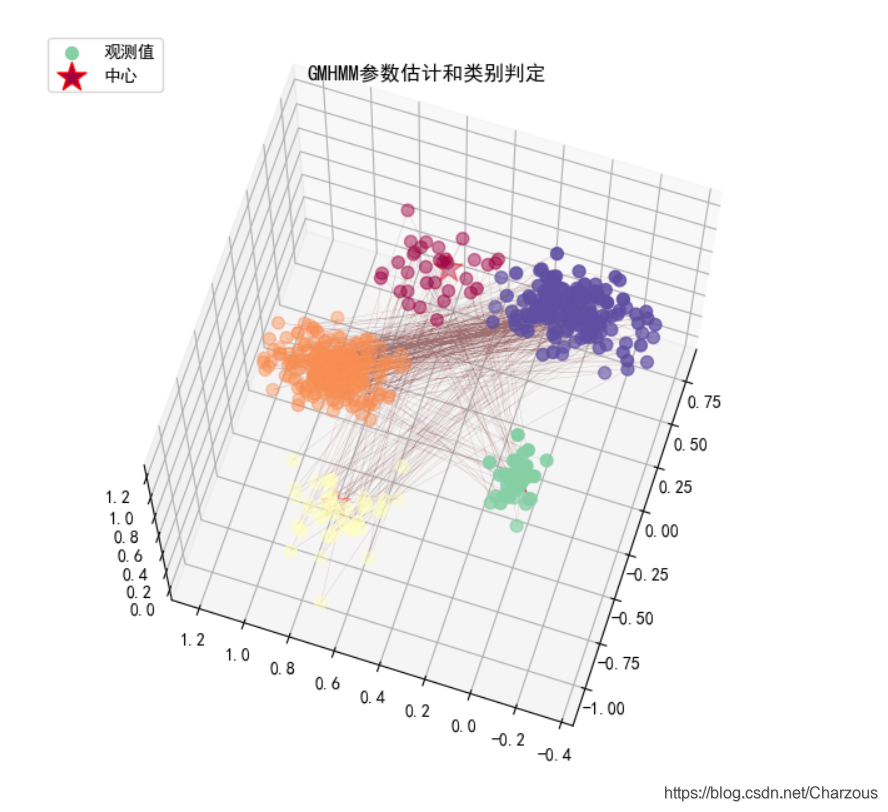
3D画图分类结果:


mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(8, 8), facecolor='w')
ax = fig.add_subplot(111, projection='3d') #
colors = plt.cm.Spectral(np.linspace(0, 1, n))
ax.scatter(sample[:, 0], sample[:, 1], sample[:, 2], s=50, c=labels,
cmap=plt.cm.Spectral, marker='o', label=u'观测值', depthshade=True)
plt.plot(sample[:, 0], sample[:, 1], sample[:, 2], lw=0.1, color='#A07070')
colors = plt.cm.Spectral(np.linspace(0, 1, n))
ax.scatter(means[:, 0], means[:, 1], means[:, 2], s=300, c=colors,
edgecolor='r', linewidths=1, marker='*', label=u'中心') x_min, y_min, z_min = sample.min(axis=0)
x_max, y_max, z_max = sample.max(axis=0)
x_min, x_max = expand(x_min, x_max)
y_min, y_max = expand(y_min, y_max)
z_min, z_max = expand(z_min, z_max)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.set_zlim((z_min, z_max))
plt.legend(loc='upper left')
plt.grid(True)
plt.title(u'GMHMM参数估计和类别判定', fontsize=12)
plt.show()
五、完整代码


import numpy as np
from hmmlearn import hmm
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
from sklearn.metrics.pairwise import pairwise_distances_argmin def expand(a, b):
return 1.05 * a - 0.05 * b, 1.05 * b - 0.05 * a np.random.seed(28)
n = 5 # 隐状态数目
n_samples = 500 # 样本数量
pi = np.random.rand(n)
pi /= pi.sum()
# print('初始概率:')
# print(pi) A = np.random.rand(n, n)
mask = np.zeros((n, n), dtype=np.bool)
mask[0][1] = mask[0][4] = True
mask[1][0] = mask[1][2] = True
mask[2][1] = mask[2][3] = True
mask[3][2] = mask[3][4] = True
mask[4][0] = mask[4][3] = True
A[mask] = 0
for i in range(n):
A[i] /= A[i].sum()
# print('转移概率:')
# print(A) # 给定均值
means = np.array(((30, 30, 30), (0, 50, 20), (-25, 30, 10),
(-15, 0, 25), (15, 0, 40)), dtype=np.float)
for i in range(n):
means[i, :] /= np.sqrt(np.sum(means ** 2, axis=1))[i]
# print(means) # 给定方差
covars = np.empty((n, 3, 3))
for i in range(n):
covars[i] = np.diag(np.random.rand(3) * 0.02 + 0.001) # np.random.rand ∈[0,1)
# print(covars) # 产生对应的模拟数据
model = hmm.GaussianHMM(n_components=n, covariance_type='full')
model.startprob_ = pi
model.transmat_ = A
model.means_ = means
model.covars_ = covars
sample, labels = model.sample(n_samples=n_samples, random_state=0) # 模型构建及估计参数
model = hmm.GaussianHMM(n_components=n, n_iter=10)
model.fit(sample)
y = model.predict(sample)
np.set_printoptions(suppress=True) # 根据类别信息更改顺序
order = pairwise_distances_argmin(means, model.means_, metric='euclidean')
# print(order)
pi_hat = model.startprob_[order]
A_hat = model.transmat_[order]
A_hat = A_hat[:, order]
means_hat = model.means_[order]
covars_hat = model.covars_[order]
change = np.empty((n, n_samples), dtype=np.bool)
for i in range(n):
change[i] = y == order[i]
for i in range(n):
y[change[i]] = i
acc = np.mean(labels == y) * 100
print('准确率:%.2f%%' % acc) mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(8, 8), facecolor='w')
ax = fig.add_subplot(111, projection='3d') #
colors = plt.cm.Spectral(np.linspace(0, 1, n))
ax.scatter(sample[:, 0], sample[:, 1], sample[:, 2], s=50, c=labels,
cmap=plt.cm.Spectral, marker='o', label=u'观测值', depthshade=True)
plt.plot(sample[:, 0], sample[:, 1], sample[:, 2], lw=0.1, color='#A07070')
colors = plt.cm.Spectral(np.linspace(0, 1, n))
ax.scatter(means[:, 0], means[:, 1], means[:, 2], s=300, c=colors,
edgecolor='r', linewidths=1, marker='*', label=u'中心') x_min, y_min, z_min = sample.min(axis=0)
x_max, y_max, z_max = sample.max(axis=0)
x_min, x_max = expand(x_min, x_max)
y_min, y_max = expand(y_min, y_max)
z_min, z_max = expand(z_min, z_max)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.set_zlim((z_min, z_max))
plt.legend(loc='upper left')
plt.grid(True)
plt.title(u'GMHMM参数估计和类别判定', fontsize=12)
plt.show()
六、结语
通过这篇学习记录,我们初步认识了HMM隐马尔可夫模型的具体内部逻辑,另外举例解析和最后python简单实现一个例子,更直观的去理解什么是HMM,它是如何工作的。到这里可能觉得代码实现还有部分陌生的方法,因为HMM是一个比较复杂的任务,除了本文简单入门,HMM还需要解决三个基本问题,认真阅读的朋友会看到在代码中有所体现:估计问题、序列问题和训练问题(参数估计)。
这些问题等待接下来学习之后再来具体介绍,期待下一篇更核心的内容解析。
参考资料:《统计自然语言处理》、https//www.jianshu.com/p/083c8dfb9f0a
我的博客园:
我的CSDN: 原创 隐马尔可夫模型(HMM)来龙去脉(一)
HMM隐马尔可夫模型来龙去脉(一)的更多相关文章
- HMM隐马尔可夫模型来龙去脉(二)
目录 前言 预备知识 一.估计问题 1.问题推导 2.前向算法/后向算法 二.序列问题 1.问题推导 2.维特比算法 三.参数估计问题 1.问题推导 2.期望最大化算法(前向后向算法) 总结 前言 H ...
- HMM隐马尔可夫模型(词语粘合)
HMM用于自然语言处理(NLP)中文分词,是用来描述一个含有隐含未知参数的马尔可夫过程,其目的是希望通过求解这些隐含的参数来进行实体识别,说简单些也就是起到词语粘合的作用. HMM隐马尔可夫模型包括: ...
- HMM隐马尔科夫模型
这是一个非常重要的模型,凡是学统计学.机器学习.数据挖掘的人都应该彻底搞懂. python包: hmmlearn 0.2.0 https://github.com/hmmlearn/hmmlearn ...
- 机器学习-HMM隐马尔可夫模型-笔记
HMM定义 1)隐马尔科夫模型 (HMM, Hidden Markov Model) 可用标注问题,在语音识别. NLP .生物信息.模式识别等领域被实践证明是有效的算法. 2)HMM 是关于时序的概 ...
- 自然语言处理(1)-HMM隐马尔科夫模型基础概念(一)
隐马尔科夫模型HMM 序言 文本序列标注是自然语言处理中非常重要的一环,我先接触到的是CRF(条件随机场模型)用于解决相关问题,因此希望能够对CRF有一个全面的理解,但是由于在学习过程中发现一个算法像 ...
- HMM 隐马尔科夫模型
参考如下博客: http://www.52nlp.cn/itenyh%E7%89%88-%E7%94%A8hmm%E5%81%9A%E4%B8%AD%E6%96%87%E5%88%86%E8%AF%8 ...
- HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模 ...
- 隐马尔可夫模型(Hidden Markov Model)
隐马尔可夫模型(Hidden Markov Model) 隐马尔可夫模型(Hidden Markov Model, HMM)是一个重要的机器学习模型.直观地说,它可以解决一类这样的问题:有某样事物存在 ...
- 一文搞懂HMM(隐马尔可夫模型)
什么是熵(Entropy) 简单来说,熵是表示物质系统状态的一种度量,用它老表征系统的无序程度.熵越大,系统越无序,意味着系统结构和运动的不确定和无规则:反之,,熵越小,系统越有序,意味着具有确定和有 ...
随机推荐
- Day04_NTFS安全权限&文件共享服务器
NTFS安全权限 一.NTFS权限概述 1.通过设置NTFS权限,实现不同的用户访问同一个对象但是具有不同的访问权限 2.分配了正确的访问权限后,用户才能访问其资源 3.设置权限防止资源被篡改.删除 ...
- mongoose子文档生成不了_id,查询困难的解决办法
以下是我的数据库表 本来是想设置一个自增属性,比如listId,来定义我的子list,sliderlist这些,这样能确保他的唯一性,结果尝试了很久都无法成功,原生,插件都无法成功, 这两个网址是讲的 ...
- PHP fnmatch() 函数
定义和用法 fnmatch() 函数根据指定的模式来匹配文件名或字符串. 语法 fnmatch(pattern,string,flags) 参数 描述 pattern 必需.规定要检索的模式. str ...
- PHP floatval()、doubleval () 函数
floatval 函数用于获取变量的浮点值. floatval 不能用于数组或对象.高佣联盟 www.cgewang.com 版本要求:PHP 4 >= 4.2.0, PHP 5, PHP 7. ...
- PHP strcoll() 函数
实例 比较字符串: <?php高佣联盟 www.cgewang.comsetlocale (LC_COLLATE, 'NL');echo strcoll("Hello World!&q ...
- luogu P5325 Min_25筛
LINK:Min_25筛 新版感觉有点鬼畜 而且旧版的也够用了至少. 这个并不算很简单也不算很困难的知识点 学起来还是很麻烦的. (误入了很多dalao的blog 说的云里雾里的 甚是懵逼 这里推荐几 ...
- 牛客练习赛63 C 牛牛的揠苗助长 主席树 二分 中位数
LINK:牛牛的揠苗助长 题目很水 不过做法很多 想到一个近乎O(n)的做法 不过感觉假了 最后决定莽一个主席树 当然 平衡树也行. 容易想到 答案为ans天 那么一些点的有效增长项数为 ans%n. ...
- 使用ProxySQL实现MySQL Group Replication的故障转移、读写分离(一)
导读: 在之前,我们搭建了MySQL组复制集群环境,MySQL组复制集群环境解决了MySQL集群内部的自动故障转移,但是,组复制并没有解决外部业务的故障转移.举个例子,在A.B.C 3台机器上搭建了组 ...
- day18.os模块 对系统进行操作
一.os操作 1.system()在python中执行系统命令 # os.system("ifconfig") # os.system("touch 1.txt" ...
- maven中的陌生单词
有个单词记不住啊: artifact:人工制品,手工艺品,加工品; 石器; 词根:fac,fact,fect,fic,fig=make,do,表示“做,制作” 因此 art i fact 意思很好 ...