N皇后求解。万万没想到，只用一个一维数组就搞定了。还体现了回溯。

一、啥是N皇后？先从四皇后入手

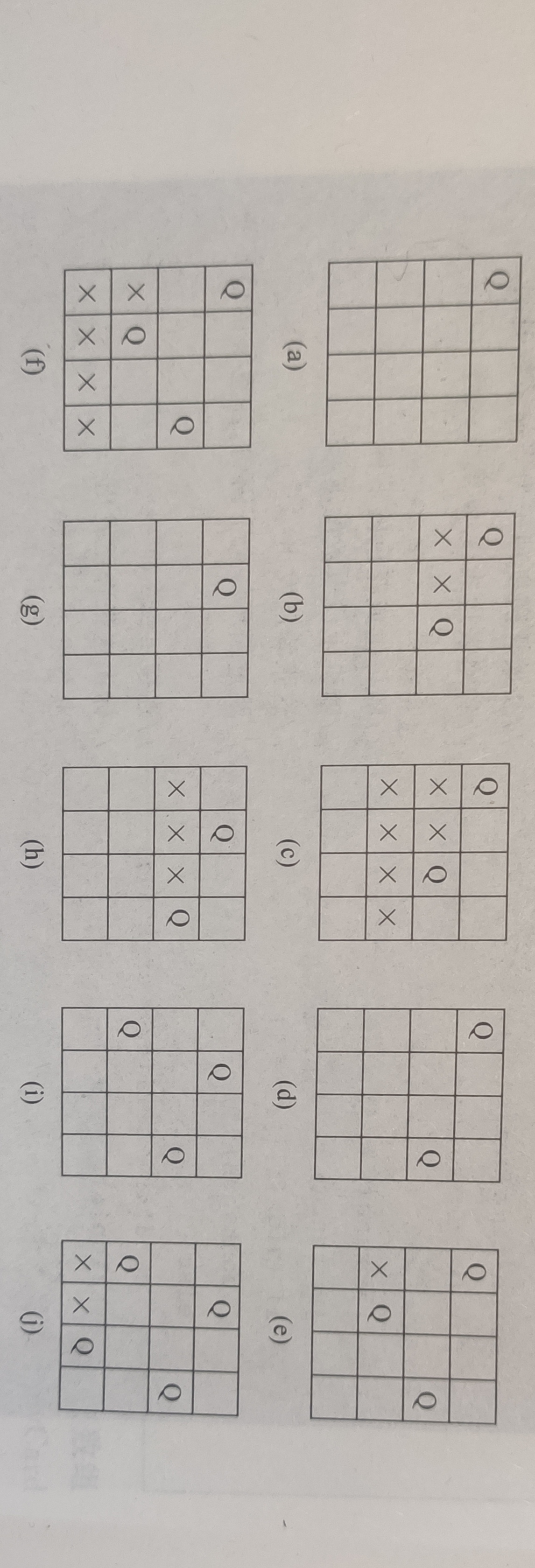
给定一个4x4的棋盘，要在棋盘上放置4个皇后。他们的位置有这样的要求，每一列，每一行，每一对角线都能有一个皇后。

你可能会对这个对角线有疑惑，其实就是每一个小正方形的对角线都不能有皇后。可以看图理解一下。

---

二、解题思想

设皇后k摆放在x[k]的位置上，注意数组下标从0开始，0<=k<n且0<=x[k]<n。

这里用数组下标以及对应的值，模拟了一个棋盘的行和列。这是比较奇妙的地方，不需要二维数组了。

算法:setQueen(n)

输入:皇后的个数n

输出:n皇后问题的解x[n]。解是一个数组。

1. 初始化 k=0 初始化解向量 x[n] ={-1}
2. 重复执行下面操作，摆放皇后k
   
   2.1. 把皇后k摆放在下一列的位置，即 x[k]++
   
   2.2. 如果皇后k摆放在x[k]位置发生冲突，则 x[k]++ 试探下一列，直到不冲突或 x[k] 出界
   
   2.3. 如果 x[k] 没出界并且所有皇后都摆放完毕，则输出一个解
   
   2.4. 如果 x[k] 没出界但有皇后尚未摆放，则 k++ ，转2.1摆放下一行的皇后
   
   2.5. 如果 x[k] 出界，则回溯，x[k]=-1 , k-- ,转2.1重新摆放上一行皇后

三、代码实现

#include <stdio.h>
#include <cstring>
#include <math.h>
class Queen
{
private:
    int Place(int k);
    int *x;
    int num;

public:
    Queen(int n);
    void setQueen();
    void PrintQueen();
    ~Queen();
};

Queen::Queen(int n)
{
    x = new int[n];
    memset(x, -1, n); //-1表示尚未摆放皇后
    num = n;
}

Queen::~Queen()
{
    delete[] x;
}

void Queen::setQueen()
{
    int k = 0, count = 0;
    while (k >= 0) //摆放皇后k，注意0<=k<n
    {
        x[k]++;                             //在下一列摆放皇后k
        while (x[k] < num && Place(k) == 1) //发生冲突
            x[k]++;                         //皇后k试探下一列，超出num将会跳出
        if (x[k] < num && k == num - 1)     //得到一个解
        {
            printf("第%d个解:", ++count);
            PrintQueen();
        }
        else if (x[k] < num && k < num - 1) //尚有皇后未摆放
            k = k + 1;                      //准备摆放下一个皇后
        else
            x[k--] = -1; //重置x[k],回溯，重新摆放皇后k
    }
}

//放置皇后。在一个位置上放置皇后，然后将结果返回。
int Queen::Place(int k) //考察皇后k放置在x[k]列是否发生冲突
{
    for (int i = 0; i < k; i++)
        if (x[i] == x[k] || abs(i - k) == abs(x[i] - x[k])) //根据对角线原则
            return 1;                                       //冲突返回1
    return 0;                                               //不冲突返回0
}

//打印皇后的解
void Queen::PrintQueen()
{
    for (int i = 0; i < num; i++)
        printf("%d\t", x[i] + 1);
    printf("\n");
}

int main(void)
{
    int n;
    printf("请输入皇后个数(n>=4):");
    scanf("%d", &n);
    Queen Q(n);
    Q.setQueen();
    return 0;
}

四、总结

这里面的代码是来自「数据结构C++王红梅版」

也知道了很多新颖的点

1. 代码中就很好利用了数组下标作为形象上理解的一行
2. 如何判定两个皇后是不是在同一对角线。也很好地利用了正方形的特性，皇后所在位置的行差与列差是否相等。
3. 还有就是SetQueen()的逻辑结构，先用while循环摆放皇后，然后根据这个结果来判断是已经求解到了，还是该下一行或者回溯到上一行。

这里放一波我之前逻辑结构很混乱的代码(就可以求解到正确答案，但是输出的时机很难控制)

#include <stdio.h>
#include <string.h>
#include <math.h>
#define n 4 //设定n皇后的数目
int *x = new int[n];

void printA();
int place(int k);
int main(void)
{

    memset(x, -1, sizeof(int) * n);
    int k = 0;
    while (k > -1)
    {
        x[k]++;
        if (k < n && place(k) == 1) //不冲突,开始放置下一行   如果已经是最后一行呢？
        {
            if (k < n - 1)
                k++;
        }
        else if (k < n || x[k] == n) //要回溯到上一行
        {
            x[k] = -1;
            k--;
        }
        else if (k == n && x[k] < n)
        {
            //得到一组解答
            printA();
        }
    }

    return 0;
}

//在第k行放置皇后，返回1代表冲突，返回0代表不冲突
int place(int k)
{
    for (; x[k] < n; x[k]++)
    {
        bool flag = true;
        for (int i = 0; i < k; i++)
        {
            if (x[k] == x[i] || (abs(k - i) == abs(x[k] - x[i])))
            {
                flag = false;
                break;
            }
        }
        if (flag)
            return 1;
    }
    return 0;
}

void printA()
{
    for (int i = 0; i < n; i++)
    {
        printf("%d  ", x[i] + 1);
    }
    printf("\n");
}