hdu2333-贪心，如何去后效性，背包太大怎么办，如何最大化最小值，从无序序列中发掘有序性质

补充一下我理解的中文题意。。

你要重新组装电脑。。电脑有一些部件。。
你的预算有b，b(1~1e9),有n个部件。。
每个部件有类型和名称以及价钱和质量
现在你要在不超过预算b的情况下。。
每个类型都买一个部件。。然后最终的质量由最小的质量决定
在此约束下问你在预算b之内能组装的最大的质量是多少
对每个部件价钱范围1e6,质量范围1e9

===============

由于钱和质量没有必然联系

所以我们不能直接从质量小的开始贪。。

也没法从质量大的开始贪吧。。因为你还要保证你的钱要够

按质量排序则钱是无序的。。这样反正不好处理。。其他的处理方法我还没有想到

所以说你要怎么搞呢。。

a1,b1,a2,b2,a3,b3

c1,d1,c2,d2,c3,d3

x1,y1,x2,y2,x3,y3

因为一旦你的钱固定的话。。对于每一个枚举的总钱数。。这里的钱数是固定的。。

也就是dp中离散的钱数。。每一个枚举的钱数状态来说。。钱是固定的。。

所以你第一种取不取。。会对后面造成影响。。因为总钱数少了。。

好像也不是太好dp,如果算前i种物品剩余钱数是j所能达到的最大的最小质量

我后来想算前i种物品能够达到质量q的最小钱数。。但是由于q很大不能离散。。所以不能dp?这个理由好像很牵强。。

我现在也不是太清楚离散化和dp之间是什么关系。。但是毫无疑问对于一些连续的问题dp解决不了

一种解法是说。。我们二分最后的质量q。。

之前我在纠结

如果大于等于q1的最便宜的所有零件的组合超过预算。。

大于等于q2(q2>q1)的最便宜的所有零件的组合却不超过预算
但是这是不存在的。。q单调增加时。。最便宜的价格也单调递增。。

 价格虽然无序。。但随着有序性质质量的单调递增。。最小价格单调递增。。
我大概是表达这个意思。。 

因为如果质量小，这意味着你的选择性更多（比质量大的），所以也就最小价格也就可能越小

所以我们来二分一下最小质量。。因为每次都取最便宜的部件。。所以说。。其总价格也是单调递增的，前面证过了。。

所以对于每次二分的结果。。对每种部件取大于等于这个结果的最便宜的部件。。最后check超不超过预算

超过就质量往左走。。不超过就往右走。。，最后就能求出大于等于q的最小预算 ，最后就能求出来大于等于q的最小预算在不超过总预算的

情况下所能达到的最大的q

 

 

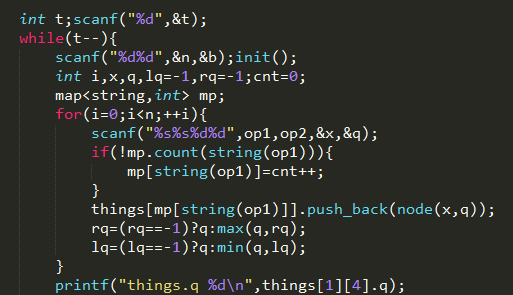
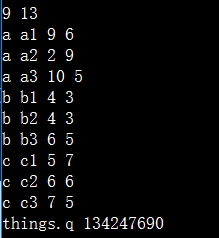
按理说我的下标只能到2..因为一共3个元素。。

但是。。下标3,4却能访问。。不报越界。。其值是一个野值吧。。

这一点我们以后一定要注意。。

但是你如果程序一开始你就访问4.。就会停止运行。。

这个vector的trick一定要记好了。。

#include <iostream>
#include <cstdio>
#include <map>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
int n,b,cnt;
char op1[50];char op2[50];
struct node{int x,q;node(int x,int q):x(x),q(q){}};
typedef long long ll;
const int maxn=1e3+7;
vector<node> things[maxn];
int mxcheap[maxn][maxn];
bool cmp(node a,node b){return (a.q!=b.q)?a.q<b.q:a.x<b.x;}
void init(){int i;for(i=0;i<maxn;++i) things[i].clear();}
void Sort(){int i;for(i=0;i<cnt;++i) sort(things[i].begin(),things[i].end(),cmp);}
bool check(int key){int i;ll sum=0;
    for(i=0;i<cnt;++i){
        int left=0,right=things[i].size()-1,mid;
        while(left<=right){
            mid=(left+right)>>1;
            if(things[i][mid].q<key) left=mid+1;else right=mid-1;
        }
        if(right+1<things[i].size()&&things[i][right+1].q>=key) right++;
        if(left>things[i].size()-1) {
        return false;}
        sum+=mxcheap[i][right];
    }
    return (sum>b)?false:true;}
int main(){

    int t;scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&b);init();
        int i,j,x,q,lq=-1,rq=-1;cnt=0;
        map<string,int> mp;
        for(i=0;i<n;++i){
            scanf("%s%s%d%d",op1,op2,&x,&q);
            if(!mp.count(string(op1))){
                mp[string(op1)]=cnt++;
            }
            things[mp[string(op1)]].push_back(node(x,q));
            rq=(rq==-1)?q:max(q,rq);
            lq=(lq==-1)?q:min(q,lq);
        }
        Sort();
        for(i=0;i<cnt;++i){
            mxcheap[i][things[i].size()-1]=things[i].back().x;
            for(j=things[i].size()-2;j>=0;--j){
                mxcheap[i][j]=min(things[i][j].x,mxcheap[i][j+1]);
            }
        }
        int left=lq,right=rq,mid,ans=-1;
        while(left<=right){
            mid=(left+right)>>1;
            if(check(mid)){left=mid+1;}
            else{right=mid-1;}
        }
        if(check(right+1)) right++;
        printf("%d\n",right);
    }
    return 0;
}

这里我犯了一个错。。那就是。。check中的二分写错了。。

即使写对了也不对。。因为。。我以为质量最接近q的价格最便宜。。这只是对所有等于q的东西来说。。

那么对于大于q的可能更加便宜。。所以我们这里需要预处理出每种部件的i~size的区间的最小值。。

二分得到边界即可。。但是对于二分来讲。。我们应当既考虑left>size-1(size是vector的size)

也要考虑left<0,比如要求第一个》=q的元素的下标。。这里如果全部大于key那么right会小于0，

你要判断right+1合不合法以免漏判，如果全部小于key那么right=size-1,而left=size,此时left

就越界了。。这是妥妥的无解。。一定要注意这一点

性质：任何无序序列的区间i~n的最值都是单调的