[IOI1998] Polygon (区间dp，和石子合并很相似)

题意：

给你一个多边形（可以看作n个顶点，n-1条边的图），每一条边上有一个符号（+号或者*号），这个多边形有n个顶点，每一个顶点有一个值

最初你可以把一条边删除掉，这个时候这就是一个n个顶点，n-2条边的图

如果顶点i和j之间有边，那么你可以把i点和j点合并成一个点，把这个点替换掉i、j两个点，这个新点的值是i+j 或者 i*j （这个是要看连接i和j两点的边上的符号）

经过若干次操作之后剩下一个点，这个点的值最大是多少

题解：

这道题目和石子合并题目很相似，这里先说一下石子合并

题目：

有N堆石子围成一个圆，现要将石子有序的合并成一堆，规定如下：每次只能移动相邻的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

我们来分析一下，给你 4 堆石子：4,5,6,7，按照下图所示合并

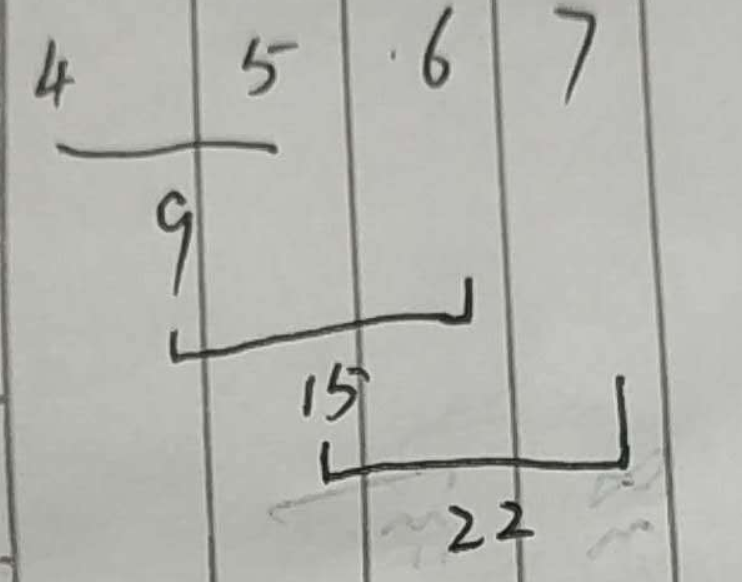
这种合并方式的花费为：4+5+9+6+15+7=46

这种合并也就是4->5->6->7按照这个方向进行

那我们先合并前3堆石子：4+5+9+6

这个花费就是：第一堆和第二堆合并的花费+第一堆和第二堆合并之后的数量+第三堆的数量

那我们先合并前4堆石子：4+5+9+6+15+7

这个花费就是：第一堆和第二堆和第三堆合并的花费（也就是4+5+9+6）+第一堆和第二堆和第三堆合并之后的数量+第四堆的数量

大问题分解成了小问题，而且大问题包含了小问题的解，大问题和小问题同质同解。完完全全满足dp的性质。

剩下的就是从中找到最优解，因为当前是从1->2->3->4的顺序去合并的，还有(1->2)->(3->4)或者1->(2->3->4)的顺序，原理一样，这里面因为第二第三部分是固定的，所以只需要得到小问题的最优解，就可以求得大问题的最优解了。这一点我们可以把原序列复制一份追加到原序列尾部，然后使用区间dp枚举就可以了

这里给出石子合并问题求最大花费的代码：dp[i][j]表示：从石子i合并到石子j所能得到的最大花费

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxn=450;//区间长度为2*n
 4 int dp[maxn][maxn];
 5 int sum[maxn];//前缀和数组
 6 int a[maxn];//每堆石子的个数
 7 int main()
 8 {
 9     int n,x;
10     sum[0]=0;
11     while(scanf("%d",&n)!=EOF){
12         memset(dp,0,sizeof(dp));
13         memset(sum,0,sizeof(sum));
14         for(int i=1;i<=n;i++){
15             scanf("%d",&a[i]);
16             sum[i]=sum[i-1]+a[i];//预处理
17             dp[i][i]=0;
18         }
19
20         int in=1;//首尾相连之后
21         for(int i=n+1;i<=2*n;i++)
22             sum[i]+=(sum[i-1]+a[in++]);
23
24         for(int len=2;len<=n;len++)//枚举区间长度
25         {
26             for(int i=1;i<=2*n;i++)//枚举区间起点
27             {
28                 int j=i+len-1;//区间终点
29                 if(j>n*2) break;//越界结束
30                 for(int k=i;k<j;k++)//枚举分割点，构造状态转移方程
31                 {
32                     dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+(sum[j]-sum[i-1]));
33                 }
34             }
35         }
36         int MAX=-1;
37         for(int i=1;i<=n;i++)//枚举环状序列的起点，长度为n
38         MAX=max(dp[i][i+n-1],MAX);//求最大值
39         printf("%d\n",MAX);
40     }
41     return 0;
42 }

回归原题，这个题目如果所有边的符号都是+号，那就和石子合并一样了

这里多了一个*号，那么两个很小的负数相乘也可以得到一个很大的值，这样的话，我们可以开一个三维dp，dp[i][j][k]：如果k==1，那就保存的是dp[i][j]的max

如果k==0，那就保存dp[i][j]的最小值

其他和正常区间dp一样

代码：

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<iostream>
using namespace std;
#define mem(a) memset(a,0,sizeof(a))
typedef long long ll;
const int maxn=55;
const int INF=0x3f3f3f3f;
const double blo=(1.0+sqrt(5.0))/2.0;
const double eps=1e-8;
struct shudui
{
    int a,b;
}que[maxn];
int dp[maxn][maxn][2],num[maxn],str[maxn];
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        char s[maxn];
        for(int i=1;i<=2*n;++i)
        {
            if(i%2)
            {
                scanf("%s",s);
                str[i/2]=s[0];
            }
            else
            {
                scanf("%d",&num[(i-1)/2]);
            }
        }
        str[n]=str[0];
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<n;++j)
            {
                if(i==j)
                    dp[i][j][0]=dp[i][j][1]=num[i];
                else
                {
                    dp[i][j][0]=INF;
                    dp[i][j][1]=-INF;
                }
            }
        }
        for(int len=1;len<n;++len)
        {
            for(int i=0;i<n;++i)
            {
                //int j=(i+len)%n;
                int j=(i+len);
                for(int k=i;k<j;++k)
                {
                    if(str[(k+1)%n]=='t')
                    {
                        dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][1]+dp[(k+1)%n][j%n][1]);
                        dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]+dp[(k+1)%n][j%n][0]);
                    }
                    else
                    {
                        dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][1]*dp[(k+1)%n][j%n][1]);
                        dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][0]*dp[(k+1)%n][j%n][0]);
                        dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]*dp[(k+1)%n][j%n][1]);
                        dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][1]*dp[(k+1)%n][j%n][0]);
                        dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]*dp[(k+1)%n][j%n][0]);
                    }
                }
            }
        }
        //printf("%d %d %d %d\n",dp[1][2][1],dp[2][1][1],dp[2][3][1],dp[3][2][1]);
        int maxx=-INF,index=0;
        for(int i=0;i<n;++i)
        {
            maxx=max(maxx,dp[i][(i+n-1)%n][1]);
        }
        for(int i=0;i<n;++i)
        {
            if(dp[i][(i+n-1)%n][1]==maxx)
            {
                //printf("%d %d\n",i,(i+n-1)%n);
                que[index++].a=i+1;
                //que[index++].b=max((i+n-1)%n,i)+1;
                //que[index++].a=i+1;
            }
        }
        printf("%d\n",maxx);
        for(int i=0;i<index;++i)
        {
            //printf("%d %d\n",que[i].a,que[i].b);
            if(i==index-1)
            printf("%d\n",que[i].a);
            else printf("%d ",que[i].a);
        }
    }
    return 0;
}