canvas基础[二]教你编写贝塞尔曲线工具

贝塞尔曲线

bezierCurveTo

在线工具

https://canvature.appspot.com/ [感觉这个好用一些]

https://blogs.sitepointstatic.com/examples/tech/canvas-curves/bezier-curve.html

三次贝塞尔曲线必须包含三个点。前两个点（cp1x，cp1y）和（cp2x，cp2y）是在三次贝塞尔曲线计算中使用的控制点，最后一个点（x，y）是曲线的终点。

bezierCurveTo（cp1x，cp1y，cp2x，cp2y，x，y）

参量	类型	描述
cp1x	number	第一个贝塞尔控制点的x坐标。
cp1y	number	第一个贝塞尔控制点的y坐标。
cp2x	number	第二个贝塞尔控制点的x坐标。
cp2y	number	第二个贝塞尔控制点的y坐标。
X	number	要添加到当前路径的点的x坐标。
y	number	要添加到当前路径的点的y坐标。

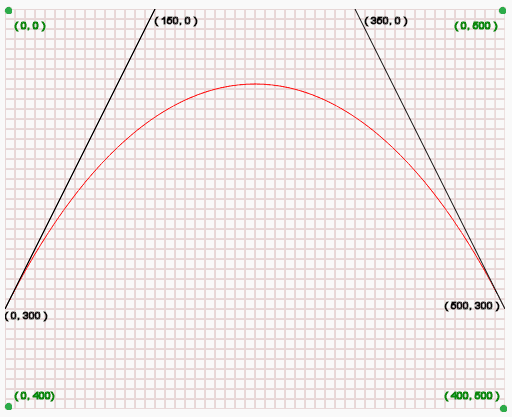
• （0，300）是曲线的起点。[这个用moveTo(x,y)叹气的点]

• （150，0）即（cp1x，cp1y）是曲线的第一个控制位置。

• （350，0）即（cp2x，cp2y）是曲线的第二个控制位置。

• （500，300），即（x，y）是曲线的终点。

quadraticCurveTo

二次贝塞尔曲线,需要两个点,控制点和曲线的终点

• （0，300）是曲线的起点。
• （250，0）即（cp1x，cp1y）是曲线的控制位置。
• （500，300），即（x，y）是曲线的终点。

绘制可视化的二次贝塞尔曲线demo

初始化

<style>
    * {
      margin: 0;
      padding: 0;
    }

    #app {
      width: 100vw;
      height: 100vh;
      min-width: 1100px;
      overflow: hidden;
      font-family: 'Lato', sans-serif;
      background-color: #ffffff;
    }

    #canvas {
      border: 1px solid #ccc;
      position: absolute;
      top: 20px;
      left: 20px;
    }
    #code{
      margin-top:20px;
      margin-left:520px;
      display: inline-block;
      padding: 0.5em;
      background: #002b36;
      color: #839496;
      min-height: 11rem;
      font-family: Consolas;
      font-size: 20px;
    }
  </style>
<div id="app">
  <canvas id="canvas" width="500" height="500"></canvas>
  <pre id="code">code</pre>
</div>

  let canvas = document.querySelector('#canvas')
  // 代码文本
  let code = document.querySelector('#code');
  let ctx = canvas.getContext('2d'),
    point,
    style = {// 原点样式
      radius: 10,
      width: 2,
      color: '#900',
      fill: 'rgba(200,200,200,.5)',
      arc1: 0,
      arc2: 2 * Math.PI
    },
    drag = null,// 按下的时候 确认鼠标拿的那一个点
    dPoint, // 拿到当前点的坐标
    cpline = {
      width: 1,
      color: 'red'
    },
    curve = {
      width: 6,
      color: '#333'
    }
   // 初始化默认数据
  function init() {
    point = {// 鼠标的三个点
      p1: {  // moveTo
        x: 100, y: 50
      },
      cp1: { // 贝塞尔第一个点
        x: 100, y: 200
      },
      p2: {// 贝塞尔第二个点
        x: 300, y: 200
      }
    }
  }
  // 代码文字
  function showCode() {
    if (code) {
      code.firstChild.nodeValue =
        "theCanvas = document.getElementById(\"canvas\");\n" +
        "ctx = theCanvas.getContext(\"2d\")\n" +
        "ctx.lineWidth = " + curve.width +
        ";\nctx.strokeStyle = \"" + curve.color +
        "\";\nctx.beginPath();\n" +
        "ctx.moveTo(" + point.p1.x + ", " + point.p1.y + ");\n" +
        "ctx.quadraticCurveTo(" + point.cp1.x + ", " + point.cp1.y + ", " + point.p2.x + ", " + point.p2.y + ");"
        +
        "\nctx.stroke();"
      ;
    }
  }

画出页面

  function drawScreen() {
    // 清空画布
    ctx.clearRect(0, 0, canvas.width, canvas.height)
    ctx.lineCap = 'round';
    ctx.lineJoin = 'round';
    ctx.lineWidth = cpline.width;
    ctx.strokeStyle = cpline.color;
    ctx.beginPath()
    ctx.moveTo(point.p1.x, point.p1.y)
    ctx.lineTo(point.cp1.x, point.cp1.y)
    ctx.lineTo(point.p2.x, point.p2.y)
    ctx.stroke();
    //中间的弧度
    ctx.lineWidth = curve.width;
    ctx.strokeStyle = curve.color;
    ctx.beginPath();
    ctx.moveTo(point.p1.x, point.p1.y)
    ctx.quadraticCurveTo(point.cp1.x, point.cp1.y, point.p2.x, point.p2.y)
    ctx.stroke();
    // 三个原点
    for (let p in point) {
      console.log(p);
      ctx.lineWidth = style.width;
      ctx.strokeStyle = style.color;
      ctx.fillStyle = style.fill;
      ctx.beginPath();
      ctx.arc(point[p].x, point[p].y, style.radius, style.arc1, style.arc2, true)
      ctx.fill();
      ctx.stroke();
    }
    showCode()
  }

拿到鼠标的鼠标

  // 鼠标的坐标
  function MousePos(event) {
    event = event ? event : window.event;
    return {
      x: event.pageX - canvas.offsetLeft,
      y: event.pageY - canvas.offsetTop
    }
  }

问个来了,当我们鼠标移动的时候怎么确定鼠标放在圆里面啦

这里又运用了初中数学知识圆的标准方程

 canvas.addEventListener('mousedown', dragStart, false);
 canvas.addEventListener('mousemove', dragging, false);
 canvas.addEventListener('mouseup', dragEnd, false);
 canvas.addEventListener('mouseout', dragEnd, false);

这里我们需要知道点应该在圆内

  鼠标按下的时候
function dragStart(e) {
    e = MousePos(e)
    let dx, dy;
    // 找到鼠标拿到哪一个点
    for (let p in point) {
      dx = point[p].x - e.x;
      dy = point[p].y - e.y;
      if ((dx ** 2) + (dy ** 2) < style.radius ** 2) {
          // 确定了拿到那个点
        	drag = p;
          // 确定了拿到点的鼠标
          dPoint=e;
        canvas.style.cursor = 'move';
        return;
      }
    }
  }

鼠标移动

 function dragging(e) {
    // 这个是用来判断有按下的参数的时候触发
    if (drag) {
      e = MousePos(e);
        // 鼠标的x - 开始鼠标的点
      point[drag].x += e.x - dPoint.x;
      point[drag].y += e.y - dPoint.y;
      dPoint = e;
      drawScreen();
    }
  }

鼠标离开

function dragEnd(e) {
    drag = null;
    canvas.style.cursor = 'default';
    drawScreen();
  }

See the Pen Canvas: Quadratic Curve 二次曲线 by 973782523
(@973782523) on CodePen.

再二次贝塞尔曲线的基础上绘制三次贝塞尔曲线

修改1,给html添加一个class

  <canvas id="canvasOne" width="500" height="500" class="bezier"></canvas>

在初始化数据的时候,添加第二个点

 // 初始化默认数据,默认不传参数三次贝塞尔曲线,不默认二次
  function init(quadratic) {
     ....
   if (quadratic) {
      point.cp1={
        x:250,y:100
      }
    }else{
      point.cp1={
        x:150,y:100
      }
      point.cp2={
        x:350,y:100
      }

  }

画出屏幕的时候

function drawScreen() {
...
ctx.lineTo(point.cp1.x, point.cp1.y)
// 判断是否有第二个点
    if (point.cp2) {
      ctx.moveTo(point.p2.x,point.p2.y)
      ctx.lineTo(point.cp2.x,point.cp2.y)
    }else{
      ctx.lineTo(point.p2.x, point.p2.y);
    }
...
	ctx.moveTo(point.p1.x, point.p1.y)
    // 确认二次还是三次
    if (point.cp2) {
      ctx.bezierCurveTo(point.cp1.x, point.cp1.y, point.cp2.x, point.cp2.y, point.p2.x, point.p2.y)
    }else{
      ctx.quadraticCurveTo(point.cp1.x, point.cp1.y, point.p2.x, point.p2.y);
    }
...
}

修改代码显示的部分

 +(point.cp2 ?
						"ctx.bezierCurveTo("+point.cp1.x+", "+point.cp1.y+", "+point.cp2.x+", "+point.cp2.y+", "+point.p2.x+", "+point.p2.y+");" :
						"ctx.quadraticCurveTo("+point.cp1.x+", "+point.cp1.y+", "+point.p2.x+", "+point.p2.y+");"
					) +

See the Pen Canvas: Bezier Curve by 973782523
(@973782523) on CodePen.