7.1 NOI模拟赛 计数问题 dp

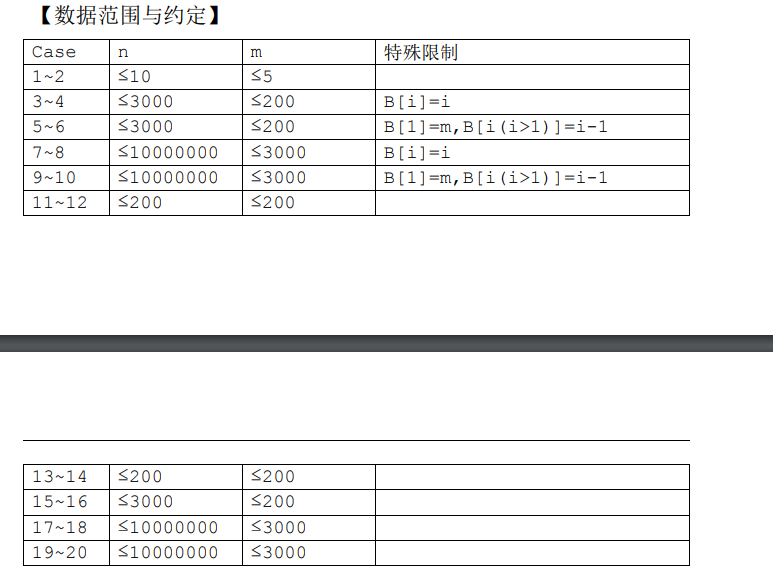
还是可以想出来的题目 不过考场上没有想出来 要 引以为戒。

初看觉得有点不可做 10分给到了爆搜。

考虑第一个特殊情况 B排列为1~m.

容易发现A排列中前m个数字 他们之间不能产生交换 且 第k个数字要交换到后面的m+1~n这些数字的时候 k~m的数字都要进行交换才行。

那么直接枚举有多少个数字到后面了 组合数可以解决 考虑剩下的那些空位怎么办。

其实就是要求出 \(f_i\) 其表示满足题目条件的i个数的排列的个数.

考虑递推 容易发现\(f_0=1,f_1=1\) 对于\(f_i\)考虑第i个数字不换 那么为\(f_{i-1}\)换的话有i-1种方法 对应的方案为\((i-1)\cdot f_{i-2}\)

综上可以得到\(f_i=f_{i-1}+(i-1)\cdot f_{i-2}\)

这样结合上面的dfs就可以获得30分了。

考虑另外一种递推的模型 可以发现m在第一个 那么就要想办法将m换到第一个。

显然 m可以不动 那么剩下的m-1个数字就要放到后面了。

m可以直接和1交换 那么剩下的m-2个数字要放到后面。

m还可以和后面的进行交换 其实就是m个数字放到后面。

三种情况分别讨论即可。结合上面的两种方法就可以得到50分了。具体细节看代码。

上午也只推到这里。因为感觉正解比较难 所以就每有一直探索下去 其实可以继续走下去。

考虑正解：综上其实可以发现 m个数全部扔到后面是一定合法的，那么其实就是考虑有多少个数字可以被扔到前面。

如果有k个数字在后面 那么前面这s=m-k个数字就应该在前面 且他们不能和后面的k个数字存在交换。

这样就要求他们是一个合法排列 容易想到合法情况最多只有一种 这点容易证明。

也就是说此时只需要判断s个数字放到前面是否合法 即满足题目中的条件。

可以暴力安排位置 因为第一个要放到数值最小的位置上去 这样暴力放然后再check即可。

复杂度\(m^2+n\)

code

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 100000000000000000ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-8
#define sq sqrt
#define mod 1000000007
#define S second
#define F first
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=30010,maxn=10000010;
int n,m,ans;
int a[MAXN],b[MAXN];
int vis[MAXN],f[maxn],fac[maxn],inv[maxn];
inline int ksm(int b,int p)
{
	int cnt=1;
	while(p)
	{
		if(p&1)cnt=(ll)cnt*b%mod;
		b=(ll)b*b%mod;p=p>>1;
	}
	return cnt;
}
inline void dfs(int x)
{
	if(x==n+1)
	{
		int cnt=1;
		rep(1,n,i){if(a[a[i]]!=i)return;if(a[i]==b[cnt])++cnt;}
		if(cnt>m)
		{
			++ans;
			//rep(1,n,i)cout<<a[i]<<' ';
			//cout<<endl;
		}
		return;
	}
	rep(1,n,i)
	{
		if(vis[i])continue;
		a[x]=i;vis[i]=1;
		dfs(x+1);
		vis[i]=0;
	}
}
inline int C(int a,int b){return (ll)fac[a]*inv[b]%mod*inv[a-b]%mod;}
inline int check()
{
	rep(2,m,i)if(b[i]!=i-1)return 0;
	return 1;
}
inline void prepare()
{
	f[0]=1;fac[0]=1;
	rep(1,n,i)
	{
		fac[i]=(ll)fac[i-1]*i%mod;
		f[i]=(f[i-1]+(ll)f[i-2]*(i-1))%mod;
	}
	inv[n]=ksm(fac[n],mod-2);
	fep(n-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
}
int main()
{
	freopen("1.in","r",stdin);
	//freopen("ya.out","w",stdout);
	get(n);get(m);int flag=0;
	if(n<m){put(0);return 0;}
	rep(1,m,i)
	{
		get(b[i]);
		if(b[i]!=i)flag=1;
	}
	if(n<=10)
	{
		dfs(1);put(ans);
		return 0;
	}
	prepare();
	if(m==1){put(f[n]);return 0;}
	if(n==m)
	{
		rep(1,m,i)if(b[b[i]]!=i){put(0);return 0;}
		put(1);return 0;
	}
	if(!flag)
	{
		int ww=min(m,n-m);
		rep(0,ww,i)ans=(ans+(ll)C(n-m,i)*f[n-m-i])%mod;
		put(ans);return 0;
	}
	if(b[1]==m&&check())
	{
		if(n>=2*m-2)//和1交换.
			ans=(ll)f[n-2*m+2]*C(n-m,m-2)%mod;
		if(n>=2*m-1)//不动.
			ans=(ans+(ll)f[n-2*m+1]*C(n-m,m-1))%mod;
		if(n>=2*m)//交换.
			ans=(ans+(ll)f[n-2*m]*C(n-m,m))%mod;
		put(ans);
	}
	else
	{
		if(n>=2*m)ans=(ans+(ll)f[n-2*m]*C(n-m,m))%mod;
		rep(1,m,i)//枚举前m个位置
		{
			if(n<2*m-i)continue;
			int flag=0,ww=0;
			vis[b[i]]=1;
			rep(1,i,j)
			{
				++ww;
				while(!vis[ww])++ww;
				a[b[j]]=ww;
			}
			rep(1,m,j)if(vis[j]&&a[a[j]]!=j){flag=1;break;}
			if(!flag)ans=(ans+(ll)f[n-2*m+i]*C(n-m,m-i))%mod;
			//cout<<flag<<endl;
		}
		put(ans);
	}
	return 0;
}