免费馅饼——移动dp

免费馅饼

题目描述

SERKOI最新推出了一种叫做“免费馅饼”的游戏:

游戏在一个舞台上进行。舞台的宽度为 \(W\) 格，天幕的高度为 \(H\) 格，游戏者占一格。

开始时游戏者站在舞台的正中央，手里拿着一个托盘。下图为天幕的高度为 \(4\) 格时某一个时刻游戏者接馅饼的情景。

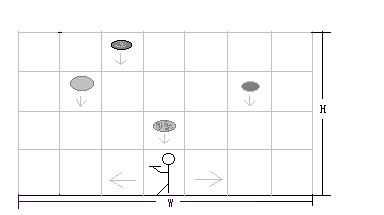
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。

馅饼有很多种，游戏者事先根据自己的口味，对各种馅饼依次打了分。同时，在 \(3-308\) 电脑的遥控下，各种馅饼下落的速度也是不一样的，下落速度以格/秒为单位。

当馅饼在某一秒末恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。

写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。

输入格式

输入文件的第一行是用空格隔开的两个正整数，分别给出了舞台的宽度 \(W\) （ \(1\) 到 \(99\) 之间的奇数）和高度 \(H\) （ \(1\) 到 \(100\) 之间的整数）。

接下来依馅饼的初始下落时间顺序给出了所有馅饼的信息。每一行给出了一块馅饼的信息。由四个正整数组成，分别表示了馅饼的初始下落时刻（ \(0\) 到 \(1000\) 秒），水平位置、下落速度（ \(1\) 到 \(100\) ）以及分值。游戏开始时刻为 \(0\) 。从 \(1\) 开始自左向右依次对水平方向的每格编号。

输入文件中同一行相邻两项之间用一个或多个空格隔开。

输出格式

输出文件的第一行给出了一个正整数，表示你的程序所收集的最大分数之和。

样例

样例输入

3 3
0 1 2 5
0 2 1 3
1 2 1 3
1 3 1 4

样例输出

12

数据范围与提示

馅饼个数
\in [0,2500]

思路

移动 \(dp\) ，重在移动，但是两个物体都移动处理起来还是很麻烦的，所以定馅饼不动，让人动，去接馅饼。

但是要注意的是馅饼在第 \(i\) 秒到第 \(i+1\) 秒的降落过程中，不可被接到，相当于闪现，在过程中不可选中。

所以只有在高度能够被速度整除的时候，才可以被接到，所以有的馅饼可以除去，不考虑。

设 \(f[i][j]\) 为在第 \(i\) 时刻，小人在第 \(j\) 的坐标，能够接到的最大值。

用 \(k\) 枚举小人移动的距离 \((-2、-1、0、1、2)\) ，动态转移方程：

\(f[i][j]=min(f[i][j],f[i-1][j+k]+a[i][j])\)

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn=2500+50;
int w,h;
int dp[maxn][maxn];
int maxtime;
int dx[5]={0,1,-1,2,-2};
struct Node{
    int t0;
    int t1;
    int a0;
    int v;
    int w;
}e[maxn];
int Cala(int t,int now){
    int ans=0;
    for(int i=0;i<=5;i++){
        if(now+dx[i]<0||now+dx[i]>w)continue;//如果走出了横坐标的范围，直接跳过
        ans=max(ans,dp[t+1][now+dx[i]]);
    }
    return ans;
}

int main(){
    scanf("%d%d",&w,&h);
    h--;
    int tot=1;
    while(~scanf("%d%d%d%d",&e[tot].t0,&e[tot].a0,&e[tot].v,&e[tot].w)){
        if(h%e[tot].v==0){//只有在高度能够被速度整除的时候，才可以被接到
            e[tot].t1=e[tot].t0+h/e[tot].v;
            maxtime=max(maxtime,e[tot].t1);
            tot++;
        }
    }
    if(tot==1){//若没有馅饼可接，直接输出0
        printf("0\n");
        return 0;
    }
    if(w==1){//若宽度只有1，直接将全部求和
        int sum=0;
        for(int i=1;i<=tot;i++){
            if(e[i].a0==1){
                sum+=e[i].w;
            }
        }
        printf("%d\n",sum);
        return 0;
    }
    for(int i=1;i<=tot;i++){//初始化
        dp[e[i].t1][e[i].a0]+=e[i].w;
    }
    for(int i=maxtime-1;i>=0;i--){
        for(int j=w;j>=1;j--){
            dp[i][j]+=Cala(i,j);
        }
    }
    printf("%d\n",dp[0][w/2+1]);
    return 0;
}