蓝桥杯——快速排序（2018JavaB组第5题9分）

快速排序（18JavaB5,9’）

以下代码可以从数组a[]中找出第k小的元素。

它使用了类似快速排序中的分治算法，期望时间复杂度是O(N)的。

请仔细阅读分析源码，填写划线部分缺失的内容。

import java.util.Random;
public class Main{
	public static int quickSelect(int a[], int l, int r, int k) {
		Random rand = new Random();
		int p = rand.nextInt(r - l + 1) + l;
		int x = a[p];
		int tmp = a[p]; a[p] = a[r]; a[r] = tmp;
		int i = l, j = r;
		while(i < j) {
	while(i < j && a[i] < x) i++;
	if(i < j) {
	a[j] = a[i];
	j--;
	}
	while(i < j && a[j] > x) j--;
	if(i < j) {
	a[i] = a[j];
	i++;
	}
	}
	a[i] = x;
	p = i;
	if(i - l + 1 == k) return a[i];
	if(i - l + 1 < k) return quickSelect( _________________________________ ); //填空
	else return quickSelect(a, l, i - 1, k);
	}
	public static void main(String args[]) {
		int [] a = {1, 4, 2, 8, 5, 7};
		System.out.println(quickSelect(a, 0, 5, 4));
	}
}

注意：只提交划线部分缺少的代码，不要抄写任何已经存在的代码或符号。

---

先看看典型的快速排序

快速排序

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序

它采用了一种分治(Divide-and-ConquerMethod)的策略

基本思想

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

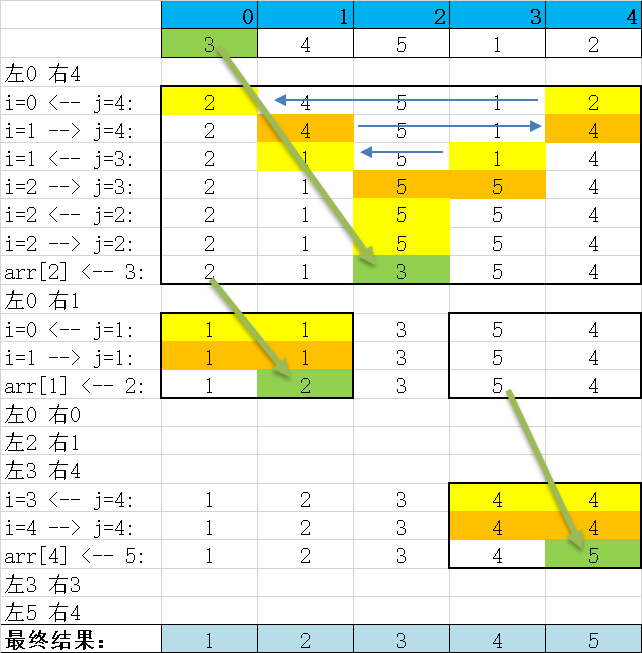
先把基准值（最左）存起来

高位（右）大的往左边拉

低位（左）小的往右边拉

最后，存的那个基准值（曾经最左）放中间

对左：相同处理

对右：相同处理

package bb;
public class QuickSortMy {
	static void printArray(int a[]) {
		for (int i : a) {
			System.out.print(i + "\t");
		}
		System.out.println();
	}
	static void qsort(int a[], int left, int right) {
		if (left >= right) {
			return;
		}
		printArray(a);
		int key = a[left];
		int i = left, j = right;
		while (i < j) {
			while (i < j && a[j] > key) {
				j--;
			}
			if (i < j) {
				System.out.printf("a[%d]=%d <- a[%d]=%d\n", i, a[i], j, a[j]);
				a[i++] = a[j];
			}
			while (i < j && a[i] < key) {
				i++;
			}
			if (i < j) {
				System.out.printf("a[%d]=%d -> a[%d]=%d\n", i, a[i], j, a[j]);
				a[j--] = a[i];
			}
		}
		a[i] = key;
		printArray(a);
		qsort(a, left, i - 1);
		qsort(a, i + 1, right);
	}
	public static void main(String[] args) {
		int a[] = { 3, 4, 5, 1, 2 };
		qsort(a, 0, a.length - 1);
	}
}

---

2018JavaB组第5题的参考答案+注释如下所示：

package bb;
import java.util.Random;
public class JB18_5快速排序 {
	public static int quickSelect(int a[], int l, int r, int k) {
		Random rand = new Random();
		int p = rand.nextInt(r - l + 1) + l;
		int x = a[p];
		int tmp = a[p];
		a[p] = a[r];
		a[r] = tmp;
		int i = l, j = r;
		while (i < j) {
			while (i < j && a[i] < x)
				i++;
			if (i < j) {
				a[j] = a[i];
				j--;
			}
			while (i < j && a[j] > x)
				j--;
			if (i < j) {
				a[i] = a[j];
				i++;
			}
		}
		a[i] = x;
		p = i;
		if (i - l + 1 == k)// (1)说明到底了
			return a[i];
		if (i - l + 1 < k)
			return quickSelect(a, i + 1, r, k - i + l - 1); // 填空
		// qsort(a, i + 1, right);
		// (3)先试试k，
		// (4)再考虑：k要移动到等于（i - l + 1），试试k-(i - l + 1)
		else
			// i - l + 1 > k
			return quickSelect(a, l, i - 1, k);// (2)qsort(a, left, i -
												// 1);对上了，k不变
	}
	public static void main(String args[]) {
		int[] a = { 1, 4, 2, 8, 5, 7 };
		System.out.println(quickSelect(a, 0, 5, 4));
		// int [] a = {1, 4, 2, 8, 5, 7, 23, 58, 16, 27, 55, 13, 26, 24, 12, 2};
		// System.out.println(quickSelect(a, 0, a.length-1, 6));
	}
}