差分进化算法介绍及matlab实现

引言

---

差分进化算法是基于群体智能理论的优化算法，是通过群体内个体间的合作与竞争而产生的智能优化搜索算法，它保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和“一对一”的竞争生存策略，降低了进化计算操作的复杂性。

差分进化算法的原理

---

差分进化算法是一种自组织最小化方法，利用种群中两个随机选择的不同向量来干扰现有向量，种群中的每一个向量都要进行干扰。

1. 它通过把种群中的两个成员之间的加权差向量加到第三个成员上来产生新的参数向量，该操作成为“变异”。
2. 将变异向量的参数与另外预先确定的目标向量参数按一定规则混合来产生实验向量，该操作成为“交叉”；
3. 若实验向量的代价函数比目标向量的代价函数低，实验向量就在下一代中替代目标向量，该操作成为“选择”；

差分进化算法流程

---

具体步骤如下：

1. 确定差分进化算法的控制参数和所要采用的具体策略。控制参数包括：种群数量、变异算子、交叉算子、最大进化代数、终止条件等。
2. 随机产生初始种群，进化代数k=1；
3. 对初始种群进行评价，即计算初始种群中每个个体的目标函数值。
4. 判断是否达到终止条件或达到最大进化代数；若是，则进化终止，将此时的最佳个体作为解输出；否则，继续下一步操作。
5. 进行变异操作和交叉操作，对边界条件进行处理，得到临时种群。
6. 对临时种群进行评价，计算临时种群中每个个体的目标函数值。
7. 对临时种群中的个体和原种群中对应的个体，进行“一对一”的选择操作，得到新种群。
8. 进化代数k=k+1,转步骤（4）.

实例：

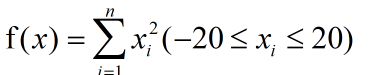
$$计算函数的最小值，其中个体x的维数n=10.这是一个简单的平方和函数，只有一个极小点x=(0,0,...,0)。$$

%%%%%%%差分进化求函数极值%%%%%%%%%
%%%%%%%初始化%%%%%%%%
clear all;
close all;
clc;
NP = 50;       %种群的数量
D = 10;        %变量的维度
G = 200;       %最大进化代数
F0 = 0.4;      %初始变异算子
CR = 0.1;      %交叉算子
Xs = 20;                            %上限
Xx = -20;                           %下限
yz = 10^-6;                         %阈值
%%%%%%%%赋初值%%%%%%%%%%%%
x = zeros(D,NP);                    %初始种群
v = zeros(D,NP);                    %变异种群
u = zeros(D,NP);                    %选择种群
x = rand(D,NP) * (Xs-Xx) + Xx;      %赋初值
%%%%%%%%%%计算目标函数%%%%%%%%%%%
for m = 1:NP
   Ob(m) = func1(x(:,m));
end
trace(1) = min(Ob);
%%%%%%%%%差分进化循环%%%%%%%%%%
for gen = 1:G
   %%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%
   %%%%%%%%%%%自适应变异算子%%%%%%%
   lamda = exp(1-G/(G+1-gen));
   F = F0*2^(lamda);
   %%%%%%%%r1,r2,r3和m互不相同%%%%
   for m = 1:NP
      r1 = randi([1,NP],1,1);
      while(r1 == m)
          r1 = randi([1,NP],1,1);
      end
      r2 = randi([1,NP],1,1);
      while (r2 == m) | (r2 == r1)
          r2 = randi([1,NP],1,1);
      end
      r3 = randi([1,NP],1,1);
      while (r3 == m) | (r3 == r1 | r3 == r2)
          r3 = randi([1,NP],1,1);
      end
      v(:,m) = x(:,r1) + F * (x(:,r2) - x(:,r3));
   end
   %%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%
   r = randi([1,NP],1,1);      %确保必有一个v(:)进入u(:)中
   for n = 1:D
      cr = rand(1);
      if (cr <= CR) | (n == r)
         u(n,:) = v(n,:);       %批量操作，替换所有个体第n维
      else
          u(n,:) = x(n,:);
      end
   end
   %%%%%%%%%%%%%%%%边界条件的处理%%%%%%%%%%%%%%%
   for n = 1:D
      for m = 1:NP
         if (u(n,m) < Xx) | (u(n,m) > Xs)
            u(n,m) = rand * (Xs - Xx) + Xx;
         end
      end
   end
   %%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%
   for m = 1:NP
      Ob1(m) = func1(u(:,m));
   end
   for m = 1:NP
      if Ob1(m) < Ob(m)
         x(:,m) = u(:,m);
      end
   end
   for m = 1:NP
      Ob(m) = func1(x(:,m));
   end
   trace(gen+1) = min(Ob);
   if min(Ob) < yz
      break;
   end
end
%%%%%%%%%%%%%%%%画图%%%%%%%%%%%%%%%
figure
plot(trace);
xlabel('迭代次数');
ylabel('目标函数值');
title('DE目标函数曲线');
%%%%%%%%%%%%%%适应度函数%%%%%%%%%%
function result = func1(x)
summ = sum(x.^2);
result = summ;
end