旋转子段 （思维stl）

题目：

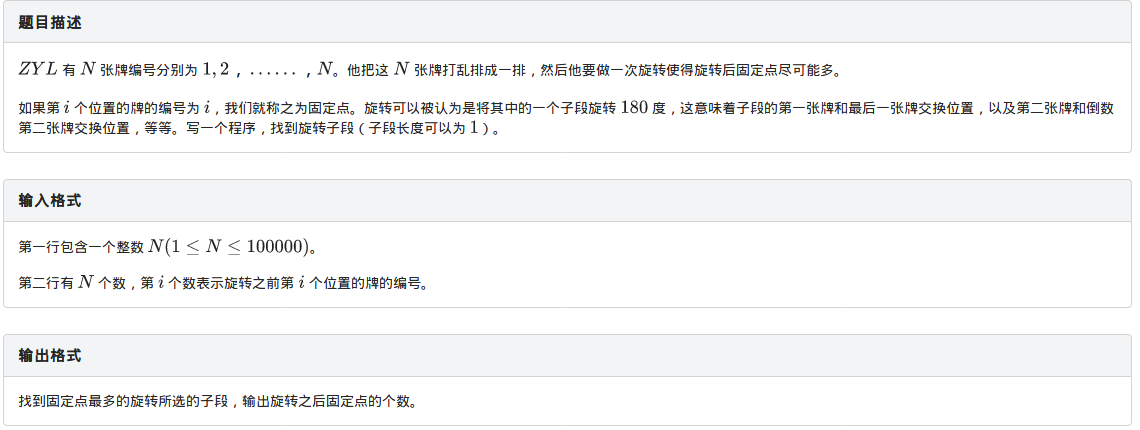
大概意思就是给你一个序列，你可以选择一段区间使它左右翻折一遍，然后呢，从1到n找一遍，看a[i]==i的数最多是多少。

其实刚才我已经把暴力思路说出来了，枚举每一个区间长度，枚举每一个左端点，再查询a[i]的值，时间复杂度O(n^3^)。

稍微优化一点，枚举每一个中点，左右扩展的同时查询，复杂度O（n^2^）(注意中点有可能不是点，可能是两个点中间，不考虑这个会被卡20分)

正解：

我们需要考虑下面两个性质：

性质1：对于一个点i，如果想让它满足条件，它的翻折区间是从i到a[i],在这个区间内满足a[k]+k==a[i]+i的点会在i翻折的同时也翻折到正确的位置，不满足的一定不会翻到正确的位置。

证明：显然，关于（a[i]+i）/2对称的点，一定满足(a[k]+k)/2==(a[i]+i)/2，只有满足这个条件k跟i才共用同一个中点，从而能一起翻折到正确的位置，不满足这个条件的一定翻不到正确的位置

我们对于所有的a[i]+i值，开一个向量存储所有的i。简而言之，就是开一个向量数组，把a[i]+i相同的元素都放到一个向量里面。

我们对于每一个向量，先根据翻折区间的大小，从小到大排序一遍，我们先处理小区间，再处理大区间（因为大区间会顺便把小区间的也翻折过去，会漏一些情况）。

对于每一个翻折区间，我们的结果是：

区间左侧的满足条件的i+区间右侧的满足条件的i+区间内翻折后满足条件的i（废话连篇）

对于区间左侧与右侧的满足条件的i，我们可一通过预处理（前缀和+后缀和）来做到O(1)查询，关键在怎么处理这个区间内的情况，这需要我们的下一个性质。

性质2：

一个区间内部的满足条件的i的数量与这个区间是满足a[i]+i相等的区间的正序排序位置相等（好复杂）

上面是我胡编的性质，我们处理这个性质需要结合刚才的vector来考虑。

对于一些a[i]+i相等的数们，我们把他们都放进了一个vector里面，然后都排序好了，然后这个i是排完序后的第几位，i～a[i]这个区间里面就有几个满足条件的数。

？？？是不是很神奇，竟然这么简单？下面是证明

对于相等a[i]+i的最小的区间，我们不妨设他为k~a[k]，已知它是最小的满足a[k]+k=a[i]+i的区间，那在这个区间翻折后，也之可能有这一个k变成了满足条件的数。首先，我们知道，只有a[i]+i=a[k]+k的区间通过这个翻折才能变为满足i=a[i]的数，而k～a[k]的区间是等值的区间中最小的那个，所以在k～a[k]以内的数，只能不满足a[i]+i=a[k]+k，（满足的都比k～a[k]这个区间大）

所以，k~a[k]这个区间翻折之后也就只有一个满足条件的i就是k啦。

以此类推，第二大的区间内部也只有那个区间的两端和这个k满足条件，翻折后满足条件的i有2个。

第三大的区间里翻折后满足条件的有3个，第四大的有4个……

所以我们知道对于a[i]+i相等的区间，第几大的区间翻折后区间里面就有几个满足条件a[i]==i的数。

思路差不多了上代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+10;
int n,a[maxn],L[maxn],R[maxn];//L数组是从1到i的满足a[i]==i的数量，R数组是i到n的
vector<int> q[maxn];
int now;
bool cmp(int x,int y){
	return abs(now-2*x)<abs(now-2*y);
	//now是现在的a[i]+i的和，翻折区间的长度=abs(a[i]-i)=abs(ans-i-i);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		q[a[i]+i].push_back(i);//记住这里的向量里面保存下标
		if(a[i]==i)L[i]=L[i-1]+1;
		else L[i]=L[i-1];
	}
	for(int i=n;i>=1;i--){
		if(a[i]==i)R[i]=R[i+1]+1;
		else R[i]=R[i+1];
	}
	//以上是初始化操作
	int ans=0;
	for(int i=2;i<=2*n;i++){
		now=i;
		if(q[i].empty())continue;
		sort(q[i].begin(),q[i].end(),cmp);
		for(int j=0;j<q[i].size();j++){
			int l=q[i][j],r=now-q[i][j];//当前区间的左右端点
			if(l>r)swap(l,r);
			ans=max(ans,L[l-1]+R[r+1]+j+1);
			//因为j=0的时候是第一个区间，所以加的是j+1。
		}
	}
	printf("%d",ans);
	return 0;
}