剑指 Offer 68 - II. 二叉树的最近公共祖先 + 最近公共祖先（LCA）

剑指 Offer 68 - II. 二叉树的最近公共祖先

Offer_68_2

题目详情

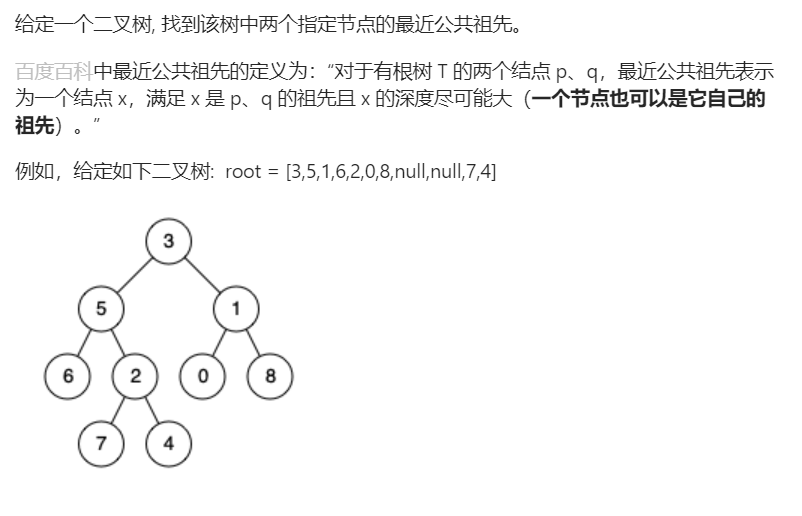
题解分析

java代码

package com.walegarrett.offer;
/**
 * @Author WaleGarrett
 * @Date 2021/2/16 14:01
 */

/**
 * 题目描述：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
 */
public class Offer_68_2 {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null || root==p || root==q)
            return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null)//至少有一个在右子树
            return right;
        if(right == null)//至少有一个在左子树
            return left;
        //左右子树均不为空表示找到公共祖先，p和q必分散在左右子树
        return root;
    }
}

复杂度分析

• 时间复杂度 O(N) ： 其中 N 为二叉树节点数；最差情况下，需要递归遍历树的所有节点。
• 空间复杂度 O(N) ： 最差情况下，递归深度达到 N ，系统使用 O(N) 大小的额外空间。

题解参考面试题68 - II. 二叉树的最近公共祖先（后序遍历 DFS ，清晰图解）