【译】Optaplanner开发手册本地化: (0) - 前言及概念

　　在此之前，针对APS写了一些理论性的文章；而对于Optaplanner也写了一些介绍性质，几少量入门级的帮助初学者走近Optaplanner。在此以后，老农将会按照Optaplanner官方的用户手册的结构，按章节地对其进行翻译，并成型一系列的操作说明文章。在文章中，为了降低对原文的理解难度，有些地方我不会直接按原文档的字面翻译，而是有可能加入一些我自己的理解，或添一些解释性的内容。毕竟英语环境下的思维和语言表达方式，跟中文或多或少会有差别的，所以如果全部按字面翻译，内容就非常生硬，可读性差，解程难度较大。我认为应该在理解了作者原意的基础上，再进一步以中文方式的表达，才算是真的的本地化。记得老农还是少农时，学习开发技术，需要阅读一些外国书箱的翻译本时，印象最深的是候捷老师的书，尽管《深入浅出MFC》，砖头厚度的书，硬是被我翻散了线，MFC尽管真的晦涩难懂，但候老却能把Windows的消息机制及MFC中整个个宏体系，系统地通俗地描述出来，令读者不需要花费太多精力去理解猜测书中字面的意义，大大降低的VC++中MFC的学习门槛。但老农毕竟只是一个一线开发人员，不是专业的技术资料翻译人才，不可能有候老师的专业水平，因此，我也只可尽我所能把内容尽量描述得通俗一些，让读者尽量容易理解，花费更少的时间掌握这些知道要点。

本文以Optaplanner 7.10.0 Final版本的开发手册作为基础进行翻译。

1. Optapplanner 介绍

1.1. 什么是Optaplanner?

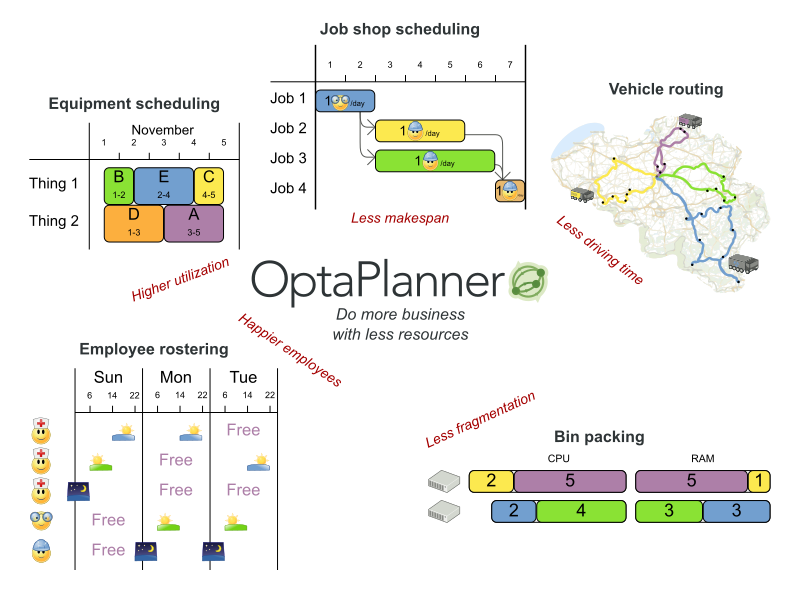
　　每个组织都需要面对规划、排程问题：在有限的资源约束下提供服务与产品（例如人员，资产，时间及资本等限制）。Optaplanner可以优化这类规划、排程问题，令到使用它的组织可以用更少的资源做更多的事（尽可能的花少钱办大事）。这就是著名的的约束满足规划，它属于运筹学的一部分。

Optaplanner是一个轻量的、可嵌入的，可以对规划问题进行优化的约束满足引擎，它可以解决案例有：

• 员工排班：为护士、维修工等人员制定上班时间表。
• 方程安排：安排会议、约见、维修工作、广告时间等。
• 教育领域的时间安排：安排课程、课堂、考试、会议讲座等。
• 规划车辆运动路线：通过已知的地图工具，为货运、客运（货车、火车、轮船、航班等）规划交通工具多目标的运行路线。
• 装箱问题：向容器、货车、轮船和仓库装载货物，同时可以规划电脑的资源加载利用，例如云计算的资源分配问题。
• 车间生产安排：规划汽车组装生产线，机器队规划，劳动任务的规则等。
• 下料问题：在下料分割的时候，实量最小的浪费，例如切割纸张、钢铁、地毯等。
• 运动赛事安排：规划比赛和训练，例如安排足球联赛、棒球联赛等。
• 金融优化：投资组合优化、实现风险分散等。

1.2. 什么是规划问题？

　一个规划问题，基于有限的资源和指定的约束，有一个优化目标。优化目标可以是多种事物，例如：

• 利润最大化 - 优化目标得出的结果是尽可以高的利润。
• 最小化生态足迹（即尽可能减少对生态的影响） - 优化目标是对环境产生尽可能小的影响。
• 最大化员工或客户的满足度 - 优化目标重视员工与客户的需要。

实现这些目标的能力依赖于可用资料的数量，例如：

• 人员数量
• 时间
• 预算
• 特殊资产，例如机台，车辆，计算机，建筑物等。

与这此资源相关的约束也必然计算在内，例如，一个人的工作小时数， 他们可使用（操作）的机台数量，设备之间的兼容性等。

Optaplanner可以帮助Java程序员有效地解决约束满足问题， 在Optaplanner引擎中，对每个有效的约束分数计算中，组合了启发式和元启发式算法。

1.2.1 规划问题属于NP-Complete问题或NP-hard问题

　　上述所有的案例或许都属于NP-complete/NP-hard问题，（什么是NP-Complete/NP-hard问题呢？），在外行人看来，它的定义是：

　　对于一个问题：

• 在合理时间内可以容易地验证一个给定的解。
• 在合理时间内，目前尚没有行之有效的解法，能找到其绝对最优解(注1)。

　　(注1)：至少，到目前为止，仍未有一个世界上最聪明的计算机科学家能找到此方法。可是一旦他们找到对其中一个NP-Complete问题的有效解法，那么这个方法对所有NP-Complete问题都是可行办法。事实上，如果任何人只需证明是这种解法的存在与否，即可获得100万美元的奖励。

　　其实这其含义是相当悲观的：要解决这些问题或许比你预想中更困难，因为目前针对这种问题的常见两种技术是未足够解决此类问题的。这两种方法是：

• 暴力算法(尽管是一些优化过，相对聪明的暴力算法变种), 但获得其解所需的时间非常长(译者：主要原因是时间复杂度非常高)。
• 快速算法，例如在Bin packing问题中，先装入最大项；但得到的解离绝对最优解仍存在相当大距离的。

通过使用一些更高级的算法，Optaplanner可以在合理的时间内，对这些规划问题找到相对较优解。

1.2.2 规划问题存在约束（包括硬约束与软件约束)

　　通常来说，一个规划问题至少包括两个层次的约束：

• (负面)硬约束，不可被违反。例如：一个教师在同节的时间内不能同时上两门课。
• (负面)软件约束，若可避免，它不应该被违反。例如：教师都不太喜欢在周五下午上课。

　　也有些问题存在一些正面的约束：

• 正面分数在可能情况下应该实现。例如：教师B喜欢在周一上午上果。

　　一些比较基础的规划问题(例如8王后问题)，只存在硬约束；有一些规划问题则存在超3层，甚至更多层次的约束。例如：硬约束，中间约束和软约束。

　　这些约束会被定义在规划问题的Score calculation里(也称为适应度函数)里。规划问题里的每一个解的优劣，都可以通过分数来评价。在Optaplanner中，分数约束是通过面向对象语文编写的，例如Java代码或通过Drools脚本实现的rules. 这些代码相当容易编写，灵活且易于扩展。

1.2.3 规划问题存在巨大的搜索空间

　　一个规划问题存在非常多的解，这些解可以分为以下数种：

• 可能解：规划问题的任意一个解都称作可能解，无论这个解是否违反了约束，或违反了多少约束。规划问题往往存在令人难以至今的巨量可能解，这里面很多解是毫无价值的。
• 可行解：规划问题的可行解是指没有违反任何（负面）硬约束的解。一个规划问题的可行解的数量，与其可能解相关。有时也不存在可行解，一个规划问题的每一个可行解，都是该问题的一个可能解。
• 绝对最优解:绝对最优解是这个规则问题获得约束分最高的那个解。规划问题通常只有1个或少量数个绝对最优解。通常存在至少1个绝对最优解，尽管当这个规划问题不存在可行解，它也存在绝对最优解，这时候绝对最优解就是非可行解。
• 相对最优解:相对最优解是指规划问题在一定的求解时间内得到评分最高的解。相对最优解通常是可行解，只要有足够的运行时间，找到的相对最优解就是绝对最优。

　　此外，尽管基于一个较小的数据集描述的一个规划问题，其可能解的数量通常是非常巨大的（如果计算正确的话）。正如你从示例中可以看到，大多数情况下，一个规划问题的可能解数量，对目前已知宇宙的原子数量还要多(10的80次方)。因为目前还没有直接的办法找出规划问题的绝对最优解，一些求解实现方法是通过暴力穷举的方法，至少可以穷举所有可能解中的一个子集。

　　OptaPlanner支持多种优化算法，以有效地涉足大量可能解，根据不同使用场景的情况，一些优化算法的性能比其它算法更佳，但哪个更佳是无法预先告知的（译者：需要通过Benchmark等功能测定）。在Optaplanner里，很容易能过修改几行XML内容或Java code，来更改求解器的配置，从而切换不同的优化算法。

【未完，待续...】

原创不易，如果觉得文章对你有帮助，欢迎点赞、评论。文章有疏漏之处，欢迎批评指正。

---

本系列文章在公众号不定时连载，请关注公众号（让APS成为可能）及时接收,二维码：

如需了解更多关于Optaplanner的应用，请发电邮致：kentbill@gmail.com
或到讨论组发表你的意见：https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信（13631823503）或QQ(12977379)实时沟通，但因本人日常工作繁忙，通过微信,QQ等工具可能无法深入沟通，较复杂的问题，建议以邮件或讨论组方式提出。(讨论组属于google邮件列表，国内网络可能较难访问，需自行解决)