LuoguP2617 Dynamic Rankings (动态主席树学习理解)

题目地址

题目链接

题解

动态主席树的板子题。动态主席树其实和静态的有很大差别，虽然同样是n个根，但是节点并不能共用，每个根节点表示bit上的一段区间。

所以其实是个树套树的东西来着，外层是bit，内层是主席树。

然后将所有数离散（包括读入进来的修改的数，所以动态主席树其实是离线的），那么就映射成了一段连续区间，用主席树维护这段区间。

每次修改就把x->n(+=lowbit(x))的所有节点的数v的那条链加上v，注意动态开点，不然空间爆炸。这样子 空间就是 \(nlog^2n\)的（每次修改只会动到一条链，一共动log条，所以是\(log^2\)的）。可以看一下下面这个图，很形象。



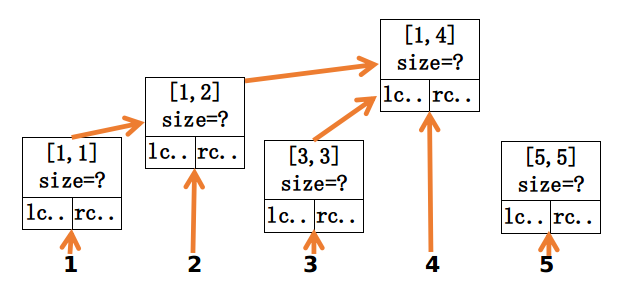
（图片来源于Flash_Hu）

每次查询将l-1和r两个点的前缀和在bit上面对应的节点找出来（log个），然后在主席树上向下走，一次同时减l-1对应的log个主席树，同时加r对应的log个主席树。

这样子时间复杂度是\(O(nlog^2n)\)。

大概就是这样...然后查询可以写成类似二分的写法，就可以非递归找了。但是修改还是写成递归的靠谱一点（非递归要写指针，指针容易写挂..）。还有注意每次修改要修改的是离散化后的值，但是输出要输出离散前的。

再看个代码意会一下应该就没问题了...

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200100, M = 40000100;

int a[N], b[N], len;
int l[N], r[N], op[N], d[N];
int n, m, root[N], rootl[30], rootr[30], tot;
struct tree {
	int lc, rc, sum;
}t[M];

#define lowbit(i) (i&(-i))
void upd_tree(int &rt, int l, int r, int pos, int v) {
	if(!rt) rt = ++tot; t[rt].sum += v;
	if(l == r) return;
	int mid = (l + r) >> 1;
	if(pos <= mid) upd_tree(t[rt].lc, l, mid, pos, v);
	else upd_tree(t[rt].rc, mid + 1, r, pos, v);
}

void upd(int pos, int k, int v) {
	for(int i = pos; i <= n; i += lowbit(i)) {
		upd_tree(root[i], 1, len, k, v);
	}
}
#define lc(i) (t[i].lc)
#define rc(i) (t[i].rc)
int query(int L, int R, int k) {
	int sum = 0, cur_l = 0, cur_r = 0;
	for(int i = L - 1; i; i -= lowbit(i)) rootl[++cur_l] = root[i];
	for(int i = R; i; i -= lowbit(i)) rootr[++cur_r] = root[i];
	int l = 1, r = len;
	while(l != r) {
		int mid = (l + r) >> 1; sum = 0;
		for(int i = 1; i <= cur_r; ++i) sum += t[lc(rootr[i])].sum;
		for(int i = 1; i <= cur_l; ++i) sum -= t[lc(rootl[i])].sum;
		if(k <= sum) {
			r = mid;
			for(int i = 1; i <= cur_l; ++i) rootl[i] = lc(rootl[i]);
			for(int i = 1; i <= cur_r; ++i) rootr[i] = lc(rootr[i]);
		}
		else {
			l = mid + 1, k -= sum;
			for(int i = 1; i <= cur_l; ++i) rootl[i] = rc(rootl[i]);
			for(int i = 1; i <= cur_r; ++i) rootr[i] = rc(rootr[i]);
		}
	}
	return b[l];
}
#undef lc
#undef rc

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; ++i) scanf("%d", &a[i]), b[++len] = a[i];
	for(int i = 1; i <= m; ++i) {
		char ch[5];
		scanf("%s%d%d", ch, &l[i], &r[i]);
		op[i] = ch[0] == 'Q';
		if(op[i]) scanf("%d", &d[i]);
		else b[++len] = r[i];
	}
	sort(b+1,b+len+1); len = unique(b+1,b+len+1)-b-1;
	for(int i = 1; i <= n; ++i) a[i] = lower_bound(b+1,b+len+1,a[i])-b;
	for(int i = 1; i <= n; ++i) upd(i, a[i], 1);
	for(int i = 1; i <= m; ++i) {
		if(!op[i]) {
			upd(l[i], a[l[i]], -1);
			a[l[i]] = lower_bound(b+1,b+len+1,r[i])-b;
			upd(l[i], a[l[i]], 1);
		} else {
			printf("%d\n", query(l[i], r[i], d[i]));
		}
	}
	return 0;
}