java-数组排序--计数排序、桶排序、基数排序
计数排序引入
不难发现不论是冒泡排序还是插入排序,其排序方法都是通过对每一个数进行两两比较进行排序的,这种方法称为比较排序,实际上对每个数的两两比较严重影响了其效率,理论上比较排序时间复杂度的最低下限为nlog(n),即任何比较排序的时间复杂度将不会低于nlog(n),那么有没有方法能不经过数列比较就能使数列排序呢 ,她们的时间复杂度又是多少呢???
计数排序就是一个非比较排序的算法,一如鱼与熊掌不可兼得,她使用了牺牲空间换时间的方法,使的时间复杂度可以达到Ο(n+k)
假设我们有一个数列arr=[3,4,6,4,8,1] 假设max为数列的最大值,此时我们创建一个大小为max+1的辅助数组sortArr,我们以此遍历arr数组,并将数列中的数对应辅助数组sortArr下标的值+1
那么辅助数组中的数,就是其下标在待排序数组中出现的次数,最后我们通过遍历辅助数组sortArr就能获得一个排序好的序列(为什么要创建max+1长度的辅助序列:因为要将待排序数列与辅助序列的下标进行关联,而max应为辅助序列的最后一个下标值,而序列的下标从0开始,有辅助序列的长度应为max+1)
上图
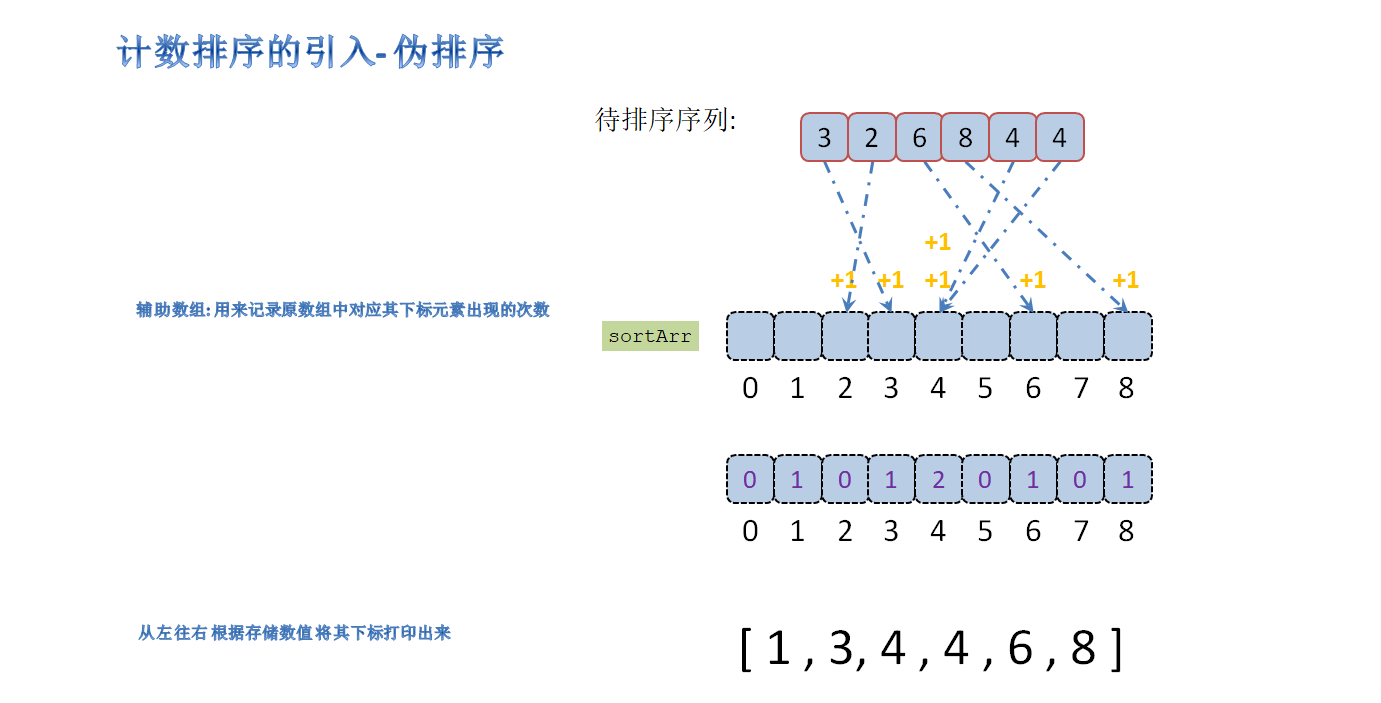
代码:
public static void countSort01(int[] arr) {
/* 获取序列的最大值 */
int max=arr[0];
for (int i = 0; i < arr.length; i++) {
if(arr[i]>max) {
max=arr[i];
}
}
/* 创建一个长度为max+1的辅助数组 用来存储与辅助数组对应下标的数值 在待排序数列中出现的次数 */
int[] sortArr=new int[max+1];
for (int i = 0; i < arr.length; i++) {
/* 遍历带排序数列 每次将辅助序列对应下标处的数值+1 */
sortArr[arr[i]]++;
}
/* 打印辅助序列 与 排序数 */
System.out.println(Arrays.toString(sortArr));
for (int i = 0; i < sortArr.length; i++) {
for (int j = 0; j < sortArr[i]; j++) {
System.out.print(i+" , ");
}
}
}
测试一下
public static void main(String[] args) {
Sort.countSort01(new int[] {6,10,6,8,6,8,12,15,9,6,7});
}
结果:
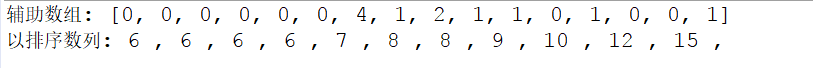
对引入的改进
从上面看,我们已经能对一个数组进行基本的排序了,但是仔细想想,此时打印的排序的数是不稳定的,甚至于这个数与原数列失去的联系,它仅仅只是表示辅助数列的一个下标值,如果我们是对一个对象进行排序,比如学生[姓名,成绩],通过上种方法只能排出所有的成绩,而原来此成绩是谁的却无从得知了,无疑这样的排序不那么合格,此时,我们对代码进行一些改进 这次我们不再存储出现数字的个数,而是存储其在已排序数组中的位置
图片
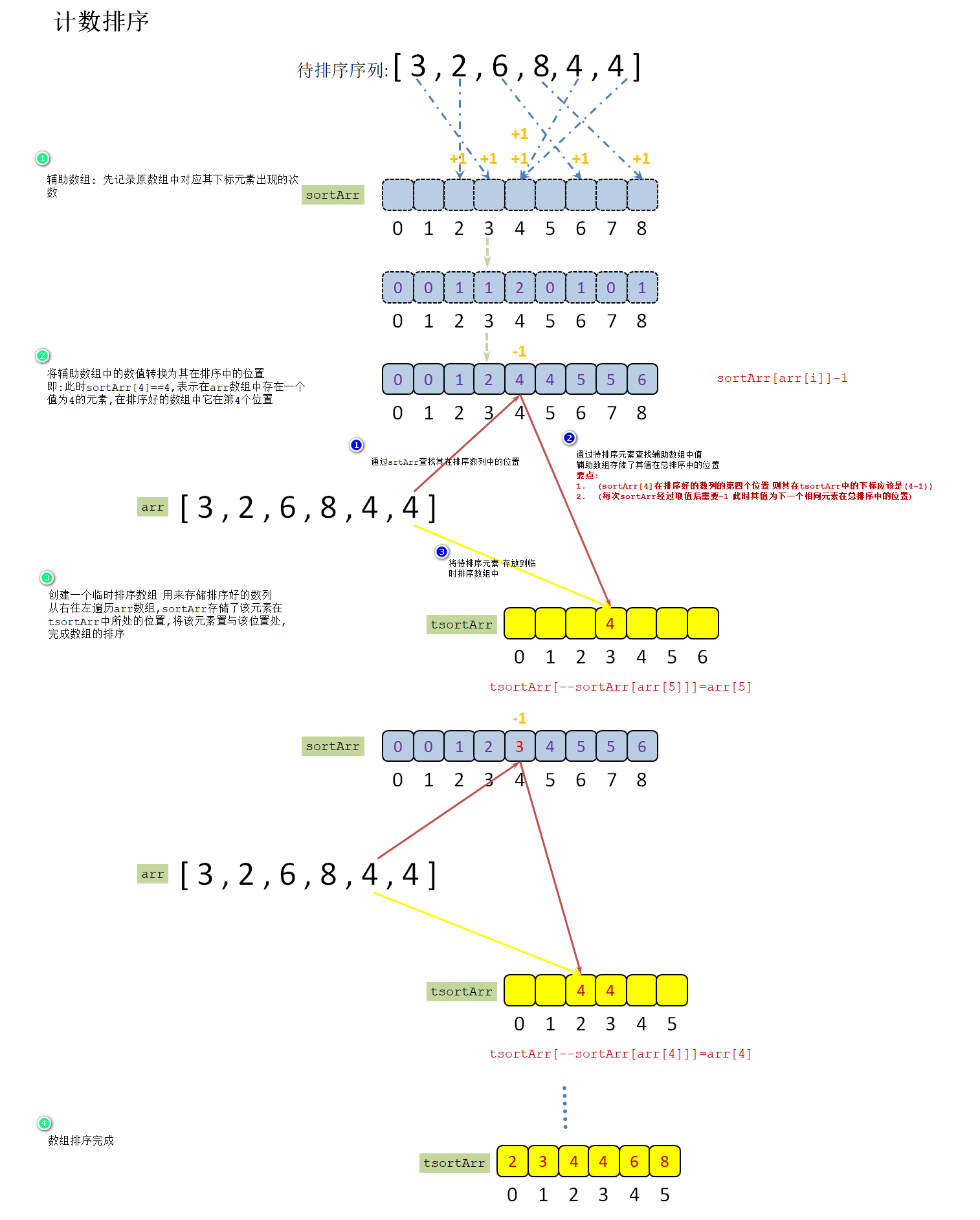
代码:
public static void countSort02(int[] arr) {
/* 获取待排序数列的最大值 用来创建辅助数组 */
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
/* 创建辅助数组 先在辅助数组存储其对应下标在待排序数中出现的次数 (与countSort01同) */
int[] sortArr = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
sortArr[arr[i]]++;
}
/* 对辅助数组进行改进 将其存储的对应待排序数列的次数 转换为临时排序数列的下标位置 */
for (int i = 1; i < sortArr.length; i++) {
sortArr[i] += sortArr[i - 1];
}
System.out.println("辅助序列: "+Arrays.toString(sortArr));
/* 创建临时排序数列 并从右往左遍历arr将其顺序放于tsortArr */
int[] tsortArr = new int[arr.length];
for (int i = arr.length-1; i > 0; i--) {
tsortArr[--sortArr[arr[i]]] = arr[i];
}
System.out.println("排序数列: "+Arrays.toString(tsortArr));
}
这样我们就能获取一个排序数列了 测试一下
public static void main(String[] args) {
System.out.println("----------引入-------------");
Sort.countSort01(new int[] {6,10,6,8,6,8,12,15,9,6,7});
System.out.println();
System.out.println("----------改进-------------");
Sort.countSort02(new int[] {6,10,6,8,6,8,12,15,9,6,7});
}
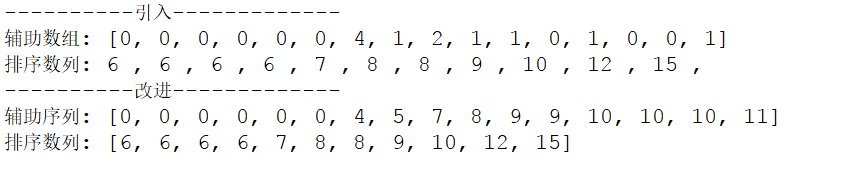
计数排序
因为算法创建了两个0-(max+1)的数组进行辅助,如果是象[2,1,4,5,8]这样的数列自然没有问题,但如果是对像[99,97,96,99,100]这样的数列进行排序 就会造成比较大的空间浪费了,所以我们只需要生成max-min+1长的辅助数组就ok啦
直接上代码
public static void countSort(int[] arr) {
/* 获取待排序数列的最大值,与最小值 用来创建辅助数组 */
int min=arr[0],max = arr[0];
for (int i = 0; i < arr.length; i++) {
if(arr[i]>max) {
max=arr[i];
}
if(arr[i]<min) {
min=arr[i];
}
}
/* 创建辅助数组 先在辅助数组存储其对应下标在待排序数中出现的次数 (与countSort01同) */
int[] sortArr = new int[max + 1];
sortArr=new int[max-min+1];
for (int i = 0; i < arr.length; i++) {
sortArr[arr[i]-min]++;
}
/* 对辅助数组进行改进 将其存储的对应待排序数列的次数 转换为临时排序数列的下标位置 */
for (int i = 1; i < sortArr.length; i++) {
sortArr[i]+=sortArr[i-1];
}
System.out.println("辅助序列: "+Arrays.toString(sortArr));
/* 创建临时排序数列 */
int[] tsortArr=new int[arr.length] ;
for (int i = arr.length-1; i > 0; i--) {
tsortArr[--sortArr[arr[i]-min]]=arr[i];
}
System.out.println("排序数列: "+Arrays.toString(tsortArr));
}
测试:
public static void main(String[] args) {
System.out.println();
System.out.println("----------引入-------------");
Sort.countSort01(new int[] {6,10,6,8,6,8,12,15,9,6,7});
System.out.println();
System.out.println("----------改进-------------");
Sort.countSort02(new int[] {6,10,6,8,6,8,12,15,9,6,7});
System.out.println();
System.out.println("----------计数排序-------------");
Sort.countSort(new int[] {6,10,6,8,6,8,12,15,9,6,7});
}

桶排序一
计数排序很快 但是却有一些限制
1.计数排序只能对整数进行排序,
2.当数列之间比较松散,最大最小之差比较大时会浪费比较大的空间浪费
桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))--百度百科
即桶排序创建多个桶区间 将处在同一区间范围的数放在一个桶里,然后再单独对每个桶中的数列进行排序 当然每个桶区间的范围是多大就需要看情况了 当桶的区间特别小 每一个桶只存储一个数 那么其时间复杂度就与计数排序差不多,单无疑需要花费大量的空间 而设置单个桶的区间太大 比如所有序列都落入到一个桶里,那么 其时间复杂度只取决于对单个桶进行排序的算法的复杂度了
先上图
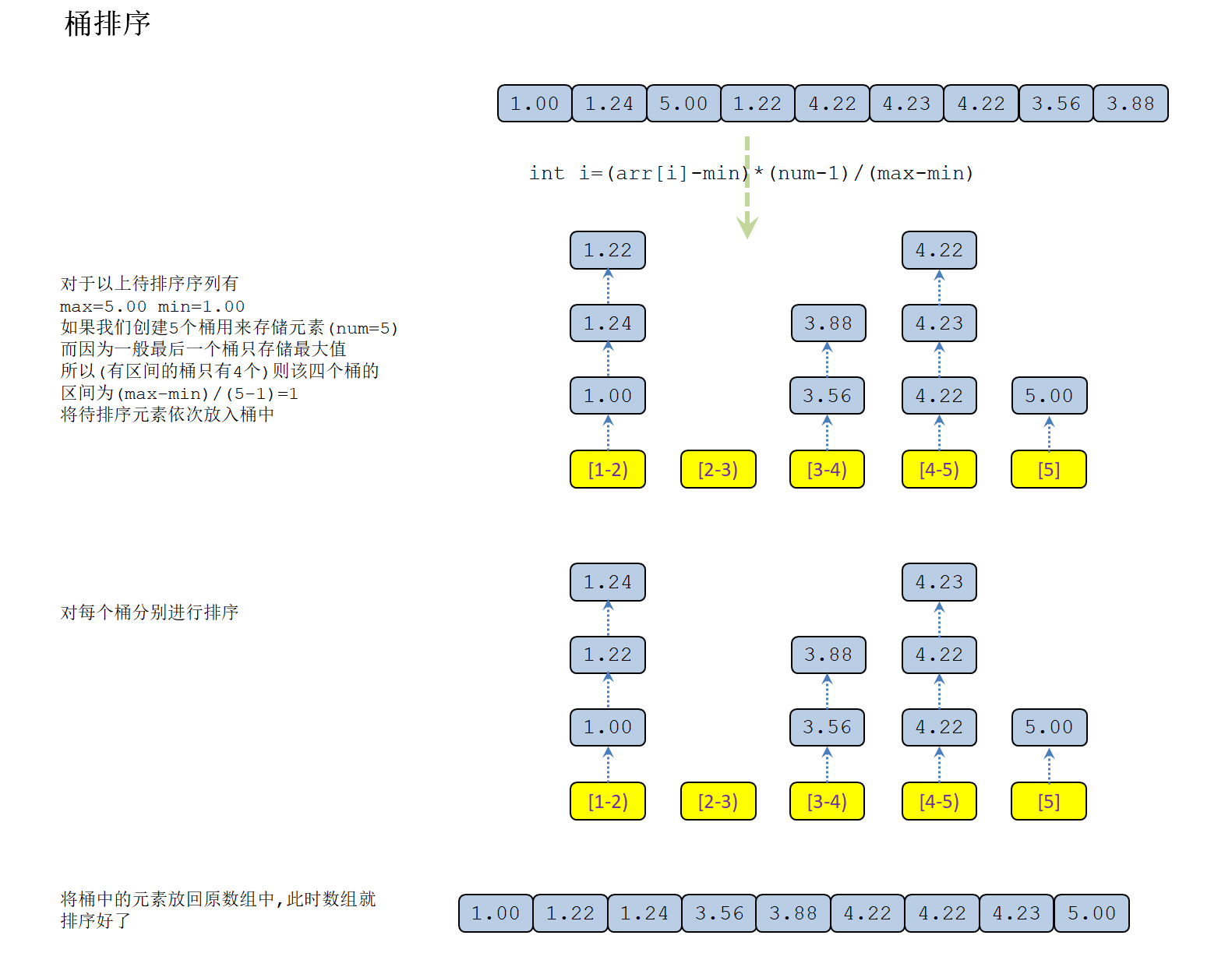
代码:
/**
* 桶排序 将待排序数列 放入n个桶中 对于每个数列有
* 最大值 max 最小值 min 桶数 n(最后一个桶只存储最大值) 所以(1-(n-1))中每个桶的区间大小应为(max-min)/(n-1)
* 此时有==> 元素i入桶的序列号为:int t=(arr[i]-min)*(n-1)/(max-min)
* @param arr 待排序数列
* @param n 桶数
*/
public static void buckSort(double[] arr,int n) { /* 创建n个桶 使用ArrayList作桶 */
List<Double>[] bucks=new ArrayList[n];
for (int i = 0; i < bucks.length; i++) {
bucks[i]=new ArrayList<>();
} /* 获取数列的最大值最小值 */
double max=arr[0],min= arr[0];
for (int i = 0; i < arr.length; i++) {
if(arr[i]<min) {
min= arr[i];
}
else if(arr[i]>max) {
max= arr[i];
}
} /* 将元素以此放入桶中 */
for (int i = 0; i < arr.length; i++) {
/* 计算元素该入哪个桶 */
int t=(int) ((arr[i]-min)*(n-1)/(max-min));
bucks[t].add(arr[i]);
}
/* 对每个桶单独排序 */
for (int i = 0; i < bucks.length; i++) {
Collections.sort(bucks[i]);
System.out.println(bucks[i]);
} /* 将桶中元素 放回原数组 */
for (int i = 0,k=0; i < bucks.length; i++) {
for (int j = 0; j < bucks[i].size(); j++) {
arr[k++]=bucks[i].get(j);
}
}
System.out.println("排序数列: "+Arrays.toString(arr));
}
测试
public static void main(String[] args) {
buckSort(new double[] {1.25,3.22,0.56,5.35,1.24,5.22,4.23,4.22,3.56,3.88,4.23},5);
}

桶排序中可能存在的两个小问题:
1. 计算桶区间时 为什么是(max-min)/(桶数-1)
我们直到如果将[1-5](最大值5 最小值1)的元素序列分为5个桶,那么我们如果按5计算区间范围,有区间大小=(5-1)/5==>0.8,那么我们按照此区间计算每个桶的范围:
[1,1.8), [1.8,2.6), [2.6,3.4), [3.4.4.2), [4.2,5) 此时我们发现5消失了!!! 此时再计算5的桶下标会得到 桶下标=(5-1)/0.8==>5 而我们生成了5个桶,最大下标只能到4,也就下标越界了,为了解决这个问题,我们使最后一个桶只存储一个数值(最大值),即只有四个桶是存在区间的,此时我们有桶:
[1-2),[2-3),[3-4),[4-5),[5] 再用5测试一下 桶下标=(5-1)/1==>4,完美!
2. 计算桶下标的方法int t=(int) ((arr[i]-min)*(n-1)/(max-min));是怎么来的?
当我们从上个问题知道了(n-1)代表有区间的桶时,就已经比较简单了,我们反推一下
(arr[i]-min)*(n-1)/(max-min)
= (arr[i]-min)/((max-min)/(n-1))
= (arr[i]-min)/区间大小
是的,一个数除以一个区间大小,不就表示该数在第几个区间(桶)嘛
桶排序二
上述桶排序用在一个固定区段的浮点数序列中,还是挺好的,但如果对[0-1)区间的序列进行排序,我们可以对其x10,使其变成一个[0-10)之间的无序数列,并将其按照个位数值,将其放入0-9的桶中
见图解
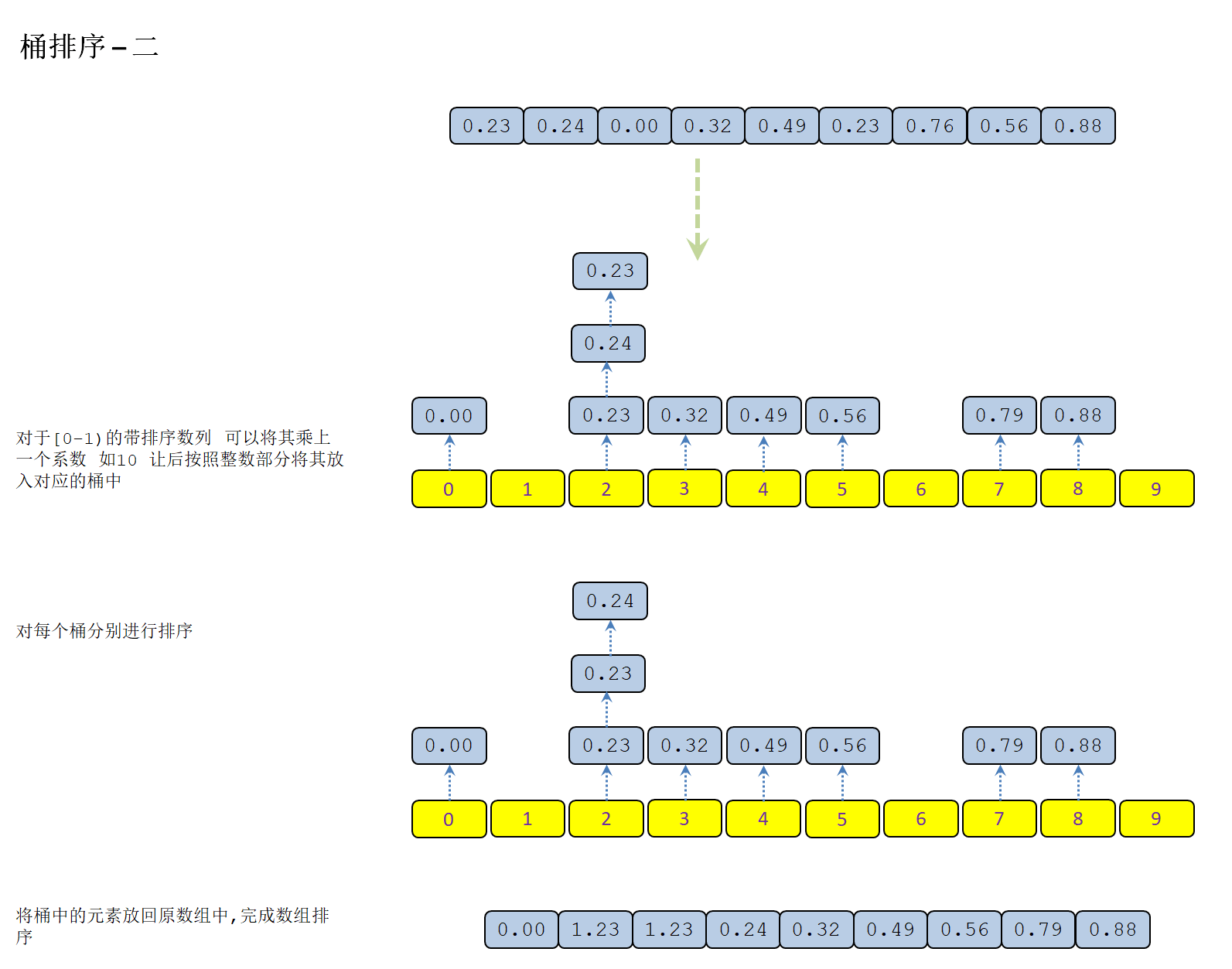
见代码
public static void buckSort(double[] arr) {
/* 创建10个桶 使用ArrayList作桶 */
List<Double>[] bucks=new ArrayList[10];
for (int i = 0; i < bucks.length; i++) {
bucks[i]=new ArrayList<>();
}
/* 遍历待排序数列 ,将其元素x10并放入相应的桶中 */
for (int i = 0; i < arr.length; i++) {
int t=(int) (arr[i]*10);
bucks[t].add(arr[i]);
}
/* 对每个桶单独排序 */
for (int i = 0; i < bucks.length; i++) {
Collections.sort(bucks[i]);
System.out.println("桶序列"+i+": "+bucks[i]);
}
/* 将桶中元素 放回原数组 */
for (int i = 0,k=0; i < bucks.length; i++) {
for (int j = 0; j < bucks[i].size(); j++) {
arr[k++]=bucks[i].get(j);
}
}
System.out.println("排序数列: "+Arrays.toString(arr));
}
测试
public static void main(String[] args) {
buckSort(new double[] {0.25,0.33,0.11,0.26,0.65,0.84,0.96,0.44});
}

基数排序
基数排序时根据基数不同 将不同的数分配到不同的桶中,(最低位优先)基数排序先对根据数列的个位数 将其放入0-9的二维数组中 然后以此对十位数 百位数等进行相同操作 最后得到一个有序数列,当然最高位优先其思想也是一样
上图片
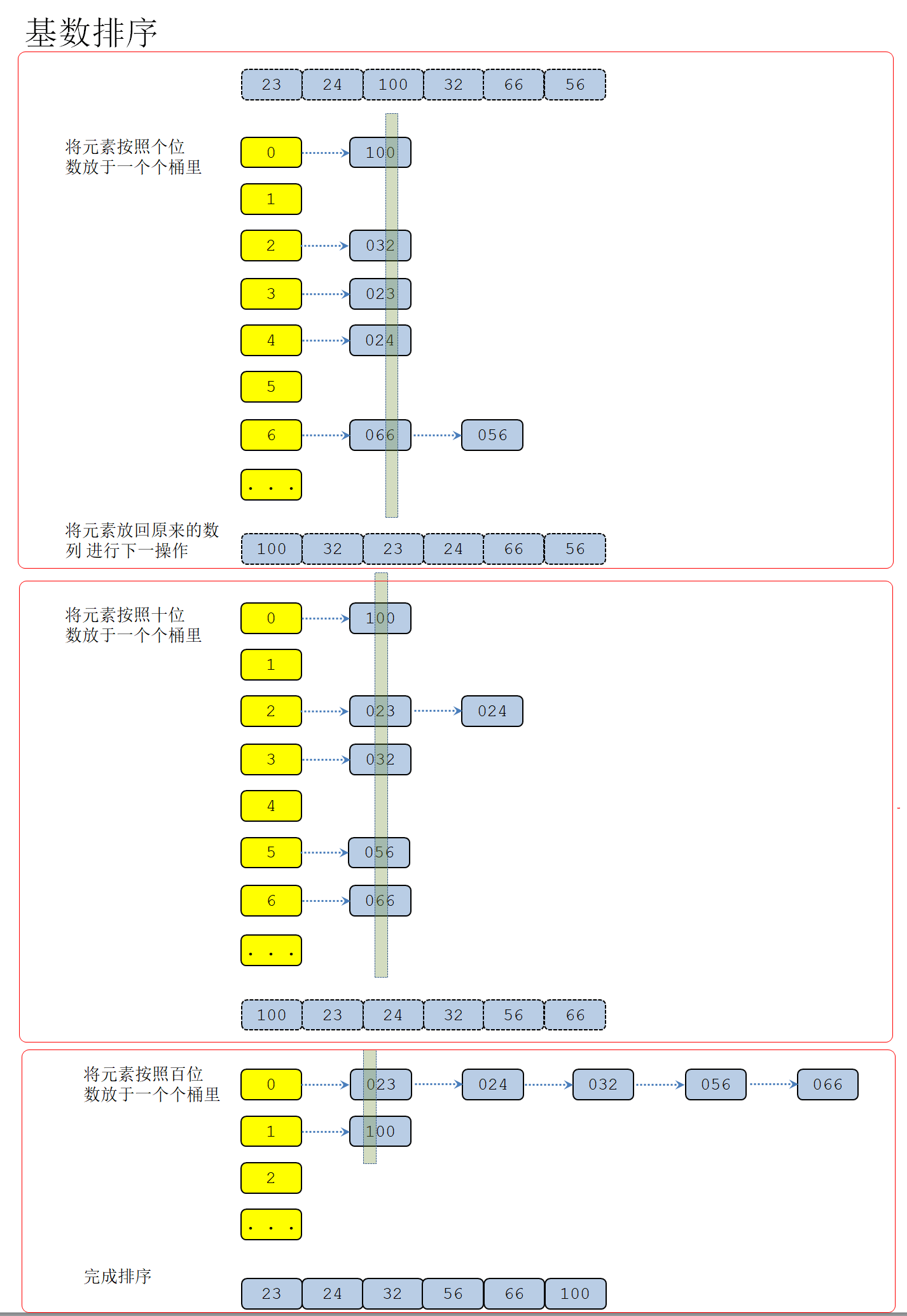
代码
public static void radixSort(int[] arr) {
/* 创建一个10*arr.length的二维数组 */
int[][] duck=new int[10][arr.length];
/* 先获取最大值 */
int max=arr[0];
for (int i = 0; i < arr.length; i++) {
if(arr[i]>max) {
max=(int) (arr[i]+1);
}
}
for (int i = 1; max>0 ; i*=10) {
/* 记录每个桶的下标 */
int[] count=new int[10];
for (int j = 0; j < arr.length; j++) {
int t=(arr[j]/i)%10;
duck[t][count[t]++]=arr[j];
}
/* 将桶中的数放回原数组 等待下一位数的排序 */
for (int j = 0,c=0; j < 10; j++) {
for (int k = 0; k < count[j]; k++) {
arr[c++]=duck[j][k];
}
}
max/=i;
}
System.out.println(Arrays.toString(arr));
}
测试
public static void main(String[] args) {
Sort.radixSort(new int[] {6,10,25,80,612,8,12,15,9,6,7});
}

参考:
桶排序一:漫画:什么是桶排序?
如果有地方写的错误,或者有什么疑问与建议,欢迎大家提出来 愿与大家一同进步
java-数组排序--计数排序、桶排序、基数排序的更多相关文章
- 记数排序 & 桶排序 & 基数排序
为什么要写这样滴一篇博客捏...因为一个新初一问了一道水题,结果就莫名其妙引起了战斗. 然后突然发现之前理解的桶排序并不是真正的桶排序,所以写一篇来区别下这三个十分相似的排序辣. 老年菜兔的觉醒!!! ...
- Python线性时间排序——桶排序、基数排序与计数排序
1. 桶排序 1.1 范围为1-M的桶排序 如果有一个数组A,包含N个整数,值从1到M,我们可以得到一种非常快速的排序,桶排序(bucket sort).留置一个数组S,里面含有M个桶,初始化为0.然 ...
- python 排序 桶排序
算法思想: 桶排序将数组分到有限数量的桶里.然后每个桶里再分别排序(使用任何算法) 当要倍排序的数组内的数值时均匀分配的时候,桶排序使用线性时间O(n) 步骤: 根据最大值.最小值.桶内数据范围设定一 ...
- 排序基础之非比较的计数排序、桶排序、基数排序(Java实现)
转载请注明原文地址: http://www.cnblogs.com/ygj0930/p/6639353.html 比较和非比较排序 快速排序.归并排序.堆排序.冒泡排序等比较排序,每个数都必须和其他 ...
- 计数排序和桶排序(Java实现)
目录 比较和非比较的区别 计数排序 计数排序适用数据范围 过程分析 桶排序 网络流传桶排序算法勘误 桶排序适用数据范围 过程分析 比较和非比较的区别 常见的快速排序.归并排序.堆排序.冒泡排序等属于比 ...
- 桶排序与基数排序代码(JAVA)
桶排序 publicstaticvoid bucketSort(int[] a,int max){ int[] buckets; if(a==null || m ...
- 桶排序和计数排序的理解实现和比较(Java)
比较和非比较的区别 常见的快速排序.归并排序.堆排序.冒泡排序等属于比较排序.在排序的最终结果里,元素之间的次序依赖于它们之间的比较.每个数都必须和其他数进行比较,才能确定自己的位置.比较排序的优势是 ...
- 计数排序与桶排序python实现
计数排序与桶排序python实现 计数排序 计数排序原理: 找到给定序列的最小值与最大值 创建一个长度为最大值-最小值+1的数组,初始化都为0 然后遍历原序列,并为数组中索引为当前值-最小值的值+1 ...
- 计数排序、桶排序python实现
计数排序在输入n个0到k之间的整数时,时间复杂度最好情况下为O(n+k),最坏情况下为O(n+k),平均情况为O(n+k),空间复杂度为O(n+k),计数排序是稳定的排序. 桶排序在输入N个数据有M个 ...
- Java算法 -- 桶排序
桶排序(Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里.每个桶再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序).桶排序是鸽巢排序 ...
随机推荐
- selenium各版本jar包下载地址
http://selenium-release.storage.googleapis.com/index.html
- apue——读目录操作
头文件: #define _POSIX_C_SOURCE 200809L #include <sys/types.h> #include <sys/stat.h> #inclu ...
- Apache Hadoop 2.9.2 的集群管理之服役和退役
Apache Hadoop 2.9.2 的集群管理之服役和退役 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 随着公司业务的发展,客户量越来越多,产生的日志自然也就越来越大来,可能 ...
- sass补充(2019-3-9)
@each 输出 格式: @each $var in value,value1,value2{ } eg: @each $var1 in 100px,200px,300px{ .box{ width: ...
- 原型模式-Prototype(Java实现)
原型模式-Prototype 通过复制(克隆.拷贝)一个指定类型的对象来创建更多同类型的对象. 就像去蛋糕店买蛋糕一样. 柜台里的蛋糕都是非卖品. 只是为顾客提供一种参照. 当顾客看上某一个样式的蛋糕 ...
- 【Unity游戏开发】tolua之wrap文件的原理与使用
本文内容转载自:https://www.cnblogs.com/blueberryzzz/p/9672342.html .非常感谢原作者慷慨地授权转载,比心!@blueberryzzz 是位大神,欢迎 ...
- [Deep Learning] 深度学习中消失的梯度
好久没有更新blog了,最近抽时间看了Nielsen的<Neural Networks and Deep Learning>感觉小有收获,分享给大家. 了解深度学习的同学可能知道,目前深度 ...
- Linux samba服务器的搭建
目录 1. 安装samba 2. 配置smb.conf 3. 创建samba登陆用户 4. 创建samba共享文件夹 5. 重启samba服务 6. 访问samba共享文件夹 7. 参考资料 1. 安 ...
- kail linux虚拟机安装tools工具
因为自己比较懒,有时候自己不想打字需要粘贴就安装了虚拟机tools工具,又因为自己脑子不好使所以就写一下步骤,以便以后用得着.我这里用得是kail linux系统,不知道contest能不能这样安,下 ...
- python—异常
异常是在程序中不可避免的,当程序遇到一个异常时程序就会停止,可以使用try—except进行处理异常,即便在出现异常程序也可以继续运行. 语法: try: 代码 except 异常名: 处理异常的代码 ...
