FFT学习笔记

快速傅里叶变换FFT(Fast Fourior Transform)

先说一下它能干嘛qwq

​ 傅里叶变换有两种，连续傅里叶变换和离散傅里叶变换，OI中主要用来快速计算多项式卷积。

等一下，卷积是啥》》

​ 卷积可以通俗地理解成把两个多项式相乘，比如 ： \((x^2+x)*(x+2)=x^3+2x^2+2x\)

​ 对于多项式的系数来说，就是求这个柿子：

​ 给定两个多项式 \(A(x), B(x):​\) ​

\[A(x)=\sum_{i=0}^{n-1} {a_ix^i}
\]

\[B(x)=\sum_{i=0}^{n-1} {b_ix^i}
\]

​ 相乘得到 \(C(x):​\)

\[C(x)=\sum_{j+k=i , 0 \leq j , k < n} {a_jb_kx^i}
\]

​ 直接暴力计算复杂度是 \(O(n^2),​\) 显然不够优秀\(,​\) 所以要用FFT快速计算\(;​\)

前置知识

​ 复数初步\(;\) 多项式表达 \(\ldots \ldots\)

正文部分

一、多项式的表达

​ 系数表达\(:\) 一般我们写的形如 \(x^2+5x-1\) 这样的柿子可以表示为向量 \(\vec {a}=(1,5,-1)\)

​ 点值表达\(:\) 给定\(n\)个点\(,\) 可以确定一个\(n-1\)次多项式\(;\) 一个多项式有无数种点值表达\(;\)

​ 将点值表达转换为系数表达的过程叫做插值\(,\) 常用的有拉格朗日插值法 \(;\)

​ 显然对于两个多项式的点值表达横坐标采样点相同\(,\) 就可以直接相乘，时间复杂度\(O(n)\)。

二、复数\((complex)\)初步 \(:\) 单位根

​ \(n\) 次单位根指满足 \(z^n=1\) 的复数，一共有 \(n\) 个\(,\) 即 \(\omega_n^k=e^{\frac{2 \pi ik}{n}}\) \(,\) $k \in [0 , n-1]; $ （强烈吐槽数学公式渲染qaq

​ 根据欧拉公式 \(e^{ik}=\cos(k)+i\sin(k)​\) \(,​\) 所以 \(\omega_n^k=cos(\frac{2k \pi}{n})+i\sin(\frac{2k \pi}{n});​\)

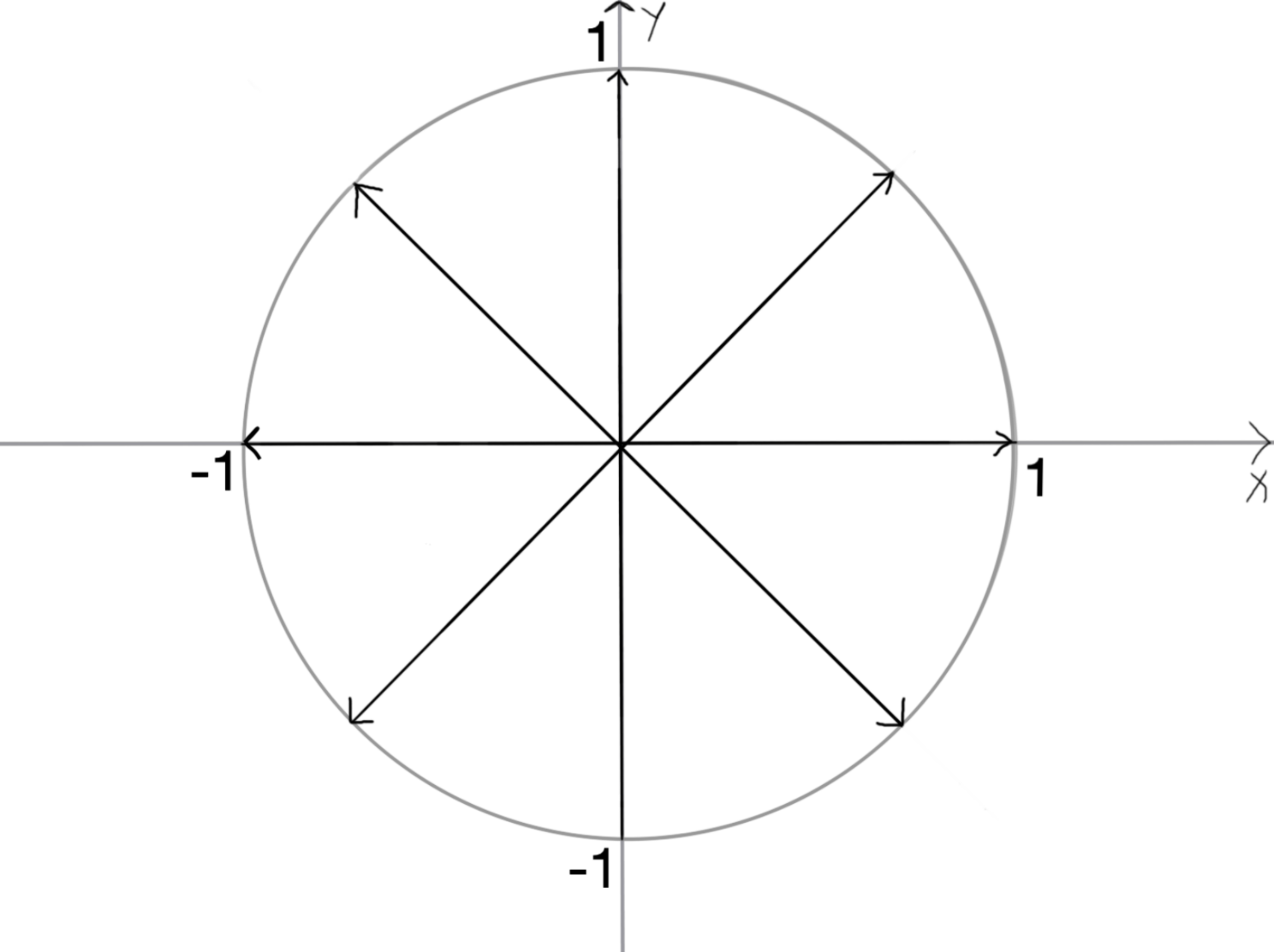
​ 几何意义\(:\) \(n\) 次单位根均匀分布在复平面的单位圆上\(;\) \(p.s.\) 复数相乘\(:\) 模长相乘\(,\) 幅角相加

​ \(n=8\) 时\(,\) 如下图\(:\)

三、DFT与IDFT

\(1.DFT\)

​ DFT$(Discrete $ \(Fourier\) \(Transform)\) 可以在 \(O(n\) \(lb\) \(n)\) 的时间内把多项式的系数表达转为点值表达\(;\)

​ 一个多项式的系数表达 \(\vec a=(a_0,a_1,a_2……a_n-1)\) 可以写成一个矩阵列向量\(a:\)

\[\left [
\begin{matrix}
a_0 \\
a_1 \\
a_2 \\
a_3 \\
\vdots \\
a_n-1
\end{matrix}
\right ]
\]

​ 把\(n​\)个单位复数根带入该多项式可以得到如下方程组\(;​\)

\[\begin{cases}
a_0(\omega_n^0)^0+a_1(\omega_n^0)^1+a_2(\omega_n^0)^2+\cdots+a_{n-2}(\omega_n^0)^{n-2}+a_{n-1}(\omega_n^0)^{n-1}=A_0 \\
a_0(\omega_n^1)^0+a_1(\omega_n^1)^1+a_2(\omega_n^1)^2+\cdots+a_{n-2}(\omega_n^1)^{n-2}+a_{n-1}(\omega_n^1)^{n-1}=A_1 \\
\vdots \\
a_0(\omega_n^{n-1})^0+a_1(\omega_n^{n-1})^1+a_2(\omega_n^{n-1})^2+\cdots+a_{n-2}(\omega_n^{n-1})^{n-2}+a_{n-1}(\omega_n^{n-1})^{n-1}=A_{n-1} \\
\end{cases}
\]

​ 其中\(,\) \(A\)即为点值表达；

​ 写成矩阵形式\(:\)

\[\left[
\begin{matrix}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & \cdots & (\omega_n^0)^{n-1} \\
(\omega_n^1)^0 & (\omega_n^1)^1 & (\omega_n^1)^2 & \cdots & (\omega_n^1)^{n-1} \\
(\omega_n^2)^0 & (\omega_n^2)^1 & (\omega_n^2)^2 & \cdots & (\omega_n^2)^{n-1} \\
\vdots & \vdots & \vdots& \vdots& \vdots\\
(\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & (\omega_n^{n-1})^2 & \cdots & (\omega_n^{n-1})^{n-1}
\end{matrix}
\right ]
\left[
\begin{matrix}
a_0 \\
a_1 \\
a_2 \\
\vdots \\
a_{n-1}
\end{matrix}
\right ]
=
\left[
\begin{matrix}
A_0 \\
A_1 \\
A_2 \\
\vdots \\
A_{n-1}
\end{matrix}
\right ]
\]

​

\(2.IDFT\)

​ 为了方便表示\(,​\) 不妨设：

\[V=
\left [
\begin{matrix}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & \cdots & (\omega_n^0)^{n-1} \\
(\omega_n^1)^0 & (\omega_n^1)^1 & (\omega_n^1)^2 & \cdots & (\omega_n^1)^{n-1} \\
(\omega_n^2)^0 & (\omega_n^2)^1 & (\omega_n^2)^2 & \cdots & (\omega_n^2)^{n-1} \\
\vdots & \vdots & \vdots& \ddots& \vdots\\
(\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & (\omega_n^{n-1})^2 & \cdots & (\omega_n^{n-1})^{n-1} \\
\end {matrix}
\right ]
\\
D=
\left [
\begin{matrix}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & \cdots & (\omega_n^0)^{n-1} \\
(\omega_n^{-1})^0 & (\omega_n^{-1})^1 & (\omega_n^{-1})^2 & \cdots & (\omega_n^{-1})^{n-1} \\
(\omega_n^{-2})^0 & (\omega_n^{-2})^1 & (\omega_n^{-2})^2 & \cdots & (\omega_n^{-2})^{n-1} \\
\vdots & \vdots & \vdots& \ddots& \vdots\\
(\omega_n^{-(n-1)})^0 & (\omega_n^{-(n-1)})^1 & (\omega_n^{-(n-1)})^2 & \cdots & (\omega_n^{-(n-1)})^{n-1} \\
\end {matrix}
\right ]
\\
\]

再回顾一下IDFT要解决的问题\(,\) 已知点值表达\(,\) 求系数表达\(,\) 即\(:\) 已知 \(A\) 求 \(a\)

根据DFT的过程\(,\) 显然可以得到\(:\) \(V \cdot a=A\)

问题就转化为 \(a=V^{-1} \cdot A\)

​

​ 接下来开始填鸭\(:\)

​ (1) 已知一个复数 \(z=a+bi\) \(,\) 则它的共轭复数为 \(z'=a-bi\) \(,\) 显然 $ z \cdot z'=a^2+b2,$

​ 且 \(\omega_n^k\) 的共轭复数为 \(\omega_n^{-k}\) (可以考虑单位根的几何意义)\(;\)

​ 不难发现 \(D\) 中的每个数都是 \(V\) 中对应位置上的共轭复数\(;​\)

​ \(D\) 即为 \(V\) 的共轭矩阵；

​ (2) 两个共轭复数相乘是一个实数，可以尝试性地写出 \(E=V \cdot D ;\)

\[E=
\left [
\begin{matrix}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & \cdots & (\omega_n^0)^{n-1} \\
(\omega_n^1)^0 & (\omega_n^1)^1 & (\omega_n^1)^2 & \cdots & (\omega_n^1)^{n-1} \\
(\omega_n^2)^0 & (\omega_n^2)^1 & (\omega_n^2)^2 & \cdots & (\omega_n^2)^{n-1} \\
\vdots & \vdots & \vdots& \ddots& \vdots\\
(\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & (\omega_n^{n-1})^2 & \cdots & (\omega_n^{n-1})^{n-1} \\
\end {matrix}
\right ]
\left [
\begin{matrix}
(\omega_n^0)^0 & (\omega_n^0)^1 & (\omega_n^0)^2 & \cdots & (\omega_n^0)^{n-1} \\
(\omega_n^{-1})^0 & (\omega_n^{-1})^1 & (\omega_n^{-1})^2 & \cdots & (\omega_n^{-1})^{n-1} \\
(\omega_n^{-2})^0 & (\omega_n^{-2})^1 & (\omega_n^{-2})^2 & \cdots & (\omega_n^{-2})^{n-1} \\
\vdots & \vdots & \vdots& \ddots& \vdots\\
(\omega_n^{-(n-1)})^0 & (\omega_n^{-(n-1)})^1 & (\omega_n^{-(n-1)})^2 & \cdots & (\omega_n^{-(n-1)})^{n-1} \\
\end {matrix}
\right ]
\\
\]

​ 当 \(i=j\) 时\(,\) \(e_{i,j}=\sum_{k=0}^{n-1}v_{i,k} \cdot d_{k,j}=\sum_{k=0}^{n-1} (\omega_n^{i-j})^k=n\)

​ 当 $ i \ne j ​$ 时\(,​\) \(e_{i,j}=\sum_{k=0}^{n-1}v_{i,k} \cdot d_{k,j}=\sum_{k=0}^{n-1}(\omega_n^{(i-j)})^k,​\) 不难发现这是个等比数列\(,​\) 所以\(:​\)​

​ \(e_{i,j}=\frac{\omega_n^{(i-j)n}-1} {\omega_n ^ {i-j} - 1}=0​\)

​ 综上\(,\) \(E\)是一个$n \times n $ 的矩阵\(:\)

\[E=
\left [
\begin{matrix}
n & 0 & 0 & 0 &\cdots& 0 & 0 \\
0 & n & 0 & 0 &\cdots& 0 & 0 \\
0 & 0 & n & 0 &\cdots& 0 & 0 \\
0 & 0 & 0 & n &\cdots& 0 & 0 \\
\vdots & \vdots & \vdots & \vdots &\ddots &\vdots &\vdots \\
0 & 0 & 0 & 0 &\cdots& n & 0 \\
0 & 0 & 0 & 0 &\cdots& 0 & n \\
\end{matrix}
\right]
\]

​ 线性代数中\(,\) 矩阵主对角线上的数都是 \(n\) 的矩阵可以看成是数 \(n,\) 这个可以通过矩阵乘法验证\(,\) 不再赘述\(;\)

​

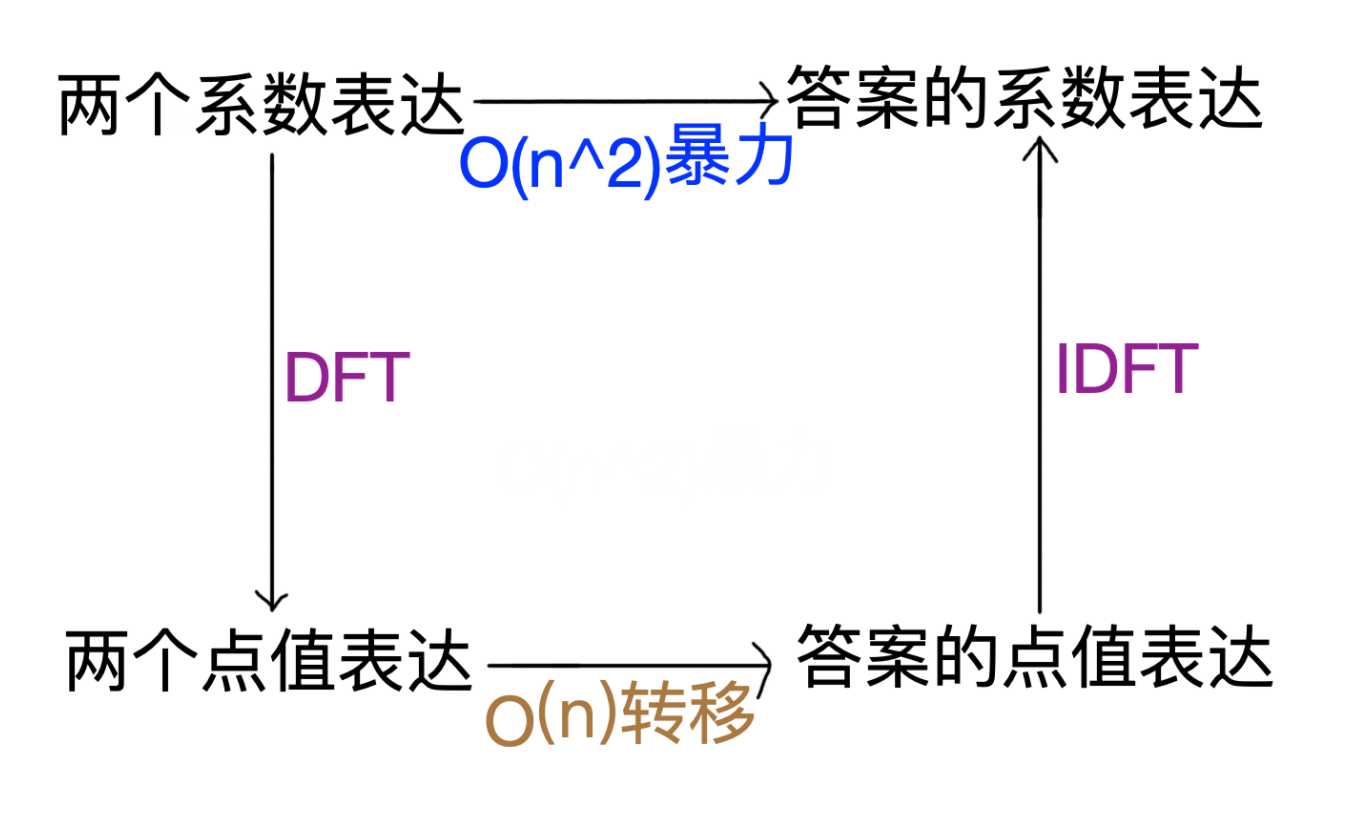
​ 至此\(,\) 求多项式卷积的复杂度仍然是 \(O(n^2),\) 后面的内容就是加速的方法，这里附一张图方便理解\(:\)

四、FFT的实现

​ \(p.s.\) 这里默认 \(n=2^k, k \in Z\)

​ 关于单位根的一些性质\(:\)

​ 1.消去引理 \(\omega_{dn}^{dk}=e^{\frac{2 \pi idk}{dn}}=e^{\frac{2 \pi ik}{n}}=\omega_n^k\)

​ 2.折半引理 \(\omega_n^{k+ \frac{n}{2}}=-\omega_n^k​\)

​ \(prf:\) \(\because \omega_n^n=1\)

​ \(\therefore \omega_n^{\frac{n}{2}} = \pm 1\)

​ 又 \(\because \omega_n^{\frac{n}{2}} \ne \omega_n^n\)

​ \(\therefore \omega_n^{\frac{n}{2}}=-1\)

​ \(\therefore \omega_n^{k+ \frac{n}{2}}=-\omega_n^k\)

​ 设 \(A_0(x)=a_0x^0+a_2x+a_4x^2+ \cdots +a_{n-2}x^{\frac{n}2-1},​\) \(A_1(x)=a_1x^0+a_3x^1+a_5x^2+ \cdots +a_{n-1}x^{\frac{n}2-1}​\)

​ 则 \(A(x)=A_0(x^2)+xA_1(x^2);​\)

​ 把 \(x=\omega_n^k\) 代入\(,\) 根据消去引理可得\(:\) \((\omega_n^k)^2 = \omega_{\frac{n}{2}}^k\)

​ 所以柿子可以写成\(:\)

\[A(\omega_n^k)=A_0(\omega_{\frac{n}{2}}^k)+\omega_n^k(A_1(\omega_{\frac{n}{2}}^k) \\
A(\omega_n^{k+\frac{n}{2}})=A_0(\omega_{\frac{n}{2}}^k)-\omega_n^k(A_1(\omega_{\frac{n}{2}}^k)\\
\]

​ 直接递归实现就好了\(,\) 和之前说的一样\(,\) 要把 \(n\) 补齐 \(2\) 的次幂\(,\) 代码如下\(;\)

​ \(p.s.\) 有个小的常数优化 \(——\) 复数手写\(,\) 不用 \(stl\)

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef double db;
typedef long long ll;
inline int in() {
    int x=0;char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x;
}
template<typename T>
inline void out(T x) {
    int cnt=0;
    static char s[20];
    do s[cnt++]=x%10; while(x/=10);
    while(cnt--) putchar(s[cnt]+48);
    putchar(' ');
}

const int N = (int)3e6+5;
const db PI=acos(-1);
struct cp {
    db real, imag;
    cp(db x=0, db y=0) { this->real=x, this->imag=y; }
    inline cp operator + (const cp x) { return cp(this->real+x.real, this->imag+x.imag); }
    inline cp operator - (const cp x) { return cp(this->real-x.real, this->imag-x.imag); }
    inline cp operator * (const cp x) {
        return cp(this->real*x.real-this->imag*x.imag, this->real*x.imag+this->imag*x.real);
    }
};
cp x[N], y[N];
int n, m, nn;

void fft(int n, cp *a, int k) {
    if(n==1) return ;
    int nn=n>>1;
    cp a0[nn+1], a1[nn+1];
    for(int i=0;i<nn;i++) a0[i]=a[i<<1], a1[i]=a[i<<1|1];
    fft(nn, a0, k); fft(nn, a1, k);
    cp omega_n(cos(2*PI/n), sin(k*2*PI/n)), omega(1, 0);
    for(int i=0;i<nn;i++) {
        a[i]=a0[i]+omega*a1[i];
        a[i+nn]=a0[i]-omega*a1[i];
        omega=omega*omega_n;
    }
}

int main() {
    n=in(), m=in();
    for(int i=0;i<=n;i++) x[i].real=in();
    for(int i=0;i<=m;i++) y[i].real=in();
    m+=n, nn=1;
    while(nn<=m) nn<<=1;
    fft(nn, x, 1); fft(nn, y, 1);
    for(int i=0;i<nn;i++) x[i]=x[i]*y[i];
    fft(nn, x, -1);
    for(int i=0;i<=m;i++) out((int)(x[i].real/nn+0.5));
    putchar('\n');
    return 0;
}

五、迭代实现

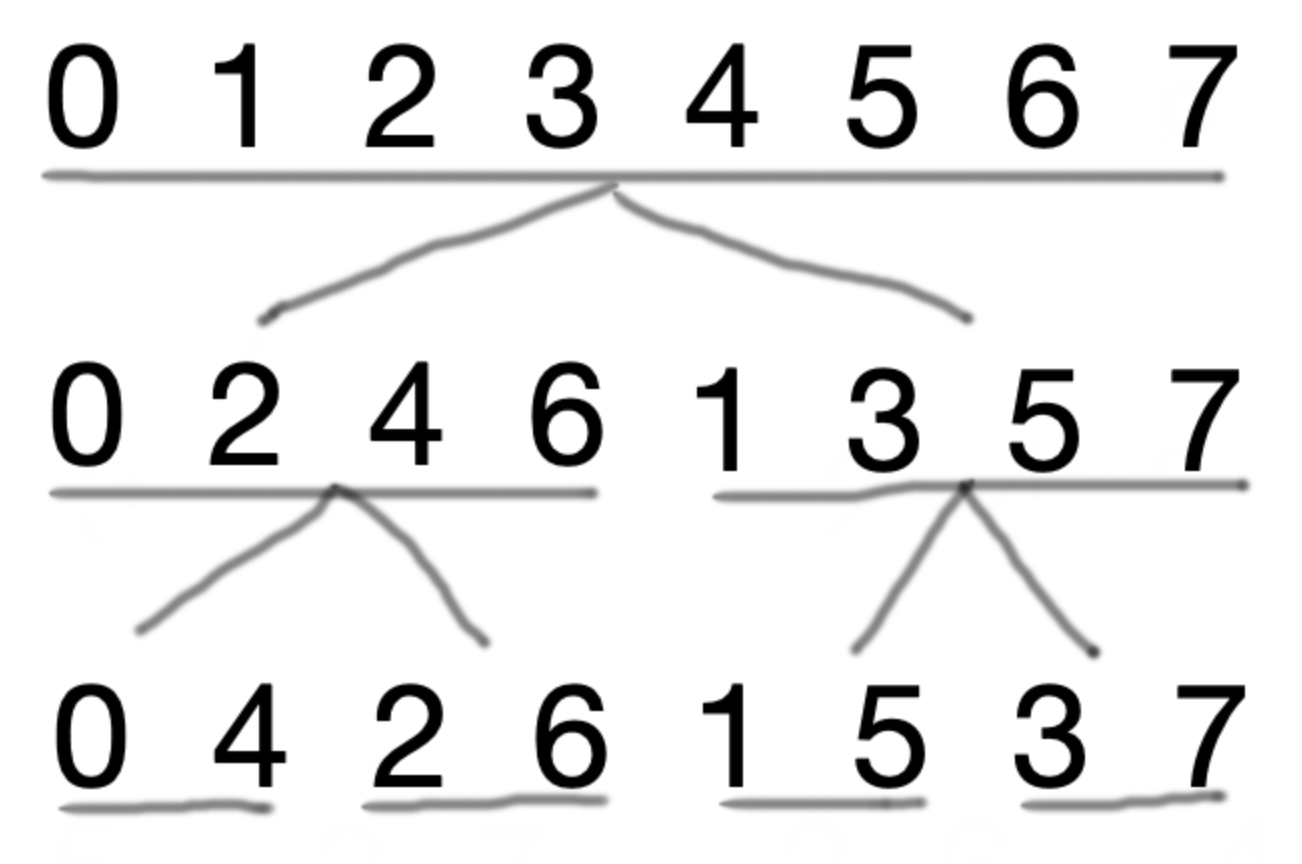
​ 在递归实现时\(,\) 把当前的 \(A\) 奇偶分组\(,\) 实际上是按末尾二进制位分组\(,\) 不妨考虑 \([0, n-1]\) 的二进制\(;\)

​ 每次递归分组时\(,\) 显然二进制是从最低位到最高位产生影响\(,\) 可以得到如下结论\(:\)

​ \(A\) 中的每个数在递归终止时所在的位置的编号\(,\) 就是把它开始所在位置二进制反过来得到的\(;\)

​ 简单验证一下:

Before	-	-	End
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

​ 那么问题来了\(,\) 代码怎么实现》》》

​ \(rev_i=rev_{i/2}/2+(i\) \(mod\) \(2)*(\frac{n}{2})\)

​ 把 \(i\) 右移一位\(,\) 反过来\(,\) 再把之前在开头的 \(0\) 移走\(,\) 再把最后一位的贡献计算出来即可\(;\)

​ 上代码 \(:\)

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef double db;
typedef long long ll;
inline int in() {
    int x=0;char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x;
}
template<typename T>
inline void out(T x) {
    int cnt=0;
    static char s[20];
    do s[cnt++]=x%10; while(x/=10);
    while(cnt--) putchar(s[cnt]+48);
    putchar(' ');
}

const int N = (int)3e6+5;
const db PI=acos(-1);
struct cp {
    db real, imag;
    cp(db x=0, db y=0) { this->real=x, this->imag=y; }
    inline cp operator + (const cp x) { return cp(this->real+x.real, this->imag+x.imag); }
    inline cp operator - (const cp x) { return cp(this->real-x.real, this->imag-x.imag); }
    inline cp operator * (const cp x) {
        return cp(this->real*x.real-this->imag*x.imag, this->real*x.imag+this->imag*x.real);
    }
};
cp x[N], y[N];
int n, m, nn, rev[N];

inline void fft(const int n, cp *a, const int k) {
    for(int i=1;i<=n;i++) if(i<rev[i]) std::swap(a[i], a[rev[i]]);

    for(int len=2;len<=n;len<<=1) {
        cp omega_n(cos(2*PI/len), sin(2*PI*k/len));
        int m=len>>1;
        for(int i=0;i<n;i+=len) {
            cp omega(1, 0);
            for(int j=i;j<i+m;j++) {
                cp t1=a[j], t2=omega*a[j+m];
                a[j]=t1+t2, a[j+m]=t1-t2;
                omega=omega*omega_n;
            }
        }
    }

    if(k==-1)
        for(int i=0;i<n;i++) a[i].real=(int)(a[i].real/n+0.5);
}

int main() {
    n=in(), m=in();
    for(int i=0;i<=n;i++) x[i].real=in();
    for(int i=0;i<=m;i++) y[i].real=in();
    m+=n, nn=1;
    while(nn<=m) nn<<=1;
    for(int i=1;i<nn;i++) rev[i]=(rev[i>>1]>>1)|(i&1)*(nn>>1);

    fft(nn, x, 1); fft(nn, y, 1);
    for(int i=0;i<nn;i++) x[i]=x[i]*y[i];
    fft(nn, x, -1);
    for(int i=0;i<=m;i++) out((int)(x[i].real));
    putchar('\n');
    return 0;
}