C# 堆栈（Stack）和队列（Queue）

一、什么是堆？（Heap）

     堆是无序的，是一片不连续的内存域，由用户自己来控制和释放，如果用户自己不释放的话，当内存达到一定的特定值时，通过垃圾回收器（GC）来回收。

     是程序运行期间动态分配的内存空间，你可以根据程序的运行情况确定要分配的堆内存的大小。

二、什么是栈？（Stack）

     栈是有顺序的，是一片连续的内存域，保持着先进后出的原则，由系统自动分配和维护。

     是编译期间就分配好的内存空间，因此代码中必须就栈的大小有明确的定义。

     表尾允许进行插入删除操作，称为栈顶（Top），另一端是固定的，称为栈底（Bottom）。

     PS：

     线性表（Linear List）是具有相同特性的数据元素的一个有限序列。

     堆栈（Stack） 是一种特殊的线性表，是一种操作只允许在尾端进行插入或删除等操作的线性表。

     顺序栈（Sequence Stack）是用一片连续的存储空间来存储栈中的数据元素。

     链栈（Linked Stack）是用链式存储结构来存储的栈，链栈通常用单链表来表示。

三、什么是堆栈？

     由堆和栈的概念，可以清晰的知道，堆栈是一种数据项按序排列的数据结构，只能在一端称为栈顶（top）对数据项进行插入和删除。

     最后一个放入堆栈中的物体总是被最先拿出来，这个特性通常称为后进先出（LIFO）队列。

     堆栈中定义了一些操作，两个最重要的是PUSH和POP。PUSH操作在堆栈的顶部加入一个元素，POP操作相反，在堆栈顶部移去一个元素， 并将堆栈的大小减一。

     PS：通常所说的堆栈，实际上更偏向于指栈。

四、什么是队列？（Queue）

     队列是一种特殊的线性表，它只允许在表的前端（Front）进行删除操作，而在表的后端（Rear）进行插入操作。

     进行插入操作的表尾称为队尾（Rear），把进行其他操作的头部称为队头（Front）。

     队列中没有元素时，称为空队列，队列具有先进先出（FIFO）的特点。

     PS：

     队列（Queue）是插入操作限定在表的尾部而其他操作限定在表的头部进行的线性表。

     顺序队列（Sequence Queue）用一片连续的存储空间来存储队列中的数据元素，类似于顺序表，用一维数组来存放队列中的数据元素。

     循环顺序队列（Circular sequence Queue）解决顺序队列的假溢出的方法是将顺序队列看成是首位相接的循环结构。

     链队列（Linked Queue）队列的另外一种存储方式是链式存储，通常用单链表表示。

五、堆、栈之间的区别是?

     堆实际上指的就是（满足堆性质的）优先队列的一种数据结构，第一个元素有最高的优先权

     栈实际上就是满足先进后出的性质的数学或数据结构。

     1、堆栈空间分配

     栈（操作系统）：由操作系统自动分配释放 ，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中的栈。

     堆（操作系统）：一般由程序员分配释放， 若程序员不释放，程序结束时可能由OS回收，分配方式倒是类似于链表。

     2、堆栈缓存方式

     栈使用的是一级缓存， 他们通常都是被调用时处于存储空间中，调用完毕立即释放。

     堆则是存放在二级缓存中，生命周期由虚拟机的垃圾回收算法来决定（并不是一旦成为孤儿对象就能被回收）。所以调用这些对象的速度要相对来得低一些。

     3、堆栈数据结构区别

     堆（数据结构）：堆可以被看成是一棵树，如：堆排序。

     栈（数据结构）：一种先进后出的数据结构。

     特性： 最后一个放入堆栈中的物体总是被最先拿出来， 这个特性通常称为后进先出(LIFO)队列。

六、堆、栈、队列之间的区别是？

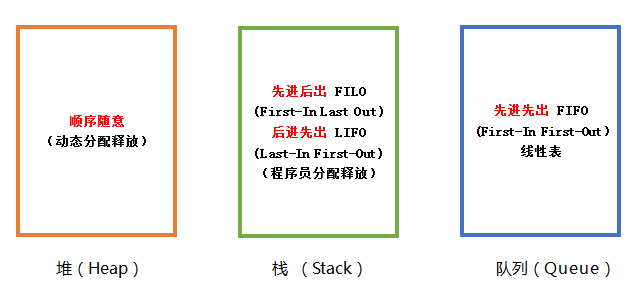
     堆是在程序运行时，而不是在程序编译时，申请某个大小的内存空间。即动态分配内存，对其访问和对一般内存的访问没有区别。

     栈就是一个桶，后放进去的先拿出来，它下面本来有的东西要等它出来之后才能出来。（先进后出or后进先出）

     队列只能在队头做删除操作,在队尾做插入操作.而栈只能在栈顶做插入和删除操作。（先进先出）