The Problem of Overfitting

Cost Function

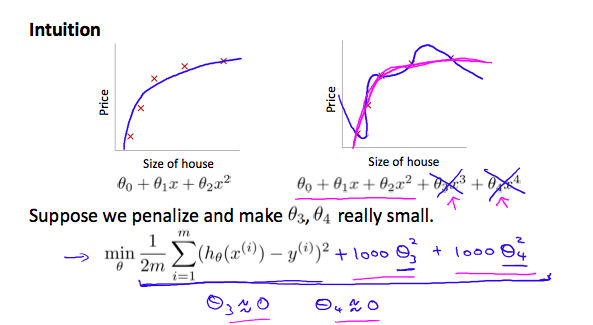
Regularized Linear Regression

Note: [8:43 - It is said that X is non-invertible if m ≤ n. The correct statement should be that X is non-invertible if m < n, and may be non-invertible if m = n.

We can apply regularization to both linear regression and logistic regression. We will approach linear regression first.

Regularized Logistic Regression

We can regularize logistic regression in a similar way that we regularize linear regression. As a result, we can avoid overfitting. The following image shows how the regularized function, displayed by the pink line, is less likely to overfit than the non-regularized function represented by the blue line:

Solving the Problem of Overfitting的更多相关文章

  1. machine learning(13) -- solving the problem of overfitting:regularization

    solving the problem of overfitting:regularization 发生的在linear regression上面的overfitting问题 发生在logistic ...

  2. 机器学习(四)正则化与过拟合问题 Regularization / The Problem of Overfitting

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...

  3. The first step in solving any problem is recognizing there is one.

    The first step in solving any problem is recognizing there is one.解决问题的第一步是要承认确实存在问题.

  4. 吴恩达机器学习笔记19-过拟合的问题（The Problem of Overfitting）

    到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合(over-fitting)的问题,可能会导致 ...

  5. 1763 An Essay towards solving a Problem in the Doctrine of Chances

    https://en.wikipedia.org/wiki/An_Essay_towards_solving_a_Problem_in_the_Doctrine_of_Chances

  6. Ng第七课：正则化与过拟合问题 Regularization/The Problem of Overfitting

    7.1  过拟合的问题 7.2  代价函数 7.3  正则化线性回归 7.4  正则化的逻辑回归模型 7.1  过拟合的问题 如果我们有非常多的特征,我们通过学习得到的假设预测可能能够非常好地适应训练 ...

  7. Machine Learning - 第3周（Logistic Regression、Regularization）

    Logistic regression is a method for classifying data into discrete outcomes. For example, we might u ...

  8. 《Machine Learning》系列学习笔记之第三周

    第三周 第一部分 Classification and Representation Classification 为了尝试分类,一种方法是使用线性回归,并将大于0.5的所有预测映射为1,所有小于0. ...

  9. Andrew Ng机器学习课程笔记--week3（逻辑回归&正则化参数）

    Logistic Regression 一.内容概要 Classification and Representation Classification Hypothesis Representatio ...

随机推荐

  1. python 数字计算模块 decimal（小数计算）

    from decimal import * a = Decimal('0.1')+Decimal('0.1')+Decimal('0.1')+Decimal('0.3') float(a) >& ...

  2. python爬虫之『入门基础』

    HTTP请求 1.首先需要了解一下http请求,当用户在地址栏中输入网址,发送网络请求的过程是什么? 可以参考我之前学习的时候转载的一篇文章一次完整的HTTP事务过程–超详细 2.还需要了解一下htt ...

  3. Python day字符串所有使用

    字符串所有的操作name = "dio"names = "my\t name is {Name} and i am a {job}"print(name.cap ...

  4. python学习日记-180823

    列表 a=[ ] 1.负数下标:a=[-1]指的是列表a最后一个下标,-2指倒数第二个下标 2.切片——利用切片获得子列表 a[1:4]——'1'切片开始处的下标,‘4’切片结束处的下标(不包括此下标 ...

  5. 今日题解------uvalive 2689

    今天学到了代码以外的东西,就是你在vj上挂了content ,然后你想更新它,你就要刷新一下,不然你提交的那题可能提交到别的地方. 好了回到重点,本题的题意是: #include<bits/st ...

  6. Perl OOP

    1. 模块/类(包) 创建一个名为Apple.pm的包文件(扩展名pm是包的缺省扩展名.意为Perl Module). 一个模块就是一个类(包). 2. new方法 new()方法是创建对象时必须被调 ...

  7. iOS - 系统经常使用框架(framework)的简介

    系统框架(framework)的简介 ImageIO  - 该框架的接口可用于导入或导出图像数据及图像元数据 CoreTelephony  - 获取IMSI号,SIM卡背面的号码是SIM卡的电子串号, ...

  8. [NowCoder]牛客网NOIP赛前集训营-提高组（第七场）

    链接 A.中国式家长2 模拟题,毫无坑点 #include<bits/stdc++.h> #define REP(i,a,b) for(int i(a);i<=(b);++i) #d ...

  9. Arrays.asList()方法的限制

    Arrays.asList()方法的限制是他对所产生的List类型做出了最理想的假设 package example; import java.util.Arrays; import java.uti ...

  10. while 循环的理解

    if 与 while 的主要区别:if 只判断和执行一次,而 while 却代表着一个循环,执行多少次,要视情况而定: 两种情况(A.B)都会让循环体执行: while A or B: 两种情况(A. ...