逻辑回归模型（Logistic Regression）及Python实现

逻辑回归模型（Logistic Regression）及Python实现

http://www.cnblogs.com/sumai

1.模型

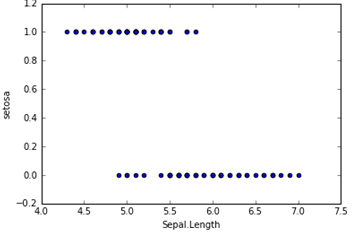
　　在分类问题中，比如判断邮件是否为垃圾邮件，判断肿瘤是否为阳性，目标变量是离散的，只有两种取值，通常会编码为0和1。假设我们有一个特征X，画出散点图，结果如下所示。这时候如果我们用线性回归去拟合一条直线：h_θ(X) = θ₀+θ₁X，若Y≥0.5则判断为1，否则为0。这样我们也可以构建出一个模型去进行分类，但是会存在很多的缺点，比如稳健性差、准确率低。而逻辑回归对于这样的问题会更加合适。

　　逻辑回归假设函数如下，它对θ^TX作了一个函数g变换，映射至0到1的范围之内，而函数g称为sigmoid function或者logistic function，函数图像如下图所示。当我们输入特征，得到的h_θ(x)其实是这个样本属于1这个分类的概率值。也就是说，逻辑回归是用来得到样本属于某个分类的概率。

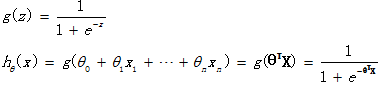
2.评价

回想起之前线性回归中所用到的损失函数：

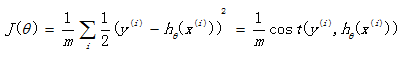
　如果在逻辑回归中也运用这种损失函数，得到的函数J是一个非凸函数，存在多个局部最小值，很难进行求解，因此需要换一个cost函数。重新定义个cost函数如下：

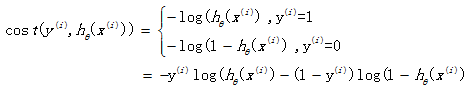
当实际样本属于1类别时，如果预测概率也为1，那么损失为0，预测正确。相反，如果预测为0，那么损失将是无穷大。这样构造的损失函数是合理的，并且它还是一个凸函数，十分方便求得参数θ，使得损失函数J达到最小。

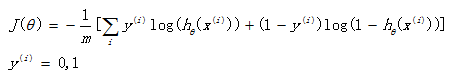
3.优化

我们已经定义好了损失函数J(θ)，接下来的任务就是求出参数θ。我们的目标很明确，就是找到一组θ，使得我们的损失函数J(θ)最小。最常用的求解方法有两种：批量梯度下降法(batch gradient descent)， 牛顿迭代方法((Newton's method)。两种方法都是通过迭代求得的数值解，但是牛顿迭代方法的收敛速度更加快。

批量梯度下降法：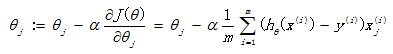 

牛顿迭代方法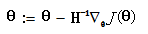：  (H为海瑟矩阵)

4.python代码实现

 # -*- coding: utf-8 -*-
 """
 Created on Wed Feb 24 11:04:11 2016

 @author: SumaiWong
 """

 import numpy as np
 import pandas as pd
 from numpy import dot
 from numpy.linalg import inv

 iris = pd.read_csv('D:\iris.csv')
 dummy = pd.get_dummies(iris['Species']) # 对Species生成哑变量
 iris = pd.concat([iris, dummy], axis =1 )
 iris = iris.iloc[0:100, :] # 截取前一百行样本

 # 构建Logistic Regression , 对Species是否为setosa进行分类 setosa ~ Sepal.Length
 # Y = g(BX) = 1/(1+exp(-BX))
 def logit(x):
     return 1./(1+np.exp(-x))

 temp = pd.DataFrame(iris.iloc[:, 0])
 temp['x0'] = 1.
 X = temp.iloc[:,[1,0]]
 Y = iris['setosa'].reshape(len(iris), 1) #整理出X矩阵 和 Y矩阵

 # 批量梯度下降法
 m,n = X.shape #矩阵大小
 alpha = 0.0065 #设定学习速率
 theta_g = np.zeros((n,1)) #初始化参数
 maxCycles = 3000 #迭代次数
 J = pd.Series(np.arange(maxCycles, dtype = float)) #损失函数

 for i in range(maxCycles):
     h = logit(dot(X, theta_g)) #估计值
     J[i] = -(1/100.)*np.sum(Y*np.log(h)+(1-Y)*np.log(1-h)) #计算损失函数值
     error = h - Y #误差
     grad = dot(X.T, error) #梯度
     theta_g -= alpha * grad
 print theta_g
 print J.plot()   

 # 牛顿方法
 theta_n = np.zeros((n,1)) #初始化参数
 maxCycles = 10 #迭代次数
 C = pd.Series(np.arange(maxCycles, dtype = float)) #损失函数
 for i in range(maxCycles):
     h = logit(dot(X, theta_n)) #估计值
     C[i] = -(1/100.)*np.sum(Y*np.log(h)+(1-Y)*np.log(1-h)) #计算损失函数值
     error = h - Y #误差
     grad = dot(X.T, error) #梯度
     A =  h*(1-h)* np.eye(len(X))
     H = np.mat(X.T)* A * np.mat(X) #海瑟矩阵, H = X`AX
     theta_n -= inv(H)*grad
 print theta_n
 print C.plot()   

代码所用的数据下载地址：http://files.cnblogs.com/files/sumai/iris.rar