[JZOJ 5906] [NOIP2018模拟10.15] 传送门 解题报告（树形DP）

题目链接：

https://jzoj.net/senior/#contest/show/2528/2

题目：

8102年，Normalgod在GLaDOS的帮助下，研制出了传送枪。但GLaDOS想把传送枪据为己有，于是把Normalgod扔进了一间实验室。这间实验室是一棵有n个节点的树。现在Normalgod在一号节点，出口也在一号节点，但为了打开它，必须经过每一个节点按下每个节点的开关，出口才能打开。GLaDOS为了杀死Normalgod，开始在实验室里释放毒气，因此Normalgod必须尽快逃出这间实验室。
 当然，Normalgod手中的传送枪是可以使用的。传送枪可以发射出两个颜色不同的传送门。Normalgod可以从其中一个传送到另一个。尽管传送枪可以在视野范围内的任何一个经过特殊处理的表面打开一扇传送门，但这间实验室的设计使得Normalgod只能在他所处的房间内打开一个传送门。 在已经存在了一个同颜色的传送门时，打开新的传送门会使与它同颜色的旧门消失。传送和打开传送门所需时间为0。
显然，利用传送枪会让Normalgod更快解决谜题，可Normalgod死在了按下最后一个按钮的路上。尽管如此，GLaDOS还是很想知道到底Normalgod最快能用多久逃出去，这对她的实验室设计方法论有重要的指导作用。作为GLaDOS的算法模块，你要完成这个任务。本题时限为2000ms

题解：

（声明：题解来自JZOJ）

1.易知：每条边至多经过2次。

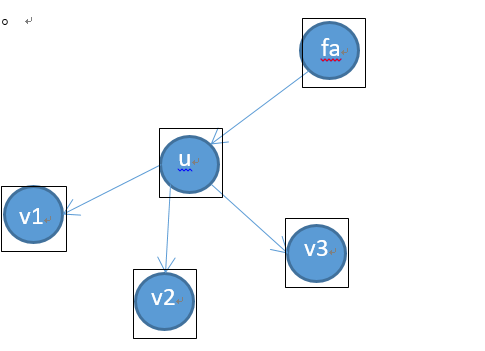
如图：若将传送门置于fa处，则fa->u经过3次；

实际上若将传送门置于u处，则fa->u经过2次，更优。

2.那么最长距离总权值*2，那么我们只需要使经过一次的边的总和更大，

则长度=总权值*2-选用的单边权值之和。

3.由此我们可以采用动态规划来求解。

dp[i][0/1]

0表示在i点及i点儿子设传送门所能得到的最大总和

1 表示不在i点及i点儿子设传送门所能得到的最大总和

首先，对于dp[i][1]的情况，一定存在i点的祖先中有传送门，这样才能使结果更优。所以对于他的每一个儿子都能跳回到他的祖先。但实际上只有使一个儿子跳回祖先时，才能保证fa->i的边经过两次。

否则转化为dp[i][0]的情况。则我们要使选的儿子最优。

$dp[i][1]=max(dp[vi][1]+wi)$

其次，对于dp[i][0]的情况，在每个儿子中设立传送门并不会影响到其他儿子，因为总能从儿子回到i时再在i重设传送门。所以我们就取每个儿子设与不设的最优值之和。

$dp[i][0]=max(dp[vi][0],dp[vi][1]+wi)$

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;

const int N=1e6+;
int n,tot;
int head[N];
ll ans;
ll dp[N][];
struct EDGE
{
    int to,nxt;
    ll w;
}edge[N<<];
inline ll read()
{
    char ch=getchar();
    int s=,f=;
    while (ch<''||ch>'') {if (ch=='-') f=-;ch=getchar();}
    while (ch>=''&&ch<='') {s=(s<<)+(s<<)+ch-'';ch=getchar();}
    return s*f;
}
void add(int u,int v,ll w)
{
    edge[++tot]=(EDGE){v,head[u],w};
    head[u]=tot;
}
void dfs(int x,int pre)
{
    for (int i=head[x];i;i=edge[i].nxt)
    {
        int y=edge[i].to;
        if (y==pre) continue;
        dfs(y,x);
        dp[x][]=max(dp[x][],dp[y][]+edge[i].w);//不设传送门
        dp[x][]+=max(dp[y][],dp[y][]+edge[i].w);//设传送门
    }
}
int main()
{
    freopen("portal.in","r",stdin);
    freopen("portal.out","w",stdout);
    n=read();
    ll w;
    for (int i=,u,v;i<n;i++)
    {
        u=read();v=read();w=read();
        add(u,v,w);add(v,u,w);ans+=w<<;
    }
    dfs(,-);
    ans-=max(dp[][],dp[][]);
    printf("%lld\n",ans);
    return ;
}