网络流入门——EK算法

转载：https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html

网络流的相关定义：

• 源点：有n个点，有m条有向边，有一个点很特殊，只出不进，叫做源点。
• 汇点：另一个点也很特殊，只进不出，叫做汇点。
• 容量和流量：每条有向边上有两个量，容量和流量，从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].

通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有“进入”他们的流量和等于所有从他本身“出去”的流量。

• 最大流：把源点比作工厂的话，问题就是求从工厂最大可以发出多少货物，是不至于超过道路的容量限制，也就是，最大流。

求解思路：

首先，假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。

一个最简单的例子就是，零流，即所有的流量都是0的流。

• (1).我们就从这个零流开始考虑，假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。
• (2).那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的。
• (3).这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。
• (4).当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。

补充：

• (1).寻找增广路的时候我们可以简单的从源点开始做BFS，并不断修改这条路上的delta 量，直到找到源点或者找不到增广路。
• (2).在程序实现的时候，我们通常只是用一个c 数组来记录容量，而不记录流量，当流量+delta 的时候，我们可以通过容量-delta 来实现，以方便程序的实现。

相关问题：

为什么要增加反向边？

在做增广路时可能会阻塞后面的增广路，或者说，做增广路本来是有个顺序才能找完最大流的。

但我们是任意找的，为了修正，就每次将流量加在了反向弧上，让后面的流能够进行自我调整。

举例：

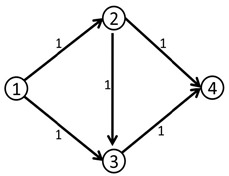
比如说下面这个网络流模型

我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。

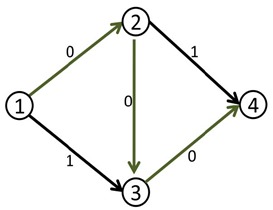
于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但是，

这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？

问题就在于我们没有给程序一个“后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。

那么如何解决这个问题呢？

我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。

           c[x,y]-=delta;

           c[y,x]+=delta;

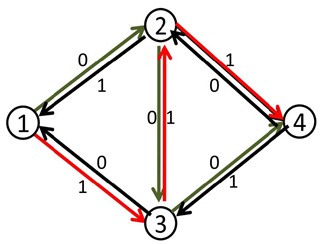
我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下：

这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

那么，这么做为什么会是对的呢？

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给“退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。

如果这里没有2-4怎么办？

这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点

同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流。

附录：(edmonds-Karp版本)

   1:  void update_residual_network(int u,int flow){                                             

   2:      while(pre[u]!=-1){

   3:          map[pre[u]][u]-=flow;                   

   4:          map[u][pre[u]]+=flow;                  

   5:          u=pre[u];

   6:      }

   7:  }

   8:  int find_path_bfs(int s,int t){

   9:      memset(visited,0,sizeof(visited)); 

  10:      memset(pre,-1,sizeof(pre));

  11:      visited[s]=1;

  12:      int min=INF;

  13:      queue<int> q;

  14:      q.push(s);

  15:   

  16:      while(!q.empty()){

  17:          int cur=q.front();q.pop();

  18:          if(cur==t)   break;  

  19:   

  20:          for(int  i = 1 ; i <= m ; i++ ){

  21:              if( visited[i] == 0 && map[cur][i] != 0){

  22:                  q.push(i);

  23:                  min=(min<map[cur][i]?min:map[cur][i]) ;

  24:                  pre[i]=cur;

  25:                  visited[i]=1;

  26:              }

  27:          }

  28:      }

  29:      if(pre[t]==-1) return 0;

  30:      

  31:      return min;

  32:  }

  33:  int edmonds_karp(int s,int t){

  34:      int new_flow=0;

  35:      int max_flow=0;

  36:      do{

  37:          new_flow = find_path_bfs(s,t);

  38:          update_residual_network(t,new_flow);

  39:          max_flow += new_flow;

  40:      }while( new_flow != 0 );

  41:      return max_flow;

  42:  }