[luogu P2586] GCD 解题报告 (莫比乌斯反演|欧拉函数)

题目链接：https://www.luogu.org/problemnew/show/P2568#sub

题目大意：

计算​$\sum_{x=1}^n\sum_{y=1}^n [gcd(x,y)==prime]​$

题解：

解法一：莫比乌斯反演套路题

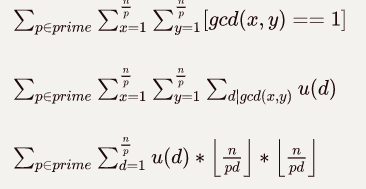
其实这样就可以了，但是还可以优化一下子

设​​T=dp

​

整除分块就好了，其实这就和 yy的gcd 一样了

解法二：欧拉函数

考虑上面的第一个式子​可以化简成

​

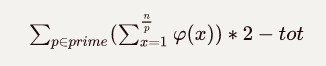
tot是n以内质数的数量

这是因为考虑到每次都两次计算了​$\varphi(1)$

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;

const int N=1e7+;
int n,tot;
ll ans;
int prime[];
ll phi[N];
bool vis[N];
void get_phi()
{
    phi[]=;
    for (int i=;i<=n;i++)
    {
        if (!vis[i]) {phi[i]=i-;prime[++tot]=i;}
        for (int j=;j<=tot&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=;
            if (i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-);
            else
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
        }
    }
    for (int i=;i<=n;i++) phi[i]=phi[i-]+phi[i];
}
int main()
{
    scanf("%d",&n);
    get_phi();
    //for (int i=1;i<=n;i++) printf("%d ",phi[i]);
    for (int i=;i<=tot;i++)
    {
        ans+=phi[n/prime[i]];
    }
    printf("%lld\n",ans*-tot);
    return ;
}