1、Attention_based Group recommendation——基于注意力机制的群组推荐

1、摘要：

本文将Attention-based模型和BPR模型结合对给定的群组进行推荐项目列表。

2、算法思想：

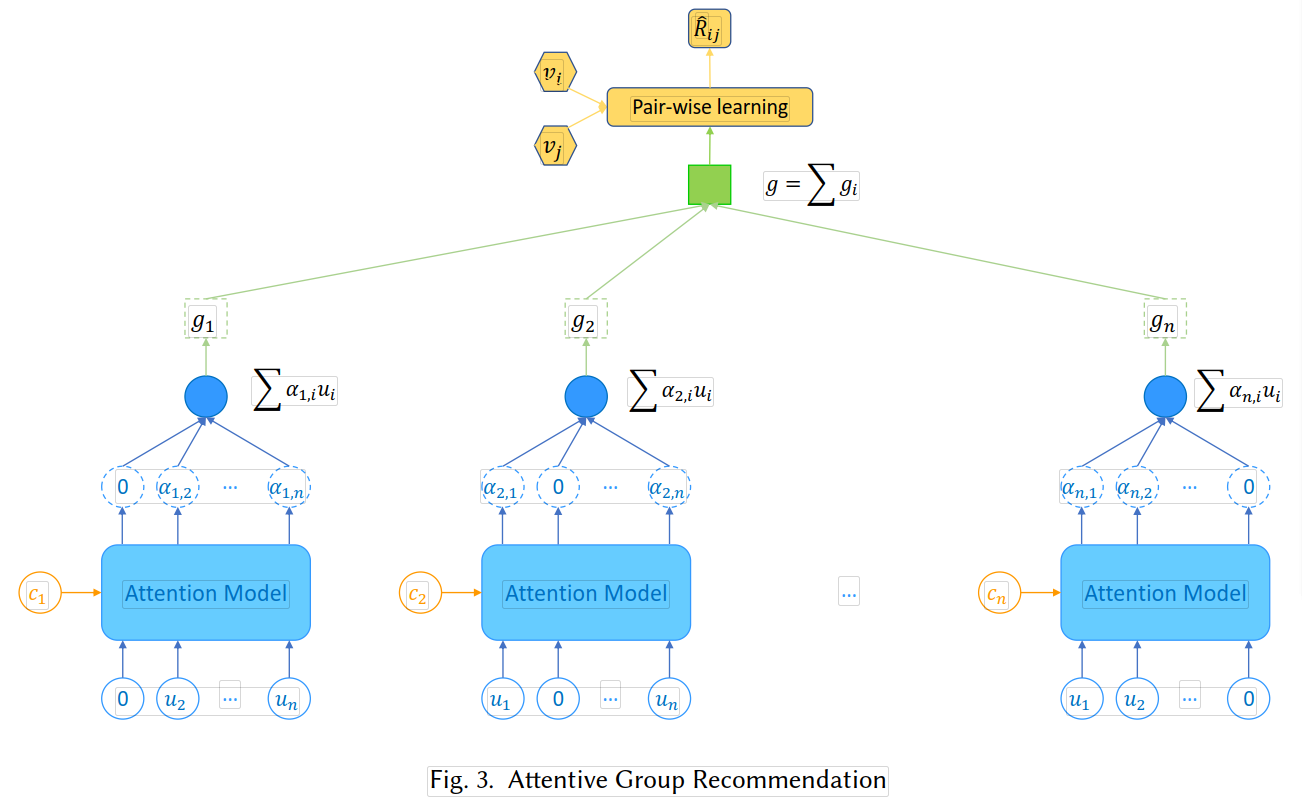
如图：

attention-based model：【以下仅计算一个群组的偏好，多个群组计算过程一样】

① 群组：以上为n个子群组，来自于一个给定的群组，包含用户 { u₁，u₂，u₃，……，u_n }，

② α_i，j：定义α_i，j为用户 j 的子群组 i （不包含用户 i ）的偏好程度。因为 α_i，j作为用户 j 对整个群组的重要程度，而不仅仅是对用户 i 。

③ c _i ：表示用户 i 的上下文向量

可以将以上每个attention模型理解成群组中其他成员 j 分别与用户 i 的相似度，即（α_i，j），得到的 g_i = ∑ α_i，j* u _j 是用户 i 在整个群组中的投票权重。

④ g : g = ∑ g_i, 表示投票方案对所有用户的投票平等的进行计算。

蓝色的Attention model中的函数：（即 ci 和 ui 结合的函数）

对其归一化处理：

然后计算群组的潜在向量：

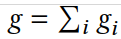
BPR：

传统的BPR是根据单个用户对项目的偏序进行计算用户偏好来个性化推荐。

这里将Attention模型和BPR结合得到的是群组的偏好，即一个群组看成一个用户。

传统的BPR目标函数：

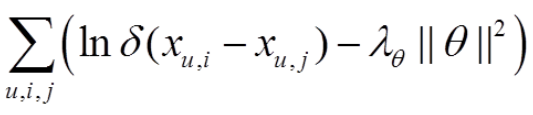
其中，δ 是激活函数，x _u，i 表示用户 u 对项目 i 的偏好程度。x _u，i - x _{u ，j}大于0，因为BPR的输入：三元组（u,i,j)的意思是：用户u 对项目 i 的偏好程度比 j 大。正则化项：θ 是参数，这里的参数矩阵分解：将X分解成 x ₌p* q ,p 和 q 为参数。故可以以上目标函数可以写成：

在本文目标函数：

其中：

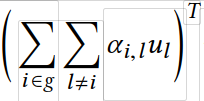为attention得到的最终结果 g^T。

U，C，I：用户潜在向量，用户上下文向量和项目向量的集合。都为参数。

（g , j , k)：属于集合Ds的三元组，包含每个群组的所有正项和负项对。

α_i，l：用户 l 在子群组 i 的权重。

两个模型的总结：

采用attention计算群组的潜在向量，然后利用组的潜在向量作为群组的潜在特征，将群组的潜在特征和项目的潜在特征相乘作为整个群组对项目的偏好程度。如矩阵分解：X= W*H，则 Attention 算出 W，与项目特征H相乘（H是要计算的参数），X就是群组对项目的偏好程度，可以用来做推荐。

3、实验：

（1）数据集：

①来自于基于事件的社交网络 EBSN的数据：Plancast2。由用户组和地点组成。eg：事件A组：事件中每个用户都是组成员。小组成员将选择一个场地（候选项目）来主持比赛。我们的目标是推荐一个团体活动的场地。

②从EBSN Meetup3中爬取的数据。目的也是给一个给定的团体推荐一个举办活动的场所。

③来自于MovieLens 1M Data4，Miviels1m数据包含约一百万部电影评级，来自约6000部用户，约4000部电影。

从MOVILELNS 1M数据中提取两个数据集：Mivieles Simi和Mivieles Rand。当MovieLens-Simi数据中的用户具有较高的内部组相似性时，它们被分配到相同的组中，而MovieLens-Rand数据中的用户被随机分组。

因此，MovieLens-Simi和MovieLens-Rands组类似于两个典型的现实生活情况：组可以包括具有相似偏好的人，也可以包括不相关的人之间的形式。例如，一组亲密的朋友具有较高的内部组相似性，而同一辆车上的人可以被认为是随机组。

（2）评价指标：准确度、召回率、NDCG

（3）六种基线推荐方法：

CF-AVG、CF-LM、CF-RD、PIT、COM、MF-AVG。

CF-AVG、CF-LM、CF-RD是得分聚合方法，PIT和COM是最新的概率模型，MF-AVG是矩阵分解模型。

基于用户的平均策略CF(CF-AVG)：CF-AVG应用基于用户的CF来计算每个用户对候选项i的偏好评分，然后对所有用户的偏好评分进行平均，以获得项i的组推荐评分。
基于用户的最小痛苦策略CF(CF-LM)：与CF-AVG类似，CF-LM首先应用基于用户的CF来计算每个用户关于候选项i的得分。然而，项目i的推荐得分被看作所有用户中项目的最低偏好得分。
基于用户的关联和不同意策略(CF-RD)[3]：CF-RD还执行基于用户的CF来计算每个用户关于候选项i的分数。相关性得分是使用CF-AVG或CF-LM获得的，而分歧得分是项目在组成员之间的平均成对相关性差异（平均成对分歧方法），或项目在组成员之间的相关性的数学方差（t他不同意方差法。
个人影响主题模型（PIT）〔19〕：PIT是作者主题模型。假设每个用户具有代表用户对组最终决策的影响的影响权重，PIT选择具有较大影响分数的用户作为组的代表。然后，选择的用户根据她的偏好选择主题，然后主题生成该组的推荐项目。
共识模型（COM）[38]：COM依赖于两个假设：（1）个人影响是话题相关的，和（2）群体的话题偏好和个人的偏好都影响最终的群体决策。第一个假设允许COM从群体话题和主题用户分布中导出与主题相关的个人影响。第二种假设允许COM聚合组的话题偏好和个人对用户个人变量的权重的主观偏好。
平均矩阵分解（MF-AVG）：MF-AVG是一个矩阵分解模型。MF-AVG将所有成员的项目的平均得分作为项目的组推荐分数。因此，MF AVG认为所有的个人影响权重相等，假设所有成员对团体的贡献相等。