dfs序学习总结

dfs序：

每个节点在dfs中的进出栈的时间序列。

树是非线性结构，根节点连着子节点，那么dfs序...节点进出栈的时间先后？

从根节点入栈，然后左儿子入栈，左儿子出栈，右儿子入栈，右儿子出栈，根节点出栈。

某节点的儿子在序列中的位置大于该节点入栈的位置小于该节点出栈的位置

这样就将一棵树变成了一个区间问题

（从某个节点入栈到某个节点出栈之间的节点都是该节点的子树？？）

例：

1 2 3 3 2 1

1的左儿子为2，2的左儿子为3

1 2 2 3 3 1

1的左儿子为2，右儿子为3

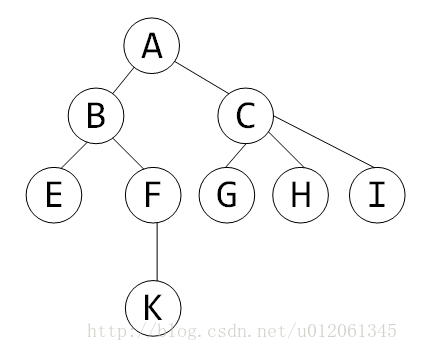
（图片来源于网络）

比如这棵树，我们用dfs来搞一遍

那么这个树的dfs序就是

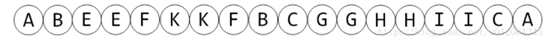
其中每个节点都出现了两次，一次是进入dfs的时刻，第二次是离开dfs的时刻，分别称之为In与Out。在区间操作中，如果某个节点出现了2次，则该节点将被“抵消”。所以通常会将Out时刻对应的点设置为负数。

性质：

现在来介绍dfs序列一些有用的性质：

任意子树都是连续的。例如假设有个子树BEFK，在序列中对应的部分是：BEEFKKFB；子树CGHI，在序列中对应的部分是：CGGHHIIC。

任意点对(a,b)之间的路径，可分为两种情况，首先是令lca是a、b的最近公共祖先：

1.若lca是a、b之一，则a、b之间的in时刻的区间或者out时刻区间就是其路径。例如AK之间的路径就对应区间ABEEFK或者KFBCGGHHIICA。

2.若lca另有其人，则a、b之间的路径为In[a]、Out[b]之间的区间或者In[b]、Out[a]之间的区间。另外，还需额外加上lca！！！考虑EK路径，对应为EFK再加上B。考虑EH之间的路径，对应为EFKKFBCGGH再加上A。

利用这些性质，可以利用DFS序列完成子树操作和路径操作。据传说还有更强大的使用方法，然而我还不会就是

#include<bits/stdc++.h>

#define maxn 100076

using namespace std;

struct treedfs{

int y, next;

}e[maxn];

int lin[maxn];

int tree_dfs[maxn], top = 0;

int in[maxn], out[maxn];

int n, len = 0;

bool flag[maxn];

inline void add (int x, int y){

e[++len].y = y;

e[len].next = lin[x];

lin[x] = len;

}

void dfs (int c) {

tree_dfs[++top] = c;

in[c] = top;

flag[c] = 1;

for (int i = lin[c]; i ;i = e[i].next) {

int to = e[i].y;

if(!flag[to])

dfs(to);

}

tree_dfs[++top] = c;

out[c] = top;

}

int main() {

memset(flag, 0, sizeof(flag));

scanf("%d", &n);

for (int i = 1;i <= n-1; i++) {

int x, y;

scanf("%d%d", &x, &y);

add(x, y);

add(y, x);

}

dfs(1);

for(int i = 1; i <= top; i++)

cout << tree_dfs[i] << ' ';

cout << endl;

for(int i = 1; i <= n; i++)

cout << in[i] << ' ' << out[i] << endl;

return 0;

}

Emmmm这大概就是dfs序的基础代码，输出一棵树的dfs序。

哦天哪，看看这丑陋的代码（捂脸）……

事实上我们也完全可以只记录dfs过程中被搜索到的顺序的先后。

void dfs(int c){

id[++top] = c;

in[c] = top;

f[c] = 1;

for(int i = lin[c]; i ; i = e[i].next){

int to = e[i].y;

if(!f[to])

dfs(to);

}

out[c] = top;

}

在这里id数组记录的就是这个树实际进行dfs的搜索顺序的先后

注：这里in和out记录的位置是不同的

这里in记录的确实按照只记录每个节点的被搜索的先后的方式记录的，out记录的则是以in中记录的那个节点的所有子树的终止位置，这么说可能不太清楚，举个例子

一棵树的关系是这样的：每行为x和y，表示x是y的父亲

1  4

5  4

1  3

2  4

对于这么一棵树，按照以上代码得到的dfs序为：

1  3  4  2  5

而在in和out中记录的分别是：

1         5

2         2

3         5

4         4

5         5

也就是说：

1是根节点，所以1的子树有子树就有3和4 2 5，out中1的结束下标就是5

3没有子树，他在out中的记录的位置和在in中是一样的

以此类推。

那么这个操作有什么用呢？emmmm我也不知道有什么用。

反正他应该和我们最初讨论的是一样的，都是把树变成区间然后用线段树进行操作

拿道具体题看看

Jzoj的艰难的回寝之路，原题是usaco的慢下来。

思路非常明显，dfs序+线段树就可以简单a掉了

代码：

#include<bits/stdc++.h>

#define maxn 500086

using namespace std;

struct node{

int y, next;

}e[maxn];

int tree[maxn];

int lin[maxn];

int n, len = 0, top = 0;

int in[maxn], out[maxn], id[maxn];

bool f[maxn];

inline int read(){

int x = 0;

char ch = getchar();

while(ch < '0' || ch > '9')

ch = getchar();

while(ch >= '0' && ch <= '9'){

x = x * 10 + ch - '0';

ch = getchar();

}

return x;

}

inline void add(int x, int y){

e[++len].y = y;

e[len].next = lin[x];

lin[x] = len;

}

void dfs(int c){

id[++top] = c;

in[c] = top;

f[c] = 1;

for(int i = lin[c]; i ; i = e[i].next){

int to = e[i].y;

if(!f[to])

dfs(to);

}

out[c] = top;

}

inline void pushdown(int pos){

if(!tree[pos]) return;

int lc = pos << 1, rc = pos << 1 | 1, v = tree[pos];

tree[lc] += v;

tree[rc] += v;

tree[pos] = 0;

}

void update(int pos,int L,int R,int l,int r){

if(l > R || r < L) return;

if(l >= L && r <= R){

tree[pos]++;

return ;

}

pushdown(pos);

int m= l + r >> 1;

update(pos << 1, L, R, l, m);

update(pos << 1 | 1, L, R, m+1, r);

}

int query(int pos,int aim,int l,int r){

if(l == r)return tree[pos];

pushdown(pos);

int m = l + r >> 1;

if(aim <= m) return query(pos << 1, aim, l, m);

else return query(pos << 1 | 1, aim, m+1, r);

}

int main(){

memset(f, 0, sizeof(f));

cin>>n;

for(int i=1;i<=n-1;i++){

int x, y;

x = read(); y = read();

add(x, y);

add(y, x);

}

dfs(1);

for(int i = 1; i <= n; i++){

int k;

k = read();

cout<<query(1, in[k], 1, n)<<endl;

update(1, in[k] + 1, out[k], 1, n);

}

return 0;

}