HDU 1180 诡异的楼梯（超级经典的bfs之一，需多回顾)

传送门：

http://acm.hdu.edu.cn/showproblem.php?pid=1180

诡异的楼梯

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 18382    Accepted Submission(s): 4864

Problem Description

Hogwarts正式开学以后,Harry发现在Hogwarts里,某些楼梯并不是静止不动的，相反,他们每隔一分钟就变动一次方向.
比如下面的例子里,一开始楼梯在竖直方向,一分钟以后它移动到了水平方向,再过一分钟它又回到了竖直方向.Harry发现对他来说很难找到能使得他最快到达目的地的路线,这时Ron(Harry最好的朋友)告诉Harry正好有一个魔法道具可以帮助他寻找这样的路线,而那个魔法道具上的咒语,正是由你纂写的.

 

Input

测试数据有多组，每组的表述如下：
第一行有两个数,M和N,接下来是一个M行N列的地图,'*'表示障碍物,'.'表示走廊,'|'或者'-'表示一个楼梯,并且标明了它在一开始时所处的位置:'|'表示的楼梯在最开始是竖直方向,'-'表示的楼梯在一开始是水平方向.地图中还有一个'S'是起点,'T'是目标,0<=M,N<=20,地图中不会出现两个相连的梯子.Harry每秒只能停留在'.'或'S'和'T'所标记的格子内.

 

Output

只有一行,包含一个数T,表示到达目标的最短时间.
注意:Harry只能每次走到相邻的格子而不能斜走,每移动一次恰好为一分钟,并且Harry登上楼梯并经过楼梯到达对面的整个过程只需要一分钟,Harry从来不在楼梯上停留.并且每次楼梯都恰好在Harry移动完毕以后才改变方向.

 

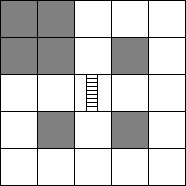
Sample Input

5 5
**..T
**.*.
..|..
.*.*.
S....

 

Sample Output

7

Hint

Hint

地图如下：

 

Source

Gardon-DYGG Contest 1

 

Recommend

JGShining   |   We have carefully selected several similar problems for you:  1175 1072 1240 1253 1242 

 

分析：

超级经典的搜索问题之一

需要注意的地方：

1.要搜的点有没有越界

2.要搜的点是否搜过

3.要搜的点是不是障碍物

4.如果要搜的点是楼梯，判断楼梯此时的状态，是能直接通过楼梯，还是需要等楼梯翻转过来

5.楼梯对面的点如果搜过了，或者越界了，或者是障碍物，那么就没有走楼梯的必要

本题的重点在于楼梯状态的判断，因为楼梯状态是随时间变化的

code：

#include<bits/stdc++.h>
using namespace std;
#define max_v 25
struct node
{
    int x,y,t;
};
char G[max_v][max_v];
int vis[max_v][max_v];
int dir[][]= {{,},{,},{,-},{-,}};
int n,m,sx,sy,fx,fy,tme;
bool isout(int x,int y)//判断能否继续搜
{
    if(x<||x>=n||y<||y>=m)//越界
        return ;
    if(vis[x][y]==)//搜过
        return ;
    if(G[x][y]=='*')//障碍物
        return ;
    return ;
}
bool isgo(node t,char x,int d)//判断是不是需要等待楼梯转动
{
    t.t+=;
    if(x=='|')
    {
        if(d%==&&t.t%==)
            return ;
        if(d%==&&t.t%==)
            return ;
        return ;
    }
    else if(x=='-')
    {
        if(d%==&&t.t%==)
            return ;
        if(d%==&&t.t%==)
            return ;
        return ;
    }
}
void bfs()
{
    memset(vis,,sizeof(vis));//是否走过标记位重置
    queue<node> q;
    node p,next;
    p.x=sx;//起点初始化
    p.y=sy;
    p.t=;
    vis[p.x][p.y]=;
    q.push(p);//队列初始化

    while(!q.empty())
    {
        p=q.front();
        q.pop();

        if(p.x==fx&&p.y==fy)//判断是否到达终点
        {
            tme=p.t;
            return ;
        }

        //四个方向搜
        for(int i=; i<; i++)
        {
            next.x=p.x+dir[i][];
            next.y=p.y+dir[i][];

            //判断越界
            if(isout(next.x,next.y))
                continue;
            if(G[next.x][next.y]=='.')//可行点之一 .
            {
                next.t=p.t+;
                vis[next.x][next.y]=;
                q.push(next);
            }
            else  //如果是楼梯
            {
                if(isout(next.x+dir[i][],next.y+dir[i][]))//判断楼梯对面点能不能走
                    continue;
                if(isgo(p,G[next.x][next.y],i))//楼梯不需要等，直接走
                {
                    next.x+=dir[i][];
                    next.y+=dir[i][];
                    next.t=p.t+;
                    vis[next.x][next.y]=;

                    q.push(next);
                }
                else //需要等楼梯翻转过来才能走
                {
                    next.x=p.x;
                    next.y=p.y;
                    next.t=p.t+;

                    q.push(next);
                }
            }
        }
    }
}
int main()
{
    while(cin>>n>>m)
    {
        for(int i=; i<n; i++)
        {
            for(int j=; j<m; j++)
            {
                cin>>G[i][j];
                if(G[i][j]=='S')//找起点
                {
                    G[i][j]='.';
                    sx=i;
                    sy=j;
                }
                if(G[i][j]=='T')//找终点
                {
                    G[i][j]='.';
                    fx=i;
                    fy=j;
                }
            }
        }
        bfs();
        cout<<tme<<endl;
    }
    return ;
}