《Deep Learning》第二章线性代数笔记

第二章线性代数

2.1 名词

标量（scalar）、向量（vector）、矩阵（matrix）、张量（tensor）

2.2 矩阵和向量相乘

1. 正常矩阵乘法； 2. 向量点积； 3. Hadamard乘积（元素对应乘积）

矩阵乘法服从分配律、结合律，两个向量的点积满足交换律，利用两个向量点积的结果是标量（scalar），标量转置是自身。

2.3 单位矩阵和逆矩阵

逆矩阵一般作为理论工具使用，计算机由于精度不足，一般不使用逆矩阵。

2.4 线性相关和生成子空间

线性方程组，解的个数：0、1、∞，不存在有限多个解的情况。

线性方程组，只有方阵，且是非奇异的（所有列向量线性无关）才能用逆矩阵求解。

2.5 范数(norm)

将向量映射到非负值的函数（衡量向量到原点的距离），满足距离三要素。

范数分为x范数和L^x范数，例如L²被称为欧几里得范数。

L⁰范数（在数学意义上是不对的）：非零元素数目个数。

L¹范数：常用于数据集中于原点附近；零和非零元素差异非常重要；非零元素数目的替代函数（因为L⁰范数对向量缩放无感知）

L²范数：欧几里得范数，其平方值常用于衡量向量的大小，可以简单的通过点积运算。（在原点附近增长的十分缓慢，此时推荐用L¹范数）

L^∞范数：最大范数，最大的元素的绝对值，即||x||_∞=max_i(|x_i|)

Frobenius范数：常用于衡量矩阵的大小，在深度学习中的最常见做法，计算矩阵每个元素的平方和后开方，类似于向量的L²范数。

2.6 特殊类型的矩阵和向量

单位向量（unit vector）是具有单位范数（unit norm）的向量：||x||₂=1（欧几里得距离为1）。

如果两个向量不仅相互正交（点积为0）且范数为1，称为标准正交（orthonormal）。

正交矩阵（orthogonal matrix）：行向量和列向量分别是标准正交的方阵。

2.7 特征分解

将矩阵分解为特征值 λ 和特征向量的表示形式。（一般只有方阵才有）

可以看作在二维平面上画出特征向量后，乘上矩阵A表示这个向量被拉伸了 λ 倍，如下图：

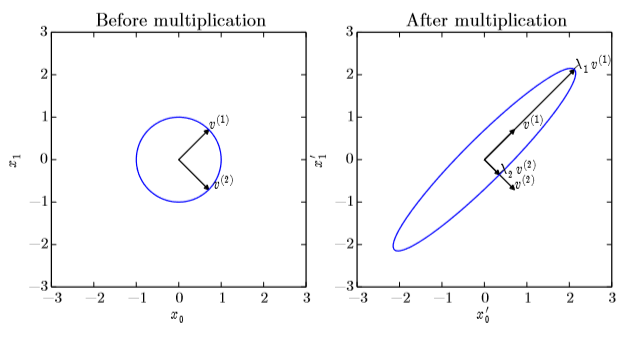
λ > 0：正定矩阵（positive definite）

λ ≥ 0：半正定矩阵（positive semidefinite）

λ < 0：负定矩阵（negative definite）

2.8 奇异值分解 SVD

这里书里讲的不是很清楚，推荐一个视频：https://www.bilibili.com/video/av15971352

博主先在这里说说自己对SVD的理解：就是

提取矩阵的特征，按特征的重要程度从大到小排序，每个特征的权重就是奇异值，特征本身就是奇异向量，当保留权重较大的几个特征时，能够很好地还原出原矩阵。

因为非方阵的矩阵无法计算逆矩阵，所以无法进行特征分解，故提出了奇异值分解（singular value decomposition）。

每个实数矩阵都有一个奇异值分解，但不一定都有特征值分解。（例如，非方阵的矩阵没有特征分解，这时只能用奇异值分解）。

且奇异值分解有着更广泛的应用（例如特征降维，矩阵去噪）。

博主对原理的理解：SVD就是分别计算A^TA和AA^T，让其变成方阵，然后对角化，从对角化后的信息中提取特征，经过转换后作为奇异值，从而复原矩阵A。

2.9 Moore-Penrose伪逆（广义逆矩阵）

A⁺=VD⁺U^T

U，D和V是矩阵A奇异值分解（SVD）后得到的矩阵，对角矩阵D的伪逆D⁺是其非零元素取倒数之后再转置得到的。

当矩阵A的列数多于行数（矮胖）时，用伪逆求解线性方程是众多可能解法中的一种。但是x=A⁺y是方程所有可行解中欧几里得范数L²最小的一个。

当行数多于列数时，可能没有解（因为没有满秩），在这种情况下，通过伪逆得到的x使得Ax和y的欧几里得距离||Ax-y||₂最小。

（这部分没怎么查资料，暂时不知道其在机器学习中的应用）

2.10 迹运算

没什么好说的，对角线元素的和，以下是迹运算的性质：

一个矩阵的转置不影响迹的大小；

多个矩阵相乘，将最后一个挪到最前面之后，迹是相同的（ Tr(ABC)=Tr(CAB)=Tr(BCA) ）。

标量在迹运算后仍然是它自己。a=Tr(a)；

循环置换后矩阵形状变了，也不影响迹的大小。

2.11 行列式

det(A)等于矩阵特征值的乘积，用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。

2.12 实例：主成分分析 PCA

关键词：单位范数、L²范数、最优化问题、向量微积分、Frobenius范数……

这块有点困难，之后补上。