day-11 python自带库实现2层简单神经网络算法
深度神经网络算法,是基于神经网络算法的一种拓展,其层数更深,达到多层,本文以简单神经网络为例,利用梯度下降算法进行反向更新来训练神经网络权重和偏向参数,文章最后,基于Python
库实现了一个简单神经网络算法程序,并对异或运算和0-9字符集进行预测。
一、问题引入
利用如下图像结构,通过训练集对其参数进行训练,当有新的测试数据时,通过更新函数,获得正确的预测值,更新函数方程为:
Oij
= activation(sum(xi*wij)+bij)
图中为简单的两层神经网络结构,4,5对应的为隐藏层,6为输出层,
activation代表激活函数,常用的有logistic和tanh函数,b称为偏向。
二、神经网络正向更新和反向更新规则介绍
对于正向更新:
Oij
= activation(sum(xi*wij)+bij)
对于反向更新:
对于输出层:Errj
= activation_derivate(Oj)*(Tj-Oj)
对于隐藏层:Errj
= activation_derivate(Oj)*sum(Errk*Wjk)
delta(Wij)
= l*Errj*Oij
delta(bj)
= l*Errj
wij
= wij
+ delta(wij)
bj
= bj
+ delta(bj)
其中:
j代表第j层
k代表输出层
T代表实际标记值
O代表输出值
activation代表激活函数,常用的有logistic和tanh函数
activation_derivate代表激活函数的倒数
三、一个简单神经网络的数学运算实例
我们以一个3×2×1神经网络为例,说明如何利用正向更新和反向更新来训练神经网络,完成一次更新:
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfgAAADrCAIAAAAKfxOpAABb40lEQVR4nO2dCVzM2/vHZ9+bmaaZ9n0TqRClLJHtFoWkULayFVmubCHLlX2XXRIu2SkkS5aELJEQqaR935tqmuV/1P27/aw1+3TP+zUvZr7z/Z5zpvnO5zznOc95DkYgECAgEAgE0nHByLoBEAgEApEsUOghEAikgwOFHgKBQDo4UOghEAikgwOFHgKBQDo4UOghEAikgwOFHgKBQDo4UOghEAikgwOFHgKBQDo4UOghEAikgwOFHgKBQDo4HVnouTx+en5NVlFNQVldeU1DdV2jQCAg4rFMOlGTQdJRpXTSpuOxaFk3EwKBQCRLRxN6vkDwKrM89ln264yS3MJKHp+Pw2JxOAwWi8ZiMCgUksfjczjcJi6X08TjcJqYymQrI9VhNrp9zDXQKKSsmw+BQCDip+MIfVlNY3jsh5tPM2tqG2hUkjKN0rWLHomI/8UlfL6guoadmlv16O2TxkZOb3OteW7d9NSVpNZmCAQCkQIdQehLaxr3XEq5n5SFQqF0tJhdOyshkW2yzYGBT6eRwcMAgQBm/ufC8gnrrlsYshZ6dDfRVpZ0syEQCEQ6KLbQA5P8RFz60ehkHA5jqK+uTKcIXRQoQV9XFfQT+YXlUzbcHNBdZ8VEGyJesf8+EAgEglBooa+obVoW9uR1Wr6JoQZThSqWMtHoL2MCTXXG60+FY1Ze3RngYKoDTXsIBKLYKKrQp+ZUBe570MBp6m5pSMBjxVs4kHtTY83ikqppW27NG9N9jIOJeMuHQCAQaSKM0HPzTnt0nZDkFfdy90BlVPMhQc3jJdb2+42OvomaqgdkV8BOv7Biks+OxwY7M1/MMxBzd5KSVTF/z10KhWhlqt1Gd7wQqLJoSkrEfVdeV9Y2+g7vKqFaIBAIRNIII8EYLc8jZ+93G+oZMORNxEhVNIJfEbfEc0uV1+Vjk76oPDfntI/jzIROLmaEx41ib3FmUS2w5SlkorGBhtgL/wYiAdfZTPfEzVQNFbJzbwNJVweBQCCSQDhbG8UYvPVi8CO7ST5D31z2xsfMnXAQO+/uXle15tVH3Np6i5Cn+51LA/RPvxBraxEVtZz5offRGLSRgbp4S/4ZeBy2S2e9zaefU4jY/lba0qkUAoFAxIiwThUkpefyCzvud5vlsTyLcfis1pqn6/vT/nGiEDr7LOqMQNQ9FFsrWxAgEMHHntaxOVZd9SXnsfkeYNebGmuvCn98OthZnUGWWr0QCAQiFkTwnuNM/P4+fNPMa1Wt9fa0xVYk8TXqJ9x6mf8iNbe7haE0Vb4FJSWipjpj25kXW/z6S7lqCAQCERFRpkn55cl3kthEJeS7izFZ/iamv1qEKjIcLn/vpVcaagwCASfJen6Kqirj1dvM5x+KenZSk0kDIBAIRDiEF3pu9ompE07rbX0awVxm7TN2Y7/Hq7pL0Kr/Oy69vKK2Z3djyVXxa1AopK6O2ubTz86sGiH1EQUEAoEIj7BCX/92h8esB3Z7U+Z01UMdPnrVfKz7csek7f1oEpFAgQBxOf6jthYThUJJovw2QqdTykorHr3J72OhKcNmQCAQSLsQSugFVQ9XjF6a7nr2zeQv4ZQI9dF7T06xcPaYP+R1mDML2VRVWFjNRbCLarmCxor8nBwMBk1W1WDghe4EUrIqiktrbPSlFGnzC1QY1DtJ2VDoIRCIAiGE0POKouaM2c6ednP/aPV/krmjmH9sPz0nbuCEGUPfnhtVsKpXr115/5y9pq/hGgSCPOZWwfnBQqeFjHr8iUolYdCyzx1PpJDuvcwK8rbBoGU5toBAIJC2I4TQo9VGnigSfHMQSR+wJ0uwp/m51s5cwU6RW9aa56kFLKZ4stmICB6HZdJJT1ML7btCox4CgSgGCpDrhsPlF5XW6OqK4rcRcIvvJBxe/SJdc8Dm0z1YIo0MVFWorzNKoNBDIBBFQQGEPqe0ji8QYIXf849Xk7jq3LFkRjd9TDpH9PZgsJi8klrRy4FAIBDpoABC/7moBi9SXnheE8ekb/Byg9pNhxPfid4ePhJVXAmFHgKBKAwKIPSFZWw8TpRExDhGv8kMBKLpo3jag0KjSirrxVMWBAKBSB4FEPraBg4GI/t4m6+g0ZjiCrasWwGBQCBtRQGEHo9BCwTfRvnIEAwaSSaKeasTCAQCkRwKIPQaKuRGDlfWrfgXAY9HElQBaDSarNsCgUAgv0cBhN5Ek8ZpbJJ1K/4FhxI8Pr9Zfd9sZ2fnCRMmgH+JRKKsGwWBQCA/RQGEXk+dwuXxBAKBkNmJBdzGqlIOH8GtYgsETY2VhTVoNBLPoJCFzIKJRgqmL911aqs/mUw+dOjQ9OnTR4wYMX78+MGDB2Ox0KUDgUDkDgUQehQSSaMQausalChCGc5NaY/XeiVV/PPq8foRjxEIbM8DM2fbCqf0FZV1DlaGk2NjgbJv2rTp+PHjZ8+eXbdu3eTJk93d3YHi9+nTR7bJ1yAQCKQ1CiD0AJsumm+zq4QUelyXAdtfDhBTS9AoRHJW6XJvGzUGKTo6etCgQadPnw5oJisr68yZM+BJWVmZp6cnUHxra2sxVQuBQCDCoxhC7zHAePbOu4b6st/xg4pF6KoqAZUHzy0sLK5cueLq6nr16lVbW1t9ff0lzbx79w6o/7hx44BdP76ZTp06ybrhEAjkv4tiCL2lIZOIQ9fU1gtp1IuPqqqawT31vr60s7MLDw8fM2ZMbGysubl5y8EuXbr81cyzZ88iIyOB1c9isSZMmADMfF1dXRk1HAKB/HdRDKEHuPY1vp74uXMnHRm2gaWEvfmqcMn4nq0PjhgxYtOmTU5OTo8ePdLW1m79Vq9mtmzZ8uDBA2Dj9+jRo3PnzsDAHzt2LJB+6bYdAoH8d1EYofdx6nLh3oeqajaNKvltyH9CcVHZmP4mTNq3owovL6/y8nJHR8eEhITvFRyFQg1oJjQ09ObNm8DGX758ua2tLVD8UaNGwWB8CAQiaRRG6El4zFz3HnsuJnezMBAyzlI0NGmYuNSydb72P3w3ICCgqKjIxcUlNjb2Z9qNxWKHN1NfXx8VFQUUf968eYMGDYLB+BAIRKIojNADRvc1unDvY15BmbYmU8pVKxExT5M/B4zpTvp5Hs1169YBu97NzS0mJgaH+1XoJtB0z2YqKysvXboEg/EhEIhEUSShB2ya2XfCX9cpZCKdRpZapTgMqqas3FCDOqyX/q/P3LNnj7e397hx486dO4duw8aHdDp9ajNgNACD8SEQiIRQMKHXYlF2BgxYEHrf1ERbOhE4aBQS18QuqW0Ine/4W48REPeIiAhnZ2d/f/8DBw603cWkpqbWzmB8btnHHIyhAU2O0npCIBA5RcGEHtDdRHXN1N7B4U+6mOmSiHiJ1oVBo2goTsqnssOLhxJwbfpb4XC4qKgoR0fHoKCgDRs2tLfGtgbj84ujfEek7Hix3ZrQ3iogEMh/DcUTeoBDN51lXrwNJ58a6GuoMJQkVAsZj+bUVL0uqNo9dyClPXmJSaQvi2aB1jOZzIULFwpX+2+C8Xl1ZWw0CfdlxCCoerhszFaN0DPzzH7U7Qm4DVw0ASuD6WsIBCInKKTQA/6w0ddVVQrc94Bdx9bSUkWhxCxkmjTs45eZXQ2YR5cO+8UE7M8AohwTE2Nvb6+qqjpx4kRRWvLjYHz3ftm1AnUg34Lqh8GTNt1BLW/ZDZdf8fzsLcHQMb0YaISgMffegZWBK49Xz335Zp2lZAc/UoXPF2QV195/nZ+eW1laVV/Dbqyrb+I0cQWgeybgKCSsCpWowSBbGqkMsNTC46B7C/JfR1GFHtBFX+XsmhFrjz1Oef9ZW5tFpYpnepZKwKC59TcTMuaO6T7czlDocrS1te/cudO/f38ajebq6ipiq74Nxj+55+zHVMOZIxh9EdvOqdrpIrXo4Kvk5Z+fOWaD6QUXD9ABPA6Zva+mp5U+RVd7pEmHUPkGDu/a0+y4l7kfs8uqm5dJk0l4HA6Lw+IZJFLzNmTIpiZuE5ebW9aQUVBz42nWqrAELVWqTWeNUX0MOukoy/oTQCCyQYGFHkAhYjf79b+blBN66VVRUZmqKoNGowhdGo2IbmKzHz5Lt+2sEb50mCZT+KJaMDExuXLlSsuqKAcHBxFLa+GfYPz+2Ko7ZWqudltXbc7mI6v5Sln3LldZ50+enzn9RkTPL10e1W7FCbv6Z/O7ktyCLBQ9RL+4quFITOqdp5+auDwVBlVbi0mjktoSlcTj8Sur6h6lFl1NSFdjkGe5Wg62luXiaghEJii20LcwsIeOQ3ft+y9zw66/Kcgv1dViCDA4Mqmts5R4DJKMFlRW1TxILhrQXfvokmE6qmLz+9vY2Jw8eXLs2LHAurewsBBXsYim6qomgWnK6bqhx16uyndxPH83fPse38cUK5eAvHtNnf8Jxme/johCj7lg/qM/BbfwetDkbTU+x/Z46sjxXVBVx9lxMeXui08YNEpHm9XeKRk0GgUuAQ+BvnpJWXXIyae7L7ycO6bbYGuYdAjyH0KOf+LtAYVEArkHj1fpJXFJ2U/eFnyoZOtrKtOpJCQGw+UjwQ+ej0DisGgEn49ECHBoBAaJ4HA4OQWVOcU1FobM3uYai8f1ZNHFb/s6OjoePHhw6NCh8fHxxsbGYinzy1xs7Yvt0a4nX7sbl64gqFn7Wt5extngN5a0ad26af8E449GnryKc7/S5Xudr08LnzrU78xn0vhFNDm+Be68yt986imXJzA20BBx5QQSiVRl0sCjrLxm/cln5+9/3DyrH5Uk5OYzEIhiIce/cqHoZswCD/CkpLI+MbXgQ3ZFYXldTU1DRW1jWVU9u5HLUCIoK+FVqERlKkFflTK6j4GVEetLByBJRo8eXVJS4uzsfPfuXS0tLdELBEJfyyX/sSPUQwvdkPa5NO9R0KnO254vnKqHWTP//4PxZ/unv8uz8D725oV362B8fmXi5glzUpzWTH8RVDXNlip6ayQAl8ffdC75enyapgZDV1ucCeCAda9Mp3zKLnJbEb3Vv3/L3QKBdGw6mtB/BdjmI+wMR9jJuh3/z4wZM8rLy52cnIBdL3oiM1ynBbffjCGZ6WAQgsbSvJLqipGnjkzS++fbbAnGn937vbHvH900Ka2D8Y2oHxeOXFax4OoB88O9Ng09aCOp4FRRqGvkBoTGf8wq6WKmQ1USfw47FApppK9eXlEzb/fdOW7dxg4wFXsVEIhc0WGFXg5ZunRpWVkZ0Prbt2+TSKLpF5KoZf7P+imi1ZzNO5lTgG3f8ppfl5fNZuoRnh65xZp6a9fyzrj1/wTjOzrYsSvZRu4Lz/bhZO4/y/4jzFrU+WbxA1R+zp74rLzy7pZGWEmOtBjKSiQSYf+V13y+wNMR7gwD6chAoZcqmzdvnjx5MjCxz58//+vEZ20GSTIdu6i1SVr77K/BQyMaDBmlAqcrzBal7NWrV3f11A8nKZylB/UKbtt070VgNxjMflFfYkaRp8z4PL5g6ZHEjOzSbhYGElX5Fgh4rFkn3X2Xk9VVyA5W2r+/AAJRTKDQSxUkEhkeHu7m5ubj43PixAmJ5FumDjjwsTLo0eWTxyOOj9VQ77M3MWqmIRbRVFVF02k8u3GhrfuklUF/hGyupeS9MDVdI1eZ8TedS371Ps/SXB+LldKdSSTgOpvprjr6ePfcAZZGctTnQSBiBAq9tEGj0adPnx4+fPi8efN2794tkTqQJN0+E4LAY2/lp098neb0DcSuAX8/n3M4G/QA4XtWnylhG/Ko0w/c2yF4f+eMfGTGf/Kh9OqDD1076xIIUg2GIZMIBvrqQYceXlznKulpeQhEJkChlwEkEuny5cv9+vULCQlZvny5BGvC0A1MWr9u7gHmIR8cjLM8vLPXu7t5POKfnp7j5CAzPofL3xL5XI1Fk8m2wAxlparKmvCYtzNdLaVfOwQiaaDQywYajXbnzh17e3sGg+Hn5yfNqpsKXuUZTQ4Z5WI5zuXrQZlnxo+8n1FYUtWru8nvT5UMmpqs03feu9gbir4iGgKRN6DQy4yWxGfAcAZa7+npKbV6scb+0XE/fbf9mfHFQBOPf/LGWwNdNTRaZnut4PFYfW3WvsvJ66b1kVUbIBAJAYVelhgbG0dHRw8aNIjJZIJ/Zd2c/6GtmfHFwe2X+XX1jaosGc8G0xm0+OT0GjZHCa6YhXQsoNDLGAsLiytXrri6ul69etXW1lbWzfkBv8mMLw6iEjJZKjSZ7PneGjCe0FKl3X+VO8Je+KylEIgcAoVe9tjZ2YWHh48ZMyY2Ntbc3FzWzfkpP86MP3782LFjWSIE4zfx+O+zSowMNMTYVKGhUMm3X3yGQg/pYEChlwtGjBixadMmJyenR48eaWvL9cqdbzPjR0YuX77818H4AoHg7NmzP5uHePqhhMPh0qgipjrg1ycHH9t5jTj28iRnPaE9/SQy6dXrdHZDE4kgvYgjCETSQKGXF7y8vMrLyx0dHRMSEkQxkKXGP5nxhw+vr6+PioqK/HkwPui9xo0bd+PGjX379n0fpP8yvURJSdSQSkFtwv3wmEYEQsSC0GgUi07KyK+yMGSK2CQIRH6AQi9HBAQEFBUVubi4xMbGysM61TYCtNuzmZ8F44M+AJx27NixV69eAdPexOR/Yihzi2sJeNEmPwWVWZFrP+lNtyg8kiNSQV8gE/EllWyRi4FA5Ago9PLFunXrgF3v5uYWExMjpmQ40uOHwfjgs4DnLScAoe/VqxdQ/FGjRn29qqKmAYcT5T7k16dsu5lsPjB4cNX2IyJ9gGZIRFxRORR6SIcCCr3csWfPHm9v73Hjxp07dw6NVsgV+a2D8YHcV1RUfH2rqqoKSH9gYOD69esxmC+3X3VdIx7f1u3AvkdQ++h+eLzahDOmyvXPxNB2BImALamqF0dJEIi8AIVe7gDiHhER4ezs7O/vf+DAAZkHHYqCvr4+j8f75qBAINiyZUtiYuKZM2fU1dW5XB6eJOzs6RenzZpM3cCJtmoofpaIrW0Bi0XXN3LFUhQEIidAoZdHcDhcVFSUo6NjUFDQhg0bZN0c4WlsbLx06dIP33rw4EH37t2B1hMJ2Cbut51B2+DXp2y/+cpswFonJdBT8EVp6b/wuHylNm84DIEoBFDo5RQSiRQdHQ20nslkLly4UNbNERI+n3/nzh3wb1VV1deDbDY7PT29uJnNmzer2fnWc4VLL8MuuHmtro5/c3Hvm+CVANTDR5xzC73vMfavJRrCTnDUN3BSEuKyeyiLazkYBCJzoNDLLy3JcOzt7VVVVSdOnCjr5ggDBoPJz8/Pysr6/Plz1v9TVlbW8i7ozIyMjPpP1Hv4tkio4sm6s2Kmc/7fkudmv9zql97r4JghphQRguAbG5uqi3N69OgxYMCAgIAABwcH4cuCQOQDKPRyjba2NrCI+/fvT6PRXF1dZd2cdoPFYkNCQhITE79/C41GA9N+3rx5dE3a7RfCRUUiMRTVfze95Tbg0UgUmaVEp4qSGq2ytuGvvzYc2bv1xIkT/v7+oK8Ccu/l5SWrNP0QiOhAoZd3TExMrly50rLoVBGty+XLl/+wi+LxeFQq1dPTk81Fbzv9jM8XoFCiTTtj9G03PBcxW5ASAV1aVW+gQcVh0X5+frNmzbp9+3ZoaGhQUJCPjw/QfejPgSgiUOgVABsbm5MnT44dOxZY9xYWFrJuTvsYMWKEpaXl69evv3/L29ubAkAgVBmUyqpahrLS9+dIGT6nwb6r5td9ppBI5JBmMjIy9u3b16NHD9DXzp07VxF7XMh/GSj0ioGjo+PBgweHDh0aHx9vbGws6+a0FT6fHxUVVVdX98N3Z86c2fLE0Vrn5otceRD6/MJKr8Fm3x83MjLatm3b2rVrjx8/Dv05EIUDCr3CMHr06JKSEmdn57t372ppacm6Ob+By+WeOXNmw4YNJBLJ19d3+fLlAoGg9Qn29vbA0m95Pm6gyelbqaBXkMJWVr9AlYJ9kVTRx0LzZyeQyeRv/DlTp06dPXs29OdA5Bwo9IrEjBkzysvLnZycgF0vt8lwGhsbjx07tnnzZh0dnR07dgwZMgQcrKmp2bp1a1NT09fTwGf5+lyVTrIyVs0rKNfRkmUqscqKytH9jH+7P/hXf05mZubevXuhPwci/0ChVzCWLl1aVlYGtB4YlcBYbj7GL46a5fdxwemFnWWbHKeuru7gwYNA3K2srE6cOAFs9q9vrV69evz48S4uLp8/fwYvlZWVPTw8Wl+7wrvXuLXXVVk0PE42+YFVSKgHz4rOrB7e9ksMDQ2/8efMmTPH29sb+nMg8gYUesUDGMuTJ08eN27c+fPncTicoObxuoV3tY5tk2EC9YqKCmDb7t69e+DAgdHR0d26dfvmBNDOgoKChoaGfv36geHIpEmTvlFDbVWlkX2N76cUdjKRgVcKj0V9zCyYNdKSRsa399qv/pw7d+7s2bNn+fLl0J8DkTeg0CseSCQyPDzczc3Nx8fnxIkjqaFzL1lufG6nJJOcOEVFRcCEP3LkiKur68OHD01NTX94WkpKCjB1QR9gbW0NZPHrNGxrAtys7rzILi2rZqpQJdzqb1HG8oqQSNc+RkKXAL6Uwc209ucEBAQMGDBAfM2EQIQECr1CgkajT58+PXz48ABfl483cAsfuKpJfRYzOzt7y5Ytp06dmjBhQlJS0i8M2JKSEhcXF9AftGyKe/jw4R+eRsBhtvr3999+B4/Dir4VSdvRoKBuJ6YfXjQEJY78cV/9OSdOnAB2PfTnQOQBKPSKColEunwxvJuhaY2570Xj/3fb8GvTbvz9gDpmal+m5BIcp6Wlbdy4MSoqatq0aampqaqqqr84mc1mA5X39fX18vL6bcldDVQ2zOi7/EiCWScdslQyi2nTsTcevt8220FHVZzBnWQyedasWWDg0tqf4+/vr6enJ8ZaIJA2AoVegcFm7McQnHH5t4/v3+83zf35mR1/rdsd9aFOfYaZRx8HqgRcOa9evdqwYcPdu3fnzp378eNHZWXlX58vEAiAwBkbG69YsaKNVfSx0Fw8vufm0887m+mSiO32mLcLPQY26m7qhpl9uxpIJNrnqz/n06dPoaGh1tbWP/fnCMDpkmgDBIKAQq/ANKUfmntCf82j3fafBzq47AkKyNYcPcdtcFIYavuavmJX+UePHq1fvz45OXnBggVHjx4FFmtbrgoKCsrPzwdWbbuy6jv3NkChkBv/fqajzVJl0YVs8S/BoFE0FOfag4x10/v0MlOXRBWtMTAw+N6fA4Y4/x83haiL93eK9I7Z26dNf1YIpJ1AoVdQeAUXFx+gzV1Rt3aiwzlc55E5b2PObuwXO3eFwerkUeridNvcunUrJCQkJydnyZIlFy5cwOPbamUfP378/PnzoIcQYk/EP2z0TbWVF+1/kFVXr6OjhkaLcwpClYrLyioo4/Iigv5QZ0hPWr/6c+Li4nbv3t3Kn6Nb+zm1kPdPrp+G7GepGMtumnho4UPEBRR6hURQFb9mYXQx5uMJwxnrn+4ZbEROfBw/fIgjR93n8VSDf+MsuXWVXCKdIIxKtmQvAFY8m81etmyZp6dny85/bQRoWWBgYEJCAovFEqJ2gKEm7e+VTtvOvLj/KktDg8Fg0ETNeoZAKOHRGF5j3KMM1z5Gs0ZaoUUuUAjA4GZQM638Of2cCJ+VLFXAF8cvu7Wg37DoUYkfd/WCs7cQcQGFXjFBswaHRC1wG9ZJ6R8RtzWpNMcxX1VfRWa8RZibC+qz4o5s+mvrhfrJV++ssaG0R9BaZy8ICgpydXVtb2aC9PR0Ly+vyMhIExOTdl34DQQcZvlE21F9y45cS0lOydDXZlLpVOGseyYFy66pSXiWa9dVc/+fg0EvIkrDxEIrf87hvxZfLXs4Opw+CXV1Z2S1knkP7S/jJkFt8qF1cZZL59nR//3Mgrrs9xVMM20SNPghbQYKvUKCpJi7TzZvdaD+9Y6ln52PbPmj0nnY4GUePQ+cSMQMnb/yRrpr53YkZ/9h9oL2UlJS4uTkFBIS4ujoKMTl32NuoLJjzoCMvMrwmLfxyenaalQKhYzB4wmE33iEgMFOxAj4nMbCkuqklxVDe+kfW/aHFku43awkxRd/zrRRTWHbroxbe3rX9AcfG3ow8dqUShSClXt22sidrLCEf79BAfv9cX+XKRFl3rezTgyS9moDiOIChb4jwMs9s/Rcl43n6eywHXVlDQuPJp68+2J0d52223y/yF7QLjgcjoeHh7u7u4+Pj3Al/AwjLfq6aX2q6zhP3xcmvitIfJff2MRXUyET8FgcFoPHYbAYNAaD4nDAgITX1MRlNzRlF1bRKXibzhpDhnbu2UmNRJDh2uFfwilMLaOY42Ovl/ZaF+V1wnPJ1en9XENZ75Px8xOODWL8o/MNmecWTdn0BsMn6E4KsOsgKi9AIGrYTYUV9aVV9ZW1jRg0kkEl6LIoqnTouBInUOgVH0H1w5D16doGG52n63svi82OubxrzWa/sYNiY9uS+Oy32Qva0RCBAOg7g8FYv3690IX8GioZN9haFzzA84KyOmDmV9Q0lFU3lNc01NRx+DyeJp2gQiUoKxFUaERjLRqLTpJQS8RJQ96H4ry04BsDwp/92eXCRaUBf18euGrwsmIa8+g4W/KX+ByPirshE4IyPSPODVhlVxUwu/vXj9VUELd3zc5Lbxu0+k1cvNirG12W+T/bRllNY9yr/CdvC9Jyyiuq6pq4PCQSicNhMGg0eMJp4oJ+WiBAEAlYDRVKd1NVZxu9rgYqsm61YgOFXvGpfXnmKaO3++wVV0aYNbvse65bV15e7ubmFhMTI8iNWrs28lV2XmElumtAxOGpRl/9HW3MXtB2Nm3alJ6eHhcX165gSqHRUCGDhxQqkjScovd5dTXEWTF7XdW48YmFSugzk5ZiAm/nLu+eeDdu964ti+fPFtC67bh8eiLtet9Eq0UHjf4Zm3A+HfPoPTfLecXCANVPkSv62L+992xjLzn9m9RzeJH3Mm4kZuYUVoHhlzKdrKJC09NVw2Ix30+z8/l8MDirqWt4+KYwOiED3NY9OqlNG25urg8VXxig0Cs+Sg77Xjz55tiePXu8vb3HjRt37ty5kPA/Xod6DP2LO8FKtUUg2p69oO2A0vbt2/fs2bOvseGQNoLRclm7t1M3nz5UJC/73dvcDy9uu518sawHBYUY1FcnbfeH1wOCHYwrFznbnFThZHZfO1y9xWrnpIVOWJg183b8GpsviY5GmBV1GXf87apeNvLm9aip5x68/i72SWZjY5OmBqOHleFvc5SiUCgCAQcerObER/UNnLyy6lnb7uiqUeeP7d6rk5pUGt5xgELfMUGj0REREc7Ozv5+vt6aaSPDtLc+PO5jSmhX9oK2k5iYGBgYGBsbq6YGf4HtBkW19PBv2YOlqTyHTTILvHh0gk7zT7Mp70HM09wK1WSd8YsSF/Sb0H2WgHu4n9WxOXPmjP+DHrSlcmbU/C5ongCBQSKI5rN3h+RrydVPms8XnIhLP3HjDZfH19ViMlWowo32iAScjhZTW1OlsLgycN8DHVWlv3ztDdQ7yESFFJCruwIiTnA4XNTFQz06dT3O6XQq+W+D0reenl+yF0wfae3mH7F49XCGmLy5mZmZo0aNCgsLU7j9bOUPQreQlIrVSBz2HzXEGk6Lyh718uK+rVuHm04q5atNvnjvIDXt4Z49u5f+eb2yjmjsZXUoq4jsEnrr1AzTLq5eXWTb/v+hpKpxefiTtx8LDfXVVVliiGcFnYSGmrK6Kr2gsGJSSMzcMd3HDhDV3/gfAQp9h4PfUMvFU3BIRGPmJX/HQvXpyhVXlw+1qqmpWTB/9qL+PM8172iYiS7E27FLe7Qrvv6HVFVVAZUPDg4GowdxtB6C/targWV29wz+e7R7p269TzCSZxobO0e9vnRx/1abzluJI0tTrw9wdrRo2LbkkuuFceryMxP7LK105dFHXC6vu6UhHi/OeCcg95oaDDqNvD8q5cm7wrU+dmS5jaeSG6DQdzC4WYeG9Ts36tppx/tThq4sHGlESS4t5xYWVmzbtILx5qRznM3epy9HIs5OsHfyZMRfmGkqSopIHo/n5ubm4ODg5+cntk8A+RHspP3h7ImnnoX2bMotxdGRjWmfq83XXgr3ZjScPHly99ZVWTNsdlSv9PP2koc5knsphSsPx6syaXo6LAnNzJNIeKuuBulZhT4bb4YtGUohQq3/FVDoOxgY/alHVkbb99BejKZo66o/+nPhl+wFmW+ie9q6Y6x84x7t7/Zl4m7i8VvlLg6DpzMeh48V3qsbEBBAoVB27twpxg8A+SHE7kHR13BmZCQGoaMBXjcp69Aay+p4ZB3yzJnT3dRumi3RjL12bePyIB8fH9Dv6uvry6qpTz6UrA5L0FRT1pbwDsAoFMrYUPPT58I5u+IO/DmIgINq9lPgn6ZD8SV7wfmnuz/RNPCVTdbj719fp4n9Mpo37Wq7dorTsuMnls3W3HlgVScSkmQ+92J0+eig8HcuKyyFsuq3bt368OHDhIQENFpyqe8h/4DEa3RtvRQaa+g5ndZn0iKNjZMtOXEhSz5P3HNw+1Dm50+f9u3b17Nnz/79+4NueODAgVJuZ2ZR7YpDDxnKFEmr/FcM9NTTM/MX74/fGTBA9GxIHZWOLPTFVQ3JGWVZRdXFlfXVtY3V7EY+T0Ah4ahknLoySYtFsTJQ0VGVrwXxQvM/2Qt27R/UE7d08Ky/Hi3dZ/N518JrthuWzD941WLUsVGjfJ1Jlu8OuOERSJrdmri7QlYXFRUVGhoKhF5JSZz7dUDaDEbf5/TJqiXrlwec6+q2MO7RIK0vCyQMDAy2bNmyevXqkydPAqEHNi/4t3U+ZInS2MQP3BePx2MN9KQafGVkoJH2MfdQ9OtZI62kWa8C0dGEnt3Iu/0y796r3A+fy8oqawl4LLjtsFgMeOCwGCQSUc5mNxVUc5qaV8nXN2LRKFM9lQFW2k42espKkt3mQkL8LHvB5qfJPDSu4fnRvffIjoQvls4gpylHt9z0WuTzcqFlbxNjoWtMSkry9fW9du2atra2eD4DRAgwagMXHRu46AfvkMnkmTNnzpgxIy4uDvTHy5YtA9+XFPw5u6+8Ka2ote4m/K0lHEgk0tBQ88zdtCE99Yy06FKuXSHoOEL/Mb/68LV3j1NygKQp0ylMFs3YWBPzO68C0PrKyrrjt97vufDCREdl9ihL284S34ZCXPwmewEaBz48mswkVKbk1Aosm9ObuzgYqBt7eA13fnD3rpaWlhCV5ubmjh49OiwszMbGRhwfAiIpWudDloI/J6ek7mp8mpGBukz8J1gMWkuTufHUs0OBQ6SyLlvB6AhCn5ZfvfNCcvL7fCUlYmdTbSVKOxYGkoh48NDUYPD5gqKSykX749UYpIDR3fpbCSOCUqPt2Qtwpr6rHaynePx1bNck4/Ib62cc0PF/6sw2dHJyio+Pb0synNaw2ezhw4cD2xDUK/KHgEiJ1v6cuXPngiPgX7H7c7acfUkg4BjKMnPlqbLoaR+yY59l/WGjL6s2yC2KLfQcLn/npZQr99/TaWRLc30SSXjfCzBDWtZilJRWB4c/NtWmb5zZl6Ekjf2p20W7sxeg1ccce0LZu+XoomlVRP1eQbd2ehspo5ZWlpUBrb99+3bbf+08Hm/8+PF2dnZLly4V9WNApI5E/Tn55fXP3+Z2szAUvSih+RJfr8k6ev0NFPrvUWChzy2tW3ToUW5BRWdTHRpVPLYJuFdUWTQWk/o5p2TMyugN0/v2NtcQS8miI3z2ArzOsD93D/vzf45t3rx58uTJ48aNO3/+fBu3+gsMDKytrd29e3c7Gw6RI77x5/Tq1atv377AwBfRn3PmXjows4jEdu8ZKV6UqKTsnMKPuZUm2nTZtkTeUFShf/i2aNXRBCwW093KCIsRc3gf+DHo66qCUcKSgw89HU39RlrJ1uv36tWrDRu+ZC8AP8iPHz8qKyuLXib4jOHh4W5ubj4+PidOnPjtqpb9+/ffvHlTuA1gIXKIeP05CSl5LBXZb9oF0FSj337+ueMJfX19/d9//z169GgVFWHydyqk0D98Vxx06IEai66rLeR+pG0BCL2VhcGVhE/sBm7gOGvJVfQLgLCuX78+OTl5wYIFR48eBaNvMRaORqNPnz49fPjwefPm/dpOBxK/du1aIXz6EDnnG39OUFBQy37l3/tzrly5Ym1t/cM4q6LKhryiyp5SD7b5IQQy6dbzz36jOlqcJYfDmT59up+fn6Oj49ixY9ur+Ion9C8zy1cejldnKetoS3xFBhgxmJnp3Hj2WVkJ7zu8q6Sra82tW7dCQkJycnKWLFly4cIFPF4ioZ/AfLt8+XK/fv1AXcuXL//hOSkpKd7e3tHR0cbGcvFLhoid3/pzBALBsmXLamtrr1+/3rXrtz+EB6/ziQQw0hNWTAR1xfe33rlyvaCSg1LqZOqyctBgc7ywY2gikVDDbiooq+sYexV8A5fLvdlMexVfwYS+sKJ+6cF4qhJJCirfAgaNNuukc+rOBzUGaYSdxOea+Hx+VFQUsOLZbDb4aXl6emIwkv2OgJF+584de3t7BoPxfcqakpISFxeXHTt22NraSrQZEHnge39OQEAA6ObBYC41NRW87N+//6VLlxwcHFpf9TGvUoQ4CF7N46XnIqsspx0fYUypfXPw+t+rn5ue7KMnvGWjxiDnltR0SKH/SnsVX5GEni8QBIU9AdaHkYFUQ93xOGwnU51tkS+6GjD1JZYC+0v2gjNnNmzYAKxsMIJ2dXVFoaSUi5DFYsXExAwePBhoPehavh4HnQ1QeV9fXy8vL+m0BCIPtPhzAMACCA0NBUM9KvWf276iomLYsGHHjx/38PD4en5RBfu3G4n8FG5G8uWndPeLfXpqgdtdqe9a376itp9AwHqMGFBVXixqQfIEGFT98DjQjZxmiouLO4jQX0j4/P5TsXU3I+nsVNcaMDLV0mJuOvVs/5+DxF74/2Qv2LFjyJAhYq/itxgbG0dHR4PBO5PJBP8imm+sqVOnguMrVqyQfnsg8kCLP+fevXvAZvx6ENyu48ePz8/Pnz9/fsuRqpoGof02gqpXWeUsbaUn97f+nZZVjmL2NB8daGulLkp8BYmAW7Th2PjBnUQoQ+6orq7+ZuKkc+fOY5v53pn2PQoj9PUcXtjV1zpaTBxWNm1WZdFT33++9ypnQDcdcZX5s+wFMsHCwuLKlStgJHH16lVbW1swqgA/ZmDTSb9bhcgVly5d+sac5PP5CxYsyM7O3rZtG7g96hqaSBQh/SS86iw2L+/dlWe24zd6qnKL74XE7JzBW3W2n77wS1jweEyDACuW4DT54ev4vl36/hWFEfqwG+/rGzhdOolNZNsLuKG1tVV3nXvZ10ILgxbVqfKb7AUyws7OLjw8fMyYMbNnzz5//jwMpoTU19efPHnyh28BAwWYAhEREYjmX4eQFfCa+Aic5thl1hZfArroY9aUJo19dSe1t293oRPMY9EoHu/Hjg7FBYvFBgcHt1ffv6IYQs/nC64/ygDmvGytS6oSqawEFZ+cN7CH8P1N27MXyIQRI0ZMnjx5xYoVYMDOYkkwehWiEBCJxJKSktJmwJPiZlqeA4DQBwQEkA1GNXKahCsfSWLhESQS5f/tCYwqSxnZUFbJF6HNDY1NLI0OkpX2KyQSac2aNUJfrhhC/yy9rKKa3clU9rkSlZWpt55/Fk7o2529QBakp6cfPXrU39/f19c3ISEBav1/nJqammnTpjU2NtbV1YHn4El1dTWbzQZPwKgUGF4ODg5clvKH/GrhykczuqmR9hekFfFN9L8Mk7klpRUCUheGKD56IPSqyrLfZkuuUAyhv/b4kzKNLLUolF9AppAfpWQ0NvHw2HbcisJnL5AuwEZzcnIKCQnx8fEBRr2Li0tsbCxcJPVfRklJCRgoT548+f4tMpkcHh4+duzYvVdSUrLKhayAYNVriOGJyyseaa3rYYgouvPXs2I9a38zUYSJ3cBh0duR2fC/gGII/Yv3hSym8HLDr3z09OTOly8/1vMROJaNudvyfr11hfvkWCxak6X0KCW/jUa9JLIXSAgOh+Ph4eHu7g5UHrxct25deXm5m5tbTEwM9NT/l5kyZcr3Qq+np3f58uWWuaVuxszz99KELR7Pctk/iv/X/UOjn9YjcGr2PeZu7C1CED0GjSoordVVlVQYtIKiAELf2MQvr6wzNtIU8npu+tOtcx4jxg5btlmbyi6M++v6wTk4rfN9dIQUL5aKUmp2+W+FXqLZC8SOQCAA+s5gMECbvx7cs2ePt7f3uHHjzp07B/cL/M8CboD58+c3NDR8PdKvX7/z589/HZjamqk1NXEbOU1CRtOjVQ3d9hi6iaWxCApWQCPj1RjQdfM/KIDQfyqsESAEGGEzlwnq8hrVh/Yd+WcXnS9mAnXknHdxc7I+VdrrqAo3sStAonNLan5xgnSyF4iXTZs2paenx8XFtZ7uBuIeERHh7Ozs7+9/4MABGGf5XyM/P//EiRPHjh0DQ7qvQj9jxgxgAbQe5AEj2tyQVVpWraUhTL4t8VJdVTO4pzzOfskWBRD6nJJa4dfdIRBImoPDnH9XbPNrP9dwqUwWWWjRQqLQJRU/EHrpZy8QF6dOndq3b9+zZ8++z1wIfs/gQzk6OgYFBW3YsEEmzYNImcbGRvClA31/8uSJu7s7GI/W19cPGjQI3M87d+6cPXv295eM6W+8OfKFzIUej0W9fl/i72oh22bIIQqgRMWVbLzQ+ZK+ofF90pHQqs5/upoK70hBoVHFlfWtj8gwe4HoJCYmBgYGxsbGqqn9eENn8KGio6OB1jOZzIULF0q5eRBpkpycfOTIkcjIyG7duk2ZMuX8+fNE4pdZTWDEWFtbb9my5Wdp6x27a4ccf8JmN4qy+Y/oMAgIZQrBQAOGD3yLAgh9bT0HLY6M87zS2/d3B7+nzho7ewxNhPLQWEx59T/DWHnIXiAKmZmZo0aNCgsLs7D4lRHUkgzH3t5eVVV14sSJUmseRDqUl5eDUR24k0tKSiZPnvzixYtvYn+B4fL48WMs9qcDawwa5T20y/kHGV276Em+vT8Gi0Y+fZ3tP7qjJSgWCwog9GQCls8XcZ0bv+HDgcu7/uY5bJzk3p8iWq+BRggoRKxcZS8QjqqqKqDywcHBzs7Ovz1ZW1v7zp07/fv3p9FocMPYjgGPxwMjOaDvt27dGj58+MaNG8G47WeD0V+ofAs+zuaX4tPLymtUGLLZNlYJxVVTJokxQ0lHQhih5+ad9ug6Ickr7uXugcotd4Wg5vESa/v9RkffRE3Vwzblx24IWLTnSkopD6Fk6Dj1rwMbJ5gIHdeqziBzhF131wy/MS303PYoutffTv30MaJPKAr4xa+v6uhMA/a7/GQvaC/gR+7m5ubg4PB9auKfYWJicuXKFdA3AK3/JlEtRLHIyMg4evQokHg9Pb0pU6YcPnxY9NUSaBQyeLLt0oMPlekyWPKiTsPdevju0KKhUq5XURBG6DFankfO3u821DNgyJuIkapoBL8ibonnliqvy8cm6WERjW82DnNai/ALjz/Xj1XzdP8MLy9npa5v1lkK6bzrpEVr5HCFu/YLdU/uhh5rcgjta06oryhsOYbEMyhkIcMrcSgBEYcEP4y7d+8i/j/Dn5GRkfAtlAUBAQEUCmXnzp3tusrGxubkyZNjx44F1v2vvT0QacGtq6xDKdGIbRin1tbWnj9/Pjw8/MOHDxMmTADmvHCJU35G7y4atl003mUUmJpoibHY30IhYN59yBnjYCq5LOKKjnCuGxRj8NaLwY/sJvkMfXPZGx8zd8JB7Ly7e13VwM3Gq/hUaeKxftXWiVZfjHj94JCT+5xjn5autdQSrpfXZlGA+cnnC1AoYazxptzrmTWChluzw2/9exBne2jmrF7ChfIgBYKRE/wWjQ/LycmJi4sDkrd27VoMBgPk3rEZDQ152U/8Z2zduvXhw4cJCQlCRMeDD3jw4MGhQ4fGx8fDPadkCrcwdvVE3w238/gI5qB10ReW9ab98CcmEAjAlwX0HQzI+vfv/+effzo7O//WFSMc63ztfTffyvhUYGQgpV8BHoMqLSwGKjHdBVoeP0VYHz2S0nP5hR33u83yWJ7FOHxWa83T9f1pzTqMVnfZdtHl64ncsrScRuWuhlShx3JIJIKlTK6uYdNpwoTKYDut8w9fJ2zlP6CsotbG5suMk46OzuRmwHNgIgHFv3jx4ty5c9XV1VtEf8CAAXQ6XYxVi4WoqKjQ0FAg9EpKQvpSR48eXVJSAsQCjGm0tKRqu0G+ws2OmDD+tMmRdPZI1c/ntl4uq+UhvhX6lkD4sLAwHA7n6+u7adMmSaffwGJQ+xY4TgyJyc0v1daU+DZwBBwawa4R8AXBk+1QcJ3HzxFhMhZn4vf34ZtmXqtqrbenLbb60Uo0Qe3LHVOWZwzadqGfSPMztl00n6eXCif04gWDQr77VPqXj903xzs14+/vz+fzX758CUT/wIEDoA8wMzMDig90397e/vsodemTlJQEfvDXrl374S7PbWfGjBnl5eVOTk5wx3AZIah4dPxll9WnRhkQUQizcauWtnrvm0D4iIgIO7tv71jJQSFiwxYPnboxNieXr63Fktw6OyoRU1NWXlXbsGvuQNDBSKiWjoEoUTf88uQ7SWyiEvLdxZgsfxPTb3zwjVnnF46cEqm2Ou78DEPRhonjHE1iEzONpTUY/AVULL+zHoNB/emuCCgUyrqZxYsXczicxMREIPpr1qx59epVz549Wyx9Gxsbmaylys3NBcY4sO9AA0QvbenSpWVlZUDrb9++LQ99WAeHV/Xh9qnDx190Xbd/igH4OQma2I0YZSYJhRA0FKZl1KuZGtCxXzry8PDw7wPhpQz4gRxf/sfKsEep7z8bGmgSCOLPlaSmhHnyMrOHqeq6afYEca2z6bgI/wfiZp+YOuG03tanEcxl1j5jN/Z7vKr71187v/zBaheXHZzpkckbRmiJ7Aw00aLTKPiq6joaVcZGfVl5zSDrti6wBuPlfs2sXr26trYWGL9A9OfMmZOZmQkOAtEfOHCgpaWldFILsNns4cOH+/n5iTE4cvPmzWDUMm7cOCAoMPGZZOBVf4w7feTgwbDLaYxBk2b69fwngy+KamiCz07JePZ28fCVr6imxEZ2PQpDQLCn+/p+HwgvfWhk/K6AgWfiPhyMfq2no6qiIrZhHwWPIQga7zzK+NPTepiNvriK7dgIK/T1b3d4zHpgtzdlTlc91OGjV83Hui93TNre74ufnl8Zv9zR6ZjR7ucnfToRxSRi7g6mp+9+tOgiS6FXp+JiXhWtntJbiGspFIpTM+A5MITv3r0bFxe3f//+iooKIPeSDt3h8Xjjx48H43dghouxWNBFAfvRzc3Nx8fnxIkTMBmO2GlMWd2z+37VKYHLbuwd2VOtdV9KthjTrWDBpPFUgcUwbtL9/sPssEmPc5YlL5+qKyf558DtMG5QJytj1tbI5+/efVJXV1FWVhLlJiFiUXgBJzH5k4mW8pElQ3VUZROwr4gIJfSCqocrRi9Ndz37ZrLeF2tdffTek1MsnD3mD3kd5sysvDVvzKba6dc3DCGV5ua0XIGmqGoo40WRgYlDzSLjPpRX1DCUZfPtgvszK7tw0h9dqMLGZX5FRUXFvRnwXDqhO4GBgWBIsXv3bjGW2QIajT59+jQYK8ybN08S5f+X4TdxsUbOgwxvm68IHKv/Pz/VjIyMw4fvPa79XF5vuHmR84yLETQatfj0kAEJBZypunKVi72zHiNsydDnH4rCrqa8fftJX4eJIRAI+Hb8iFBIpAoJVV/HTnyZa2HE2uLXv7Oe7LOnKRZCCD2vKGrOmO3saTf3j/7/vdpRzD+2n54TN3DCjKFvj2n+HV0iqNjl1GnXv9dQx8XlnR4oyu5eGDQqyNtmVfhjOo0iXJyliGhS0Q8/1k4YLOaFQlII3QHjhps3b0puA1gSiXT58uV+/fqFhIQsX75cElX8B+FlH3YaX77n3uwJ/YqXxOT5+emhOOVpn2ofPIo7eeyfQPi4U7MmzMrVG+lL+5LTg8uuxHYdbCz8ptqSpGcnNfB486n0SnxG/OscJAqlrUajUEh8FBqJAtbCt1OpWBSw35EoAa+krOZjdhkOi+5vqbV/4WCYx0Y4hBB6tNrIE0XfpiRA0gfsyRLsaX5+vFxwXPSWfY+DlZaZrnJOXomejrR3aGJScPHP0xeOs8aJI+vOz5BE6A6QeDBWkHRsDCgctBY0j8FgtH2prSjU1Dc9SS1+l1VWVFlfVdtYW89hNzQB049MxNKV8CwaSYdFsTZhddaT351evkdQ+zYyLKXHjHGdiAgkDt9Y+rmiidLNy64g+MYZYsrCmfuKuEgSkdpz3LLkm7fV8FhwwfGUoc6Dp3xaMkI199quo4y/HivLs/usqwETPBAI28z8qsR3BUlpxWmfKypqGnh8AZWEo5Bw4BusqmusrmsEPzQWnWioSXew1Fzk2QN6aUREwWar10/rM27NtWICXpUlvY4dj0FlZxfYd9XsayGlmHFxhe6kpKR4e3tHR0dLYWVTS+KzwYMHA6339PSURBV8gSDxfUnss+zkjOKi0hosBk0i4fE4LBaLxmExJAoOiUQ2cJqyS+ozCmoeJOcdjEpGIgSmuirARHC20VehyaexixDw+YiWUWpd0u75kyqLDJ+F2FCIKqS63PSc/HsPcKVP/H1e0scsWL/9Tx8WPnOt46iJZ7xiJmmhkRTrFXHP7I/uiYh8LDALvBg0gqkYUYaGmjTwGD/YrOVlYxMPyH1lbaNAgFChEkBXLVGL6j+Iggk9g0rY++egaZtu4nAY6YTV47GohspKEh6z0NNaCtV9j9ChOyUlJS4uLjt27LC1tZVOU0F3AjoV0CQmkwn+FWPJdQ3cMw8yL97/UF5Zp0yj0OmUHlqstuxSUN/AqaysPRX3cf/lVxZGqvPGWHWRN/duXeLiPv7ofXc32FORZC19TfUXRyctHfSgf/7zlPKHs3pbeHm47po7HT99+4TOpObvmOW3wOzk3U8Nk7S+/ACQBN1B/lsG+cv4U4gGHotWZ5DBQ9YN6bAomNAjmkMt98x3nLvrrrGRpqSjLYk4NKK+tpbduHveQJlMDHxD20N32Gw2UHlfX18vLy9pttDCwuLKlSuurq5Xr14VSwfT2MQ/evP95ftp7IYmHU0VEyPtdn0RRAKOqM7QUGfwePyCwvIZW+4Ya9P/HNvD0kjiizbbCrlX0A773uNn9XpyYgyDRSYQ8Wq8/UP1HvWxtKSRe1x7s67HN4NXbmVek1F/Q7macYXIOYon9ABLQ+YWv36LD8RraKhoqDEkVAudiMnPKxIIBNvnDJDDFRm/Dt15+/atlpbWihUrpN8wOzu78PDwMWPGxMbGmpubi1LU66yK4KOPy6vYetpMFpMmSmQeGo3S1mJqaqgUFlfM2XV3QDftFRNtcFh58A+glAdsPDjO3rW/xwrSh9K8bFafueE6Z5byxjhW7C1gN994/JLoqYN3GW/aNJz86WZo8DHzXY81FMNHA5EP5E6/2kgvM/UTy50W7X+QkZmnp6su9I6yPwTIiRYNc/vJR+feBrNGWqHlwJb/Nd+E7sydOzc9Pf3jx49du3aVSdadESNGbNq0CYw8Hj16JFyuBb5AEBabdvz6awadYm1lJK7hFChHU52hxqK/SM8fu/raroABss132CojfFYn3IciyxX7jPdt7fvn+LHOCT3cTxVzLSqaE3SjWENXB8fPXux2kK1m67n26orBcj3nCpE7FFXoEc1ZLSOChoVeeHU98ZOutipdtLUYX2FSMDUVVXcSi4Mn97btIvukC+0lMTExMzMzNTUVmPwyzLrj5eVVXl4OakxISGCxWO26lsPlLw1LfPI628RIg8kQvxAD697MVLugqGLy+hvBU3oP6iGDRaSgPwbjnhMnTnzNCE+uvebRY8Euc0LF+yKe8qDNxybeGBBamlvNQ9CBFYM3GLP5+pjN0m8opEOgwEIPwGHQf3paD+6pu+9y8ps3mVqaTLoyVWjrT1UJU1xccTu50NXe6FTwcCpJ8db0x8XFBQYGftVW2WbdCQgIKCoqcnFxAUZr24M7gcovOvw46V1ed0tDAl4iqXRb0FBTVqIQ1x57gkEhHaS1LVHrjPATJ04E3wjogP95jzbucMRdK6cjJcTCRgSS1n/D1UjrAhsWdNFAREexhb4FSyPWgYWDUzJLw6+/TU7JMNBWQeNwBBIB07Zk62QcAsPj5pdU3UmpcB9gumqSrehrX2VCeno6sKMjIyNNTEy+eUtWWXfWrVsH7Ho3N7eYmJi2LNfiCwRr/0568S7P0lxfoirfAoVMMOukuzr8yWY/bC8zdclV1LaM8CiVYdsvrspYWEH4snUmkmLhOQVmWIeIhY4g9C1YGDK3z3HILam99zLnybuCV8l5agyyGlMJWKyCL2vvUFgs5kvGaoGAz+ehkQikgF9TW5+RVwl+hradNdz7G/ex0CLiFfUPUlJS4uTkFBISAuz0X58p5aw7e/bs8fb2Hjdu3Llz59BoNND9nTt3rl279ocnH7z+Pu5phqW5HlEC+Q5/CNB6Q0PNxfvjjy4dKolVl/n5+S2b9pFIpKlTp/4mIzxSyWZ1XLzYGwH5z6OouvYztFkU76GdwYPTxEvOKEn9XF5Swa6obSytqq2oaWji8pVIOIYSgU7BK1MJtqbMBWN7dIDtxzgcjoeHh7u7u4+PT7sulELWHSDuERERwID19/cPDg7+448/3r596+np+X1Azrvsqr9jUjoZa5FJUl3ZRKeRdXRUlxyMPx08XFwT799khAfDrJ49e4qlZAhECDqa0H8Fh0WDwbhEx+NygkAgAPrOYDDWr18vSjmSy7qDw+GA6tnb2wNxr6qqQjTnNwbq3/ocHl+w7uQzZWUKQ1mUlEhCwmLS0itrzt1LG+fYScSiXrx4AfRd5hnhIZDWdFih/++wadOm9PR0YIyL0cMu9qw7oOfIz89vUXkA0MGNGze2HitEPcnOyivr2U1me6xrarEORb0e0lNXhSqMLpeXl586derQoUNsNhv8oeQhIzwE8hUo9IoNEJd9+/Y9e/ZMQhGTYsm6s3PnzpUrV9bW1n49AooCzf7rr79aXgJzPuzaa11tJhYrsxuSRMRrqSsfiU5Z4tWO7bdaBcLfGj58+Pbt28HfBOblh8gbUOgVGCC7gYGBQGjU1NSkUJ3QoTsxMTHAzv3mIBgiLF26lEz+ksQi/m1RWUWdqbFI29iKjrIK/fqTjLnuPdoyJ//+/Xug760D4eHeuRC5BQq9ogLkddSoUWFhYRYWMojBa3vojkAgSEpK4vP54DmRSKyvr28pobS09OjRowEBAeD5pfgMpgpV5oYwGE9osKgPX+cN6aX3s3NaAuFBy9PS0oC+/08gPAQir0ChV0iqqqqAygcHBzs7O8u6Lb8J3TE2Ngaa3nImUHlwEI/H19XVgZe7d++ePXs2X4B8m1msq92+1bMSgkaj3H6R/b3QfxMIv3Dhwh8FwkMgcgoUesWDx+O5ubk5ODhIZ4uPdvF96M7Bgwdbn8BtRlVVFfRV6enp0dHROl37sus5Qiad5n1+FjwqPr/1IaP+myJ7qgp5YxPIpKcpmRwu72s+9NzcXKDvERERbQqEh0DkEij0ikdAQACFQtm5c6esG/IbWkJ3rl+//vr162/eKi4uRqPRFhYWW7dunbDYWIlCENJvw6urq0cxRh8d3Vftn1QBSCyBJvxdjcGgaRR8em6lkQblayC8h4fHmTNnrK1lsyEBBCI6UOgVDKCMDx8+TEhIQLctwYNsAcb7gwcPWh/BYrHKyspUKpVMJhMIBCKR+C4ts11bRf8Pgjp2A5KkqU9jiG0ilE7BBwctvn8rCgbCQzoMUOgVCWBjhoaGAqFXUlKMLTQrKirc3d3r6+vZbHZtbW1ZWVlpaWlJSQmw6MG7QOsjIyOvZSjhcU1CVsCrYzfy6xJDIs8mFlfwCFq9LdwW2ViqidIHEol4qkHnFy9WwUB4SIcBCr3CkJSU5Ovre+3aNeEyvMsEFouVmpr65MmT799SUVEBn8XW1vZUyM225Dv7IQIOG0UmC3jGPaZPZ+JKc25tvLNjWtPKs6Lsv0Qk4IysB0OVh3QkoNArBrm5uaNHjw4LC7OxacdyHnlgwYIF3+8Vrq+vHxsba2pqCp5zmrgUYX0jSLqz2+6vcUcmjMmbqj+MT45NsfOzETogBo9D1zYIO8KAQOQSKPQKAJvNHj58uJ+fn6urq6zb0m5GjRqlrq5eWFj49YiVlVVMTMzX/AdEHIbL44mnMqymugriWXkZV4DAChuUz+PxydLKnQmBSAco9PIOj8cbP368nZ3d0qVLZd2WdvPp06fQ0NDq6uqvRwYOHHj58mUq9d+MoXQqoaiSI1z53NyzD26WGXvM1KU0B91wcvNLEIQuahgRll41NjYx6ZLaiBgCkQlQ6OWdwMDA2tra3bt3y7oh7ePevXugzfHx8T4+PgkJCfb29vX19Z6enhEREXg8vvWZGgxydkmdcLWgyeSqpxuu1dFGeAxTQRdkXQtOKjeyHdpVlIVMDY1NanSJb7UIgUgTKPRyzf79+2/evPno0SOhpyulTGNj46lTp3bt2sXhcObNm3fy5MmWbGve3t7gyfbt21Gob7fGM1Cn3k/OFa46pLKT85Lae38fvbh0Cw+BJukMtF+0tJeOSH+riup6VWUo9JAOBRR6+QVI/Nq1a4FRrBDZsgoKCkC3dOjQoR49emzevHnIkCGt10Bt27btZyGhA7tphV5MEggEQq2ZQuENPIet8BwmbLO/gYJHl1c3GGvTxVQeBCIXQKGXU1JSUoAVHB0dbWxsLOu2/Ibnz5/v3LkzJiZm/PjxDx48aIml+YZfBP6rM0h0CqGqmi1kFgTx0tTY3UQVj1WAxWgQSNuBQi+PlJSUuLi47Nixw9bWVtZt+SlcLvfixYu7d+/Oy8ubM2dOaGiocPtPAfp300l4WygPQl9UUjW6n8w2P4FAJAQUermDzWYDlff19fXy8pJ1W35MeXn54cOH9+7da2houHDhQldXVxHzMUxwNImK/2hsKJz3RmyokLFJL8v6WfaXYRsgEEkAhV6+EAgEU6dONTY2XrFihazb8gPevXsHTPizZ8+OHDnyypUr3bt3F0uxOqpKhlr0gqIKTXVZxjU2sWsHWeuSCDD5MKSjAYVevggKCsrPz79z547Md+FoDZ/Pv3Hjxs6dO9+8eePn55eamir2Pa1WTrTx2XSTxaRhMbLxjzNI6LuPc06vkn1+fwhE7EChlyOOHz9+/vx5uQqmrKmpAa0CVrySktK8efM8PT0l1DZTHeWBPXRfZxUbG2r8/mxxg0Ej8/KKvYd1ZsEIekhHBAq9vBAXFxcYGJiQkMBiycVeSy2LWiMiIhwdHY8ePdqnTx9J17h4nPXIoKiqajaNKm21VSchP1XWew/pLOV6IRDpAIVeLkhPT/fy8oqMjDQxMZFwVYK6zNvhO7ZH1s+NOuzE+JF/qPWi1qSkJKnlcVQi4UKm2y87lNC5ky6JhP/9BWJCi4a9Hp+6Z74jBv3tYi4IpGMAhV72lJSUODk5hYSEANtZgtUI6j/fi9i5ZdvhB4J+0xauXTFA+X9V/meLWqWJnbnmn57W28+86Gquj8dJY1JUnYqNeZi6fkZfM12Y3wbSYYFCL2OAqnp4eLi7uwPzWZL11CX4d3a8Yjw9aF/yuUFG5P8xXX+9qFXKuNobllc1/H37vVknXRxOsvenLgMf+/D9Qo+evczUJVoRBCJboNDLEoFAAPSdwWCsX79e7IXzagtzytHq2izCF1UndR5uo/V57Er/IWqtRL4ti1qlzxSnLlgM8vDVN4YGGsp0iiSqAB2ZGglx7f67Pz2s/7DVl0QVEIj8AIVelmzatCk9PT0uLk68FjQnN2ZjwJ+bL6c1ofiILvOu3t0+hIli9JtpP2/99QL3qVqCsvSXBy48irpyrrhA1EWtEsJrSOcu+ipLD8az6+o1NZni/fvQSdia8vKnGZWh8x1NdZTFWDIEIp9AoZcZp06d2rdv37Nnz8TrChdU3J7dx+vd+KPPq1zMSAWRHr3m7Zn2ck1XPM1uxsCcwFNJbx6O33n1M5lKZhDo1n+e8llgT5fLOcjuJqpn14xYGfYoLS1bTU2FLg7THo9B0XH8x8kZ3YxZEcudSHh4/0P+E8AbXTYkJiYGBgbGxsaKfeVR7fP9Ucw1ietG6X/5brWHjO+yLKqsCYHIeJd9vJz4YknvT4Z2Z+PPjrHvwS+/NbP7+OX9Uvf1ltPgcRoZvytg4IPk3EPRKakFpZoaKlQaRTjrXomAwfAan77J0mJSgibaQKc85D8FFHoZkJmZOWrUqLCwMAsLC/GVKqjPSXqPt7K0Drl7VV/vyxfLK39+dMGqT9rD3o8cEpL69o3f9LHbjb1tli6yY3yx4VGMPj7OpDUFjQiEnAo9otmZ7tBNGzyevCs4eu1NyptiXQ06Bk8gEIFy/34NLQGDxCG4VdV1CSnFFgbMkOl9LQyZUmg2BCJXQKGXNlVVVUDlg4ODnZ3Fu9q+/lXIhBUDHt4eZ9al+XVNTeXu7eGX88vRB2eje8xOyriqS2xe1CrgC4CAgie8irQcZn8z2eeMbAu9u2iAR1Zh9eM3+YmpBa9e56kqkxl0IhaLBYqPw2KQKBQei+Zwmvh8PoLPr2/gFJXXlVayrc3U+phrLBzbQ4slkXldCET+gUIvVXg8npubm4ODg5+fn1jKK76zbXuGU/AMCxICyzRSKnlbyEGw8lstao25tsXegj/HyivkRcjBvjhE06f9TkOvOIQEdKlIOLH9b+K6RFN5SbfQFvTVqeAxfrBZE5f/Prs8LaeioqahoqaxorahuoZTzRcwqAQmBU9XIqgxSODMLnoqKJQcZQ2CQGQCFHqpEhAQQKFQdu7cKa4C69+f3jRnb5VB0t4hKiqG9PydN8a6rXr87aJWjv9kmnt0ekPfbgSs/pT963OW7/3rBqmL08bbf45SV8w9NrAYlIUhE/phIJC20GGFvoHDe/6x5FV6aV5ZXUV1Qw27sb6hSYBAgNE9hYRXoRJU6URzfUY/Cw2ytNLSbt269eHDhwkJCSJmb697unzYMtKuK0HWFLRKly7aeu+vTZ7c9OeopwdfVue+6b19TeS3i1oFSDyOiMU3B9cgiSZj158dK9IngUAgCkVHE/qP+dVRjz49e1+UV1zF5/OpQNTxWBwWg8XhqHQiGMVzefw6DreysOZ9TmVM4qfVRxtUGRTrTmpONnq9OqlJbkFoVFRUaGgoEPpfbKrXRsg9/1xl1mf0VL2Hp7wRBBNe1Zu6ppsn1n3cGuJ6eCtuwOSZX0SeV3Bp9qRzOpPHmtYlnd+771mPIwkK5aOBQCDio4MIPY8vuP0q/0RsakZ2KZVKUqaTu5q1KTEW6AyqqtmvPlXcTcrGY1AThnaZ4GiKxYg5sDwpKcnX1/fatWva2tpiKA6lMmTbpbF9+lhaHUcVPlHmkGZHX9fYOmH9I5pKzatctgBBQiLQao7TxsSuDF1/XcXKacW9Q+4WNLmMlodAIJJH4YVegEDcfJF7+Oqb/KJKdTXlnj2Mgf3e9stRKJQynfJlnb2eWlV13d+3P0TEvPEe2tl7iBlOTDtg5Obmjh49OiwszMbGRvTS/t2ptQRrWpNAWXyk3+llWXj7pcfCHvQYFVFu9KaQ48EEPRyK1nPWgZhZotcIgUAUHcUW+vIazurjT5+/y9PSYPTqYdKWwOpfQKOSLbqQa2rrz97LuPQgfbt/fxOR18ez2ezhw4f7+fm5urqKWNT3O7U2vtnsOGDJDWYN6kMlss+I3WcXPu4b9qmMi0BIL8cvBAKRfxRY6J99LF119HEjp6m7hQGBIDb/sxKFaN5Zt7ik0mfTTb9R3SYM7iR0UTweb/z48XZ2dkuXLhWlST/bqZVktfjiodfdPCKRiVkNPppU+5Cn+UEkdcWIi4dAIFJDUYU+8n5m6Lnnqiyamam2JHLqqrLoSkqkozFvX6UXh0zrI5zXPjAwsLa2Fmi0cG1ow06taE33QzFbsPtJLelqsDR1unB1QSCQDoxCCv2pexl7zz83NtBgqlAlVwuRgLMwN0jNzFuw997ugIHtXXezf//+mzdvCrcBbDt2akUqWQceP9LeCiAQyH8JxRP62KS8fRdeGOqpS1TlWwDibmKklfohO+Rk4spJvdt+IZD4tWvXxsfH02i0dtUo/Z1aIRBIh0fBhP5tduWG44+1NVVUWe0TUKFBIpFmpjqP3ubsv5LsN9KqLZekpKR4e3tHR0cbGxu3vSJZ7dQKgUA6PIok9Bwuf1X4ExqVrKWhIs16USiUibHW2btpfbpqWhqxfn1ySUmJi4vLjh07bG1t21K4POzUCoFAOjaKJPRhN9MKS6p7dm+HmSwusFiMro5qyImnp4Odf+GsZ7PZQOV9fX29vLx+W6Zc7dQKgUA6MAoj9BW1nHO33xnoq6HRslnhyVShZVTUXIxPd3cw+eEJAoFg6tSpxsbGK1as+HVR8rlTKwQC6agojNCHXnkDDF5VppRc8z9EQ5N1KOq1s60+6Ud50IKCgvLz8+/cufMzw/zfRa15crpTKwQC6ZAohtBzuPwHLz/rass4Jy2JhGcqk+Ne5oywM/zmrePHj58/f/5nwZTfL2oVMYElBAKBtB3FEPr4t0V19Y3K4tgeWkSIFPKtZ5+/Efq4uLjAwMCEhAQW69up2p8taoVAIBCpoRhCH5OYpaJMlYe5SiUl8svk9Bo2R4n0j+Wenp7u5eUVGRlpYvKv774Ni1ohEAhESiiG0L/JKNYQPqRSwMmNfnj66Pu0zw1cJF7dpovLkr52Bliheg00GmWgqfz4bcHQXnqI5mBKJyenkJAQR0fHlhPasagVAoFApIICCH1dI7e8ss7MVEfY6x/d3rjqs+l8p+DBTEJ14d111w77ozQvO+gLmeKRpkRMySwFQs/hcDw8PNzd3X18fBBwUSsEApFXFEDoM/JrgB0tdFQln0fQGRHcre9ITQooQUtpxAyd2PkFhXUIYYUeWPXFFWyBQAD0ncFgrF+/Hi5qhUAg8owCCH1eWS0eJ/y2riiqtcUf1i3PBfW52XdOFGB69DUUIU8OClVcxt60aVNaWpqvr2/37t3holYIBCLPKIDQF5fX43Eit7Mh8erCWWlsBEK5b78lG6xUhS8QhcY8v3vxYmIkHo+/cuUKXNQKgUDkHAUQ+sYmLlr0Xf3wlgNWnu1ZkZmTEPZ4kx8/6JCtHlG4krAYdP7H587OzmvWrIGLWiEQiPyjAEJPJeO4XJ6opSCJFHUT8FA37YLMcn0cndx9Tm/homGQCIG958rTG0eJ2iQIBAKRCgog9BoqZA6nSdirBY1v15wOL7NZvquLcvN0LhKJQiL4ovQcAh6LLuRoAAKBQKSPAgi9mQ69kcMV9mokTtteuW7JvfAIoocTi1hT8mTXk1yywajOQk/v4lEIVWU46QqBQBQGBRB6NTqRx+ODh3ARlkja4D+Wrog/ffTqyt1gXIBhWJlNOuzQgyH05CmPy1WDQg+BQBQHBRB6gI46raq6jqGsJNTVKLzemMFLxwwWU2PKq+oGWsogJz4EAoEIh2IIfR8LrbhXecIKvTjBY5AvPpXZ+fWXdUMgEAikrYhX6AU1KRHLFmyIjE8r4yDppoMmrti9wbszWeQQ8wmOJufvvhcIBDIPVyeheL3M1Mk/ykcPgUAg8ok4hV5QfmPWgKm3+m0+8dTdglqRuH/m+EnDMJ0/bO8paoyKOoOsoUIpq6hhMkRY0SoyoJPJzi936wf9NhAIRJEQQui5n48O7+pX9VfKg/mmOAS/JHpil9FJMx4/X9e9iTQw6LD/5Kl9mGgEwkA7KHjADtfEtBpBT6LodvjkP7rsvpAsW6HXoGJSU2sG9hA2vRoEAoHIAiGEHqM3KWz/pa4zZ4SPvD2ddnfpzPOawU9X9CIjEWSHaQsdWk7iVWfcCd32BNdvg62yWLwtLnaGx2LeFRVXqqnSxVFeu8Ggka9Sc/xGWeGxcHMoCASiSAjlusFojz906JLFDL/9SgbbIrXWPl1s1co5U3PbQ3fIuUoEQtt5091TfkbicWcjkYg1U3vP3hGnoqKEkcU+fCp4QQkaNbz3t5sIQiAQiJwjpI8erTFm3+GLnd287thse7PAnND6PbLdjievF+W9u3s8ZNWAoZyEuBXdyeJoKsLCkNnPSjvlU6GJsZZYCmw7GnTczfjUXXMHyHoyGAKBQNqN0JOx3LL0zDrwX+7brBp+J5VWS5lQZK1OFuDRq5816rnJ6nWP5l0YIq64yBUTbcavvZ6TV6qjJb2NwpUI6GevMicO7dxZT+hdriAQCERmCCn0DW+2eQcX+sQ8Mgh2nDRvVMpxF1WUoPKWr930oqCEqIlaza4VJAqDQnA5XIH4mkvEYw4vGjx5fWwhBq2upiy+gn8KhYjO/VzYy0x94rAuUqgOAoFAxI5QQs9+tWnCmuKJ19YPsyPqBEd2nzJ71NtId3Uliz9Myz3nTdvC3DzBilaVfGrJ2hSq82prilhbzKKTDgYOnrIhFo1GsZg0sZb9LcpkbG52gYYKaaFnT4lWBIFAIJJDCKGve7HBa12J19WNjl/iacznH1txqse0mWfsLkzQcj9+/+Di+Rs8LJfVAutbx378vrjto1SF3APw5+ioKh1ZPGTOzjg2u0FHWxWFkojjXJWCfvHmk6Uhc8kEG+iah0AgiosQQk+2/utt019fXxItg1O4wf+8oHWfcfD+jIPiaduvMNCgRa4avubYk7fvPxsYahIJwuWW/zE4DIqB4916nDbXvfsIOxhmA4FAFBvFyHXzQ5RIuK3+/S8++Lj7wktdTRU6g4bFivpxgOWuRsF8yCjIa+IdWjREX12W67MgEAhELCiw0Lfg1t/Ezlzz+I23MU8zgdxTlanC7SQOrHhlgiA1vTCjpmGykzkw5DFCZUWGQCAQeUPhhR7RvAXVEi+baS4WJ2+mXnmYoaZCUVIioXEEEgn/22vxGCQOwWPX1b//WErEYyb9YT60p56EnP4QCAQiEzqC0LegQiXOc+8xw8Xy+fuixNSCJ+8KKmoatVWpFBIOhUbjsRgsDtjoSIFA0NTE5fP44N/yanZ2YXVXQ6ZtFw1fpy6ddKURrwmBQCBSpuMIfQvAKu9npQUe4HlxBft9dnlheR1Q/MraxtKq+gYun0LCqtMIDCWCCpWgo0btrMeAuWsgEEjHpqMJfWtUlUlwc1cIBALpyEIPgUAgEAQUeggEAunwQKGHQCCQDg4UeggEAungQKGHQCCQDs7/AWMDkX+ejJzQAAAAAElFTkSuQmCC" alt="" name="图像1" width="387" height="180" align="left" />
|
x1 |
x2 |
x3 |
w14 |
w15 |
w24 |
w25 |
w34 |
w35 |
w46 |
w56 |
b4 |
b5 |
b6 |
|
1 |
0 |
1 |
0.2 |
-0.3 |
0.4 |
0.1 |
-0.5 |
0.2 |
-0.3 |
-0.2 |
-0.4 |
-0.2 |
0.1 |
同时,我们设定学习率l=0.9,实际输出值为1
import numpy as np
x1 = 1
x2 = 0
x3 = 1
w14 = 0.2
w15 = -0.3
w24 = 0.4
w25 = 0.1
w34 = -0.5
w35 = 0.2
w46 = -0.3
w56 = -0.2
b4 = -0.4
b5 = 0.2
b6 = 0.1
l = 0.9
t = 1 # 定义activation函数和倒数
def logistic(x):
return 1/(1+np.exp(-x)) def logistic_derivate(x):
return x*(1-x) # 正向更新
z4 = x1*w14 + x2*w24 + x3*w34 + b4
z5 = x1*w15 + x2*w25 + x3*w35 + b5
O4 = logistic(z4)
O5 = logistic(z5)
z6 = O4*w46 + O5 * w56 + b6
O6 = logistic(z6)
print(O4,O5,O6)
结果:0.331812227832 0.524979187479 0.473888898824
# 求取各个神经元节点误差值
E6 = logistic_derivate(O6)*(t-O6)
E5 = logistic_derivate(O5)*E6*w56
E4 = logistic_derivate(O4)*E6*w46
print(E6,E5,E4)
结果:0.131169078214 -0.00654208506417 -0.00872456196543
# 反向更新权重和偏向
w46 = w46 + l*E6*O4
w56 = w56 + l*E6*O5
w14 = w14 + l*E4*x1
w24 = w14 + l*E4*x2
w34 = w34 + l*E4*x3
w15 = w15 + l*E5*x1
w25 = w25 + l*E5*x2
w35 = w35 + l*E5*x3
print(w46,w56,w14,w15,w24,w25,w34,w35)
结果:-0.260828846342 -0.138025067507 0.192147894231 -0.305887876558 0.192147894231 0.1 -0.507852105769 0.194112123442
b4 = b4 + l*E4
b5 = b5 + l*E5
b6 = b6 + l*E6
print(b4,b5,b6)
结果:-0.407852105769 0.194112123442 0.21805217039
四、简单神经网络算python实现程序
介绍程序前,首先引入一个矩阵点乘基本运算
import numpy as np # 一维矩阵 a = np.arange(0,9) print(a) b = a[::-1] print(b) print(np.dot(a,b)) # 二维矩阵 a = np.arange(1,5).reshape(2,2) print(a) b = np.arange(5,9).reshape(2,2) print(b) c = np.dot(a,b) print(c) 结果: [0 1 2 3 4 5 6 7 8] [8 7 6 5 4 3 2 1 0] 84 [[1 2] [3 4]] [[5 6] [7 8]] [[19 22] [43 50]]
在实际编程过程中,引入7,8节点来代替偏向的作用,省去了计算偏向的过程,此时所有其它节点偏向为0,简化代码编程实现,下面式代码实例:
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfUAAAE0CAIAAAC6nj1XAACDcElEQVR4nO2dBzzV3xvH797u5dp7jxIVpSglSSESDe3SVCn90kJEJE1pD2n92kuD9k5pqzRRyd7zWnf8T/z+fn6Srruvzvt1X3Xd+/2ecy7f+znPeb7PeR4Mh8NBQCAQCKTTgRH3ACAQCAQiFKC+QyAQSOcE6jsEAoF0TqC+QyAQSOcE6jsEAoF0TqC+QyAQSOcE6jsEAoF0TqC+QyAQSOekk+s7k8VOy6n8ml+ZW1xdUllbUV3H4XCIeKyCLFGNTtJUohhryOKxaHEPEwKBQARPJ9R3NofzKqPk6tPM1+mFWXllLDYbh8XicBgsFo3FYFAoJIvFrq9nNjCZ9Q2s+voGBTlyd32loVZa/UxV0SikuIcPgUAggqFT6XtxZV3c1Y/XnmRUVtXSqCQ5GqVbV20SEd/OKWw2p6KS8T6rPCn1cV1dfV9T9YUePbRVZEQ2ZggEAhESnUTfiyrrtp57c/fFVxQKpamu0K2LDBLJlSUOzHlZGhk8dBEIYNR/yysZH55gpqe4eExPQw05YQ8bAoFAhIfU6zswwA/fStt/MQWHw+jpqMjJUnhuCrSgo6UEpoecvJKpkdfsemoGTbIi4qX+VwSBQP5MpFu8SqsaVsQ+fv0px1BPVUGeKpA20egfKwA1FfrrL3meKy9F+w400oSGPAQCkT6kWN/ffy/333Gvtr6hp7keAY8VbONA5Y0M1AoKy2esv77Qs6fnQEPBtg+BQCDChkd9Z2YfG9Nt/IsJt17GDJJDNb7EqXy0zNJmp/7+txemaQO15TDSzgRN9t78SDc64/lCXQFPJG++lvptvU2hELsbaXDpaucBJUWajAxxR/zrsqq66S7dhNQLBAKBCAMeZRejPnbfybs9HMf6Dnl7cIQSGsEuvbVs7PryCecPTP4h7szvx7ztZz80djUhPKoT7IgBGflVwHKnkIkGuqoCb7wVRAKui4nW4WvvVeXJzn11hd0dBAKBCAqezWoU3WHD2eAk68nejm/PT8QnLhi/G7vw9nY35cbNQsyqGrOIJzudi3x1jj0X3Gh/UFpV77ftLhqD1tdVEWzLvwKPw3btor3u2DMKETugu4ZoOoVAIBA+4cNtgqT0Cjyz+W6POWMCv9L3nlQPfbJmAO0fTwmhi/eSLghE9QPBjLIZDgIRfOBJNaO+ezcd4bllfgZY8UYGGiFxj44FO6vQySLrFwKBQHiGP7c4ztDn773XTCaEVFlu+rS0O0lAg/o111/mPH+f1dNMT5Ti3oSMDFFNhb7xxPP1PgNE3DUEAoHwAJ+3PdklKTdfMIgyyHdnE7/ONTRqb6so39Qz2dvPvVJVphMIOGH280uUlOivUjOefczvZawslgFAIBAI9/Cl78zMw9PGH9Pe8OSgwgpL79FrbR+F9BSiDf/3rbSS0qpePQ2E10X7oFBILU3ldceenggZLvL1AwQCgXQMPvS9JnXzmDn3rLe/md9NG7V3/yXT0aMC7V9ssqUJRfk4HMT5+5811BVQKJQw2ucSWVlKcVFp0tucfmZqYhwGBAKB/BZe9Z1T/iBo5PI0t5Nvp/yIh0SojNx+ZKqZ8xi/Ia9jnRWRDeV5eRVMBCO/ismpK835/h2DQZOVVOl4nrX/zdfSgqJKKx0Rxcy0gzydevNFJtR3CAQi4fCm76z8C/M9NzFmXNs5UuWf5OkohWGbjs2/NWj8LMfUU+65Ib17b8n+5+jQ/nqhCATZ83ruaQeeEzNeePSFSiVh0OLP1U6kkO68/Bow0QqDFudKAgKBQNqHN31HK484nM9p9SJS1m7rV87Wxufq0VmcaP5G1opn73MVFQSTYYZP8Disgizpyfs8m27QhIdAIJKLdOSfqWey84sqtbT4cc5wmAU3H+5d9TxNzW7dMQtFvtYBSvLU1+mFUN8hEIgkIx36/r2oms3hYHkvpMeqTA45dSCF3kMHk1bP/3gwWEx2YRX/7UAgEIjwkA59/5ZfiecrDzurod6wf3CgblXU3uR3/I+HjUQVlEF9h0AgEo106HteMQOP4ycDMI5uO4WOQDR8Fsx4UGhUYVmNYNqCQCAQ4SAd+l5VW4/BiD9yphk0GlNQyhD3KCAQCKQ9pEPf8Rg0h9M6XkeMYNBIMlHAFUUgEAhEsEiHvqvKk+vqmeIexb9wWCwiu6y8vJxGo4l7LBAIBNI20qHvhmq0+roGcY/iX3AoTuLOhUrb5w4fPnz8+PHOzs5EIlHcg4JAIJD/IB36rq1CYbJYHA6Hx7TAHGZdeVE9G8EsZ3A4DXVleZVoNBJPp5B5zEOJRnIcR826eWYXmUzes2fPzJkzgdCPGzfOwcEBi4V+GwgEIhFIh76jkEgahVBVXStD4clMbvj0KGzCi9J/fnq0ZvgjBALba9fseX14E/jSsupJ02a9uX/22rVrW7ZsOXTo0MmTJ8PDw6dMmTJq1Cgg9P369RNvHjQIBAKRDn0HWHVVS80s51HfcV3tNr20E9BI0ChEyteiwIlWQNA3b97s6+t77Ngx30a+fv164sQJ8KS4uHjs2LFA6C0tLQXULQQCgXQMqdH3MXYG86Jv6+mIv7AGFYvQUpJRppOAfK9ZsyYwMNDLy+vSpUt9+vTR0dFZ1si7d++A6IPXgRU/rhFjY2NxDxwCgfxZSI2+m+spEHHoyqoaHk14wVFeXunQSxvxIwoeHRISEh0dHRcX5+npefXqVVNT06ZjunbturqRp0+fHj9+fPDgwYqKiuPHjwdGvZaWlliHD4FA/hSkRt8Bbv0NEpK/dTHWFOMYFGWw117lLRvXq+nH0aNHR0REIJHIqKgoJyenpKQkDQ2Nlsf3bmT9+vX37t0DFr2FhUWXLl2AOQ9OBIovjk8AgUD+FKRJ372dup6587G8gkGjCr+S9y8oyC/2HGCoQPtnDYFCoUJDQ4ODg589e1ZSUmJvb//w4cOfhRscZtfItm3brl27Biz6wMDAPn36AKF3d3eHQfQQCEQYSJO+k/CYBaMstp5N6WGmy2OgJH+o0TC33heHT7dp+SIQ6PDw8Pj4eF9f3/z8fFdX16tXr/5KsrFYrEsjNTU1Fy5cAEK/cOHCwYMHwyB6CAQicKRJ3wEj++ufufM5O7dYQ01BxF3LEDFPUr75evYk/TeTJZhpwsLCAgIC3NzcgNADK97DwyMxMRGHay/2Ekj52EbKysrOnTsHg+ghEIjAkTJ9B0TN7j9+dQKFTJSlkUXWKQ6Dqiwu0VOlDu2t8/O7wB4Hyn769OkxY8Zs3bp14sSJXl5ep06dQnNRTVBWVnZaI8D2h0H0EAhEgEifvqsrUqJ97RZtu2tkqCGaWBo0ColrYBRW1W7zs/+VWyg0NNTPz8/T0xNo+sGDB52dnefOnbtr1y7u/UjKysodDKJnFn/+jtHTpUlQYk0IBCJBSJ++A3oaKoVO6xsc97iriRaJiBdqXxg0ioaqf/OleO9SRwLul78uR0dHBQWFY8eOAeMdh8NduHDB3t4+ICAgMjKyoz1yG0TPLrgwffibzc83WRJ4+2gQCKRzI5X6DhjYQ3PFBFbkkSe6OqrydBkh9ULGo+sry1/nlscsGET5XULgsLCwmTNnAjnGYDAkEunixYtA4oHoL168mLfefxNEz6ouZqBJuB/rA075gxWeG1S3nVho0tZsx2HWMtEErBjuSEMgEDEirfoOGGalo6Uk47/jHqOaoa6uhEIJWL/UaNhHLzO66SrsXz6UxEV1QDs7OyC7hw4d8vb2Bj8CLU5MTLSxsVFSUpo0aRI/I2k7iH6UbWYVRwWoNqfiQfDkqJuowKbKsuzSZyevcxw9e9PRCE5d1p1dK/1XHqpY8PJtuLlwlzoihc3mfC2ouvs6Jy2rrKi8ppJRV13TUN/A5IBZmYCjkLDyVKIqnWyuL29nro7HQR8W5E9EivUd0FVH/mTo8LADj958+KahoUilCuaOK5WAQTNrrj1MX+DZ08Vaj/sTga09sZGm4BkNDY2bN28OGDCARqO5ubnxOarWQfRHtp78/F5v9nB6f8TGU0rWWkh1WfDXZOWcnu0ZaXTGdQzQ/UcR83ZU9uquQ9HSGGHYKcS9tp51+UnmrZdZnzOLKxo3M5NJeBwOi8Pi6SRSY5EvZEMDs4HJzCquTc+tvPLka0jsQ3UlqlUXVfd+usaacuL+BBCI6JBufQdQiNh1PgNuv/i+7dyr/PxiJSU6jUbhuTUaEd3AYDx4mtani2rc8qFqCh1rCljrxsbGcXFxs2fPbnrF0NAwPj6+aRPTwIEDeR5YS/4Joh+ALb9ZrOxmvSFkXSYbWcGW+XrnfLllzhS/jJlXDvb6MdNRrYMOW9c89etG8ggwk/bQ+oLy2n2J728++dLAZMnTqRrqCjQqiZv4IhaLXVZenfQ+/9LDNGU6eY6buYOlOLdAQyAiQ+r1vYlBFpoDe2rcfZkVm/A2N6dIS53OweDIJG5vPOIxSDKaU1ZeeS8l366nxv5lQzWVePTph4aGjho1aurUqXj8PwazlZXVkSNHRo8eDWx5MzMz3pptg4aK8gaO0Ztj1Y4HXobkuNqfvh23aev0R5Turr7Zdxq6/BNEz3h98ALa84xpW78KZl5CwJSNld4Hto7VlOALoby6fvPZN7eff8GgUZoaih293YJGo8Ap4MHRUSksrog48iTmzMsFnj0cLGEiIEgnR4K/1h0EhUQClQePV2mFt15kPk7N/VjG0FGTk6WSkBgMk40E33M2AonDohFsNhLBwaERGCSivr7+e27Z94JKMz2FvqaqS716KcryZekCNe/Ro8eePXt8fX2bX7S3t9+9e7ejo+P9+/cNDAz4/qw/+HF7ter5potuR16PMigKIihbTje/saI+0mc0KSo8fMY/QfQjkUcu4UbFd/1Z3ms+xU1z9DnxjTRuCU2Cr4Kbr3LWHX3CZHEMdFX53PGARCKVFGjgUVxSuebI09N3P6+bY0sl8VjjBQKRfCT4m80rPQwUwQM8KSyrSX6f+zGzNK+kurKytrSqrri8hlHHpMsQ5GTw8lSiHJWgo0QZ2U+3u77iD90XEGFhYS4uLjNmzGiZb2DkyJGFhYXOzs63b99WV1fnvxeg71VM8rDN28aoo2s/fSvKTgo42mXjs8XTtDGhfv8Pop83N+1dttnEA2+fT2wZRM8uS143fv4bp9CZzwPKZ/Sh8j8aIcBksaNOpSTc/6SmStfSEGQuNmDLy8lSvmTmewRd3DB3QNPVAoF0PjqhvjcDLPHh1nrDrUXdL7DfbWxsduzY0SoyctasWSUlJU5OTsCK5z+nGM540Y23niQTTQyCU1eUXVhROuLovsna//xBm4Lo5/X9YDB9WA81Sssgen3q58UjVpQuurTLdG/vKMfdVsKKLuWH6jqm77b7n78WdjXRpMoIPp0cCoXU11EpKa1cGHN7vkeP0XZGAu8CAhE7nVnfxciqVascHBzmzJlDJv/HpbB8+fLi4mIg8Tdu3CCR+JMtJFHd9J/tTsTu89dFK0wFlnzTz+zq7EyGgjbhyb7ritOubwnsglvzTxC9/UBrRhlDf9Tik/3qM3aeZAyLteT9brSwAOI+f+v9r9klPc31sYJbV/0MXU6GRCLsjH/NZnPG2sMCLJDOBtR3oWBqajpo0KCYmJgVK1a0emvdunVTpkwBBvXp06fbz0HGNUiS0eglLQ3QqqerHRwP1urRizhO8QpNAtm7d++eKu8/HqHUL9+tnXvDqmdvAqNWd97zmkITiiRlomexOcv3JadnFvUw0xWquDdBwGNNjLV2nE9RkScP7K7x+xMgEOkB6ruwCAkJGTBgwLx586jU//i3kUhkXFych4eHt7f34cOHhZLomGq363NZQNL5I4cOHhqtqtJve/KF2XpYREN5OU2z7uTaxX1GTV4ZMCxiXRUl+7mRUahEZaKPOpXy6kO2uakOFiuii5NIwHUx0QrZ/yhmgZ25vgRNdRAIn0B9FxbGxsbDhg2Ljo4ODg5u9RYajT527JiLi8vChQuBjS+U7pEkrX7jA8Bje9mXL2zNxtwKxG6+fz+bvzcTCH/c1lUnChl6LOrMXXc2cz7cPCEZmegffyy6dO9jty5aBIJIw1rIJIKujkrAngdnw90EeKcdAhEvUN+FCDDhraysfH195eRab5skkUjnz5+3tbWNiIgIDAwU4iAwsrqGLX9uFP6FyHu7b5nvje797nY2i/jX2LFeEpCJvp7JXn/8mbIiTSwldulyMuVllXGJqbPdzEXfOwQiDKC+CxE9PT0PD4+NGzeGh4f//C6NRrt586aNjQ2dTvfx8RHlwBpyX2XrT4lwdzX3cm1+UeyZ6I/fTc8rLO/d0/D3hwoHNTXFYzc/uNrodXTfMgQimUB9Fy7ANre0tPTz81NQaKPgVFMOMmAmA4kfO3asyEaFNZh78dYv3+14JnoB0MBiH7mSqquljEaLraQJHo/V0VDccT4lfEY/cY0BAhEgUN+Fi7a2NlDG9evXR0VFtXmAgYHBxYsXBw8eDCYA8K+Ih9c+3GaiFwQ3XuZU19QpKYr5Bq8snXY/Ja2SUS8D97VCpB+o70InICDA3Nz8r7/+AnZxmweYmZnFx8e7ubldunSpT58+Ih4eN/wmE70guPAwQ1GeJpay6S0Bqwd1JdrdV1nDbTqQNxQCkUygvgsddXX1SZMmrV27dvPmzb86xtraOi4uztPT8+rVq6ampqIcXodoOxP9uHGjR49W5COIvoHF/vC1UF9XVYBD5RkKlXzj+Teo75BOANR3UbBixQqg2v7+/u1knhk+fHhUVJSTk1NSUpKGhkRvtGmdif748cDAwPaD6DkczsmTJ391j+HJx8L6eiaNymceAnZNSvCB6MvE0ecnO2vz7MUnkUmvXqcxahtIBNHFDkEgwgDquyhQVlaePn16ZGQkEMR2DpswYUJJSYm9vf3Dhw/5MYdFxj+Z6F1campqLly4cPzXQfRg0vLy8rpy5cqOHTt+Dq5/mVYoI8NvTCSn6uHduMQ6BILPhtBolKIsKT2n3EyvjVviEIgUAfVdRCxZssTExGTp0qXtO6x9fX3z8/NdXV2vXr0qCbtJuQRI9thGfhVED6QfHHbgwIFXr14BQ97Q8D9BkFkFVQQ8f/czOWVfj4d90Z5plrfvO18N/YBMxBeWMfhuBgIRM1DfRYSCgsKcOXPCw8OB9rV/JDgGWPEeHh6JiYkCSlAjOtoMogefBTxvOgDoe+/evYHQu7u7N59VWlmLw/FzKbJr3my8lmI6KNihfNM+vj5AIyQiLr8E6jtE6oH6LjoWL14M7Nbly5fr6f3m3t3WrVsnTpzo5eV16tQpNFoqt8u3DKIHKl9aWtr8Vnl5OVB8f3//NWvWYDA/rsCK6jo8nttiWz/DqUq6G3dfefwJI7mapwIYO4JEwBaW1wiiJQhEnEB9Fx1ycnILFiwIDQ09ePBg+0cCTQfHODs7z507d9euXWKPGuQHHR0dFovV6kUOh7N+/frk5OQTJ06oqKgwmSw8idcboj88M6EZWv6T+iij2F/5HG0TWCy6po4pkKYgEDEC9V2k+Pn5ARP+48ePv90fhMPhLly4YG9vHxAQEBkZKZrhCYO6urpz5861+da9e/d69uwJJJ5IwDYwW88B3MGuebPp2isTuzAnGTBBsPkZ6b+wmGwZrov3QiASC9R3kUKlUoHEAxP+6NGjvz2YRCJdvHgRSLyCgkKrUlBSBJvNvnnzJvi3vLy8+UUGg5GWllbQyLp165Stp9cweUv5wsi9drm6mn1tad9r4CcO6IeNOOWx7e6Y0auXqfJ686Kmtv7Nw1uZFnKC2r0FgYgFqO+ixtfXF5jwqamp3OxjakpQY2Njo6SkNGnSJBEMT+BgMJicnJyvX79++/bt6/8pLi5uehfMYfr6+gMmaT9IzeepebLWnMSZ9f+325mZLzf4pPXe7TnEiMJH8HpdXUNFwXcLCws7Ozvw9xo4cCDvbUEg4gPqu6ihUCjAGF+1atWpU6e4OV5DQwPYvwMGDKDRaG5ubsIensDBYrERERHJyck/v4VGo4Ehv3DhQlk12o3nvIU1IjEUpX8LyDJr8WgkiqwoI0vlJ0tZWVXt6tWR+7ZvOHz48Ny5c8EUBVR+woQJ4kqLD4HwBtR3MTBv3rxNmza9evWqR48e3BwP7P34+PimraHSaEsGBga2OTOxWCwqlTp27FgGE73x2FM2m4NC8XcnGaPTJ/IZnxl8ZAjoovIaXVUqDov28fGZM2fOjRs3tm3bFhAQ4O3tDeQeOm0g0gLUdzEAzMAVK1aEhIQA1ebyFCsrqyNHjowePRrY8mZmZkIdnsAZPny4ubn569evf35r4sSJYEFDQSCU6JSy8iq6nMzPx4gYdn2tTTe15ipOSCRySCPp6ek7duywsLAAU+yCBQukcaKF/GlAfRcPs2bNWr9+/dOnT3v37s3lKfb29rt373Z0dLx//76BgYFQhydA2Gz2hQsXqqur23x39uzZTU/sLTWvPc+SBH3PySub4GDy8+v6+vobN24MCws7dOgQdNpApAKo7+IBj8cHBgYCEz4hIYH7s0aOHFlYWOjs7Hz79u12UpVJCEwm88SJE5GRkSQSafr06eDzcjiclgfY2NgAu77pudcgw2PX34PJQASFotpBiYJ9/qK0n5narw4gk8mtnDbTpk2bN28edNpAJBCo72ID6EJUVFRSUhKQOe7PAoZ/SUmJk5MTsOIlNkFNXV3dgQMH1q1bp6mpuXnz5iFDhoAXKysrN2zY0NDQ0HwY+CzNz5VkSd0NlLJzSzTVxZnVq6y0bKStwW9LbDc7bTIyMrZv3w6dNhDJBOq72MDhcEFBQStXrrx582aHTly+fHlxcTGQeGBCAtO48TV2wYU5Pp8XHVvcRbwJa6qrq3fv3g00vXv37ocPH245da1atWrcuHGurq7fvn1DNO7mHTNmTMtzgyb29gpLUFKk4XHiScwrT0Lde5p/YpUL96fo6em1ctrMnz9/4sSJ0GkDkQSgvouTyZMnR0ZG3rlzx87OrkMnAtN4ypQpXl5ep0+fBvMEp/JR+OLb6gc2ijFheWlpKbBkY2JiBg0adPHixZ9Dg8A4c3Nza2trbW1tweIDfPZWIqihJDOiv8HdN3nGhmJwPeGxqM8ZuXNGmNPI+I6e2+y0AVP11q1bAwMDodMGIglAfRcnwNwLCQkJDg6+d+9eh05EIpFxcXEeHh7e3t6HD+97v23BOfO1z6xlxJKnJj8/Hxjs+/btc3Nze/DggZGRUZuHvXnzBhi2QPotLS2BGjbfWW2Jr0f3m88zi4orFOSpQh51a+SwrHwk0q2fPs8tgD+KQyMtnTa+vr4dnbwhEEEB9V3MjBs3bs2aNdeuXXN0dOzQiWg0+tixYy4uLr7TXT9fwS2+56Ys8huTmZmZ69evP3r06Pjx41+8eNGOuVpYWOjq6gqmgaYCs3v37m3zMAIOs2HugLmbbuJxWP4rfnCPKgV1Izlt75IhKEGkcmt22hw+fBhY8dBpAxEXUN/FDJDpkEY6qu+Ixs3958/G9dAzqjSdftbg/74ZdtWnK3/fo3pO668gvMzCnz59Wrt27YULF2bMmPH+/XslJaV2DmYwGEDcp0+fPmHChN+23E1XPnJW/8B9D02MNckiSfKlIYu98uDDxnkDNZUEGZ1JJpPnzJkDliktnTZz587V1tYWYC8QSDtAfRc/o0ePjoiIuHz5MjDGO3ouNn0nhuCMy7lxaOdOnxmjnp3YvDo85sLHapVZJmP6DaQKwV/z6tWryMjI27dvL1iw4PPnz3Jycu0fz+FwgK4ZGBgEBQVx2UU/M7Wl43qtO/asi4kWidhhb3iH0KZjL9x+Hzm7fzddocTtNDttvnz5sm3bNktLy187bTjgcGGMAfLHAvVd/KBQqNDQ0ODgYGdn546lem9I27PgsE5oUozNt0EDXbcG+GaqjZzv4fAiFrUptL/AxT0pKWnNmjUpKSmLFi3av38/sE+5OSsgICAnJwfYsB36aM59dVEo5Nq/n2pqKCopyvI44nbBoFE0VP3le+nhM/v1NlERRhct0dXV/dlpAxY0/4+AQlTfn+t0fGLi9n5c/VohEC6A+i4RuLu7h4eHNyWZ4fokVu7ZpbtoC4KqwyYNPIXrMuJ7auLJtbZXFwTprkpxVxGkb+b69etghfH9+/dly5adOXMGj+fWpj506NDp06fBxMBDocFhVjpGGnJLdt77Wl2jqamMRgvy9oISFff1a24xk3UwYJgKXXSK2uy0uXXrVkxMTAunjVbVt/d5rH/y79RmPn2PMe+hhof2PIQfoL5LBMC2BZYdMHXd3Ny43MDJKb8fuvhiAebzYb1Za55sddAnJz+67zLEvl7F+9E03X8DJZnVZUyiLIEXcWxKLQBsdgaDsWLFirFjxzaV0+MSIGH+/v4PHz5UVFTkoXeAnhrt75VOG088v/vqq6oqnU6n8ZuADIGQwaMxrLpbSelu/fTnjOiO5rtBHgB/7sGNtHDa2DoRvsmYy4M/HLv4+iLboRfdkz9v6Q1vyEL4Aeq7pODi4gJMeGDtttr180vQig4RFxZ5DDWW+Ue7+xiWmeIUXlVcQqanIkxNOTVfb+2LWr3hTM2USzdDrSgd0bGWqQU6NOs0k5aWNmHChOPHjxsaGnboxFYQcJjASX3c+xfvu/wm5U26joYCVZbKmy2vQMEyKisfPs2y7qa28y8HMHnwMzCB0MJps3f10kvFD0bGyU5GXYo+XiFjaqHxY5XEqUrZE37LfPlCa9l/PzOnOvNDqYKJBgma95B2gfouQYSGhvr5+Xl6enJTUxtJMR01pWWFkJrXm5d/c963fliZ81CHFWN67TqcjHH0W3klza1LB5Kht5laoKMUFhY6OTlFRETY29vzcPrPmOrKb55vl55dFpeYej8lTUOZSqGQMXg8gfAbtw8wz4kYDru+Lq+w4sXLUsfeOgdWDFNX5K1WlLD44bSZ4d4QuzHeK+zYlpn3PtdaKOA1KGUohGLWyRkjohVjH/77F+QwPhya6zr1YPHEG18PDxb1LgGIdAH1XYJwdHRUUFA4duzYxIkTO3ouK+vE8lNd156WZcRuri6uXbw/+cjt5yN7anJv4bWTWqBD1NfXgyXIqFGjvL29eWvhV+iry4bP6FdRXf/kQ17yu9zkdzl1DWxleTIBj8VhMXgcBotBYzCo+nqw/GA1NDAZtQ2ZeeWyFLxVF9Uhjl16GSuTCGLc4dsu9Xnviymm+KsJRb3DL0w4PHbZpZm2btsUP6Tg/R4eGEz/R95rM04tmRr1FsMmaE32te4k4s5BICoZDXmlNUXlNWVVdRg0kk4laClSlGShd4pfoL5LFmCpPnPmTC8vrw55uhGcigcRa9I0dNc6z9SZuOJqZuL5LaHrfEYPvnqVmxxkv00t0IGBcDhA1ul0+po1a3hupH2oZJyDpRZ4gOe5xdXAqC+trC2uqC2prK2srmezWGqyBHkqQU6GIE8jGqjTFGVJQhqJIKnN/liQ/Sn4il3c07+6njkrY/f3+UEhDisKaAr7vfqQf0TajCm9HTE+IGPswVN2IdblvvN6Nn+shtxb20Ojz6XWqttOWrp0Qg9ZcWbg5I7iyrpbr3Iep+Z++l5SWl7dwGQhkUgcDoNBo8GT+gYmmJ45HASRgFWVp/Q0UnK20u6mKy/uUUsfUN8lCzs7Oy0trUOHDnXM+K16eeIJve+oeUHxw00a3fG9wsNLSko8PDwSExM5WRfCwo6/yszOK0N38z24d5p+s1ODy9QC3BMVFZWWlnbr1q2OBXryiqo8GTxE0JGwqc//kF1dSZyTuN1NmXk/OU8GfWLycoz/jazAnsm3b8VsWb/Ubx6H1mPz+WOTaAn9k7sv2a3/z0qk/suBMX0XfHUOWuyr9OV4UD+b1DtP1/aW0N9JTT3r+J30K8kZ3/PKwWJLTpYsL0/T1lLGYjE/3zlns9lgKVZZXfvgbd7Fh+ngsrYwVp7hYmqqA4WeW6C+SxyrV6+e2EgHYgplBu54/rjVa1u3bgWNgKXAqVOnIuKGvd42xnE1c3x3pSZd4D61APeA1nbs2PH06dPmmG4Il2DUXcO2G/fw7kdFsjLfpWZ9fH7D48jzFRYUFGJwf81PMR9f2wUPNChb4mx1RL4+o2eYi0qTjV7/adv4xV9n37gfavUj+dBwk/yuXodSQ3pbSZpro7KGuTvh3dXHGXV1DWqqdIvuer/NEopCoQgEHHgoNiYjqqmtzy6umLPxppYy1W90z97GyiIZuHQD9V3isLGxMTY2jouLazMDF/eg0eiDBw86OzvP9Zk+Ue3TiFiNDQ8OeRsROpRagHuSk5P9/f2vXr2qrAy/eB0GRTUfM7ep1ElDyXcGycT/7P7xmo3fzobse4lPskqVUjTHLUleZDu+5xwOc69t9wPz588fN0w2YH3Z7At+XdEsDgKDRBBN58VE5KhL1LeazeYcvpV2+MpbJoutpa6gIE/lbW1HJOA01RU01OTzCsr8d9zTVJJZPd1GV6WT3IQQEhJ1JUD+ITQ0dNSoUVOnTuV+J1GbgBXAhbN7LIy7Hao3Ppryt25R6tixP1ILzBxh6TH34NJVLnQBeWozMjLc3d1jY2Olrjas5EHoEfGmdBUSh/1HBLF6My5kur88u2PDBhejyUVs5Sln7+ymfnqwdWvM8r8SyqqJBhO67/maT3bddv3oLKOubhO6inf8/6GwvC4w7nHq5zw9HRUlRQEEpIK5QVVZTkVJNjevdHJE4gLPnqPt+HUqdmKgvksiVlZWPXr02LNnj6+vLy/ns2urmHgKDomoyzg31z5PZaZc6aVAx+6VlZWL/OYtGcAaG/qOhpnkSrxxdblFh+Li26S8vByIe1N+BX7bgvwA3dp1gVXoOTb475GjjHv0PUxPmW1g4Hzh9bmzOzdYddlAHFH0PsHO2d6sduOyc25nvFQk5+bq009FK/cnMZmsnuZ6eLwgI5eAyqup0mVp5J0X3jx+lxfmbU2W2MgosQL1XUIJCwtzcXGZMWNGx5PKMr/uGWp7yv3yMfu7Ux1X5o3Qp6QUlTDz8ko3RgXR3x5xvmW1/cnLEYiT422cxtLvn5ltxE+SRhaL5eHhMXDgQB8fHz6agfwexoudcYxJR59u69WQVYSTRdZ9+lZhGnYubiK99siRIzEbQr7OstpcsdJn4gRJuP9x503eyr33lRRo2pqKQrrZTiLhu3fTTfua5732WuwyRwoRSnxroL5LKMB+t7Gx2bFjx+LFizt4KkZn2r6VF20sNJaiKRpaKkl/Lf6RWiDj7cVefUZhuk+/lbSzx497cZMOXS9xHegwk/4objTvHluwwqBQKNHR0bw2AOEWYs+Ai5dxJmQkBqGpCn5ukNOk1RVXs8ia5NmzZ3ooXzNZpnb18uW1gQHe3t5gutXR0RHXUB9/LFwV+1BNWU5DyNV0USiUgZ7al29587fc2vXXYAIOCtp/gL8OyWXVqlUODg5z5szhMlNjEz9SC5x+EvOFpoova7AcdzchXA37Y8lu1K1P2FSnFYcOr5inFr0rxJiEJJkuOHuxZGRA3DvXIHOebPgNGzY8ePDg4cOH3Gy4hfAJEq/areWGZaze2Jm0fpOXqK6dYl5/K2LZt0lbd29yVPj25QswC3r16jVgwAAw+w4aNEjE48zIrwra84AuRxG2uDejq62SlpGzdOf9aF87/jMUdSY6ub4XlNempBd/za8oKKupqKqrYNSxWRwKCUcl41TkSOqKlO668ppKkrVbvRlTU1Pw5YyJiVmxYgU3x/8ntcCWnYN74ZY7zFmdtHyH1bctiy/3iVzmt/uSmfsBd/fpziTzd7s88AgkzTr01m0eh3fhwoVt27YBfZeREWRZDAjXYHS8jx0pX7Ym0PdUN4/Ft5IGq/8IqNXV1V2/fj0wDo4cOQL0HVi44N+WiYiFSl0D23/HfTweq6st0jAqfV3VT5+z9lx8PWdEd1H2K+F0Qn1n1LFuvMy+8yrr47fi4rIqAh4LrjYsFgMeOCwGiUSUMBgNuRX1DY1b2GvqsGiUkba8XXcNJyttORnhVpPoKCEhIcAKmzdvHpXaXhzYr1ILrHuSwkLjap/t336HbE/4YdcMdpq6f/21CUu8Xy4272towPPAXrx4MX369MuXL2toaPDcCIRfMMqDlhwYtKSNd8Cab/bs2bNmzbp16xaYhoGJAP5eInDaxMS/LSqtsuzB+6XFG0gkUk9P7cTtT0N6aeury4q4d4mlU+n755yKvZffPXrzHSiZnCxFQZFmYKCG+Z3rAEh8WVn1oesftp55bqgpP8/dvE8XoVd74BJjY+Nhw4ZFR0cHBwe3ecBvUgugceDDo8kKhLI336s45o3pxF0H6qoYjJng4nzv9m11dXUeRpWVlTVy5MjY2FgrKyseToeIjJaJiEXgtPleWH3p/id9XRWxOEmwGLS6msLao0/3+A8Rye5pKaCT6PunnIroMykpH3JkZIhdjDRkKB2IOSER8eChpkpnszn5hWVLdt5XppN8R/YY0J0X7RM4wIQHMgq+k60q4XGfWgBnNH3VQMupY1Yf2DLZoOTKmlm7NOc+cWboOTk53b9/n5sENS1hMBguLi7AEgT98viRICKnpdNmwYIF4BXwr8CdNutPviQQcHQ5sfnrlBRlP33MvPr06zArHXGNQaKQen2vZ7Kjz72Jv/tBlkY2N9UhkXh3sACjo2nrRGFRRXDcIyMN2bWz+9NlRFHiuR309PQ8PDw2btwYHh7e9EqHUwugVTwPPKZsX79/yYxyok7vgOvRE/XlUMvLiouBxN+4cYP7LzmLxRo3bpy1tfXy5cv5+VAQsSBUp01OSc2z1KweZnr8N8UzP+Li1RT3J7yF+t6EdOt7VlH1kj1JWbmlXYw0aVTBWCLgElFSpCkqUL99L/RceTFyZv++pqoCaZlnAgMDLS0t/fz8SkpKeEwtgNcc+lfM0L/+89q6deumTJni5eV1+vRpLnPd+Pv7V1VVxcTEdPATQCSIVk6b3r179+/fH5jzfDptTtxJA9YVkdjhQoyCRYZKyvye9zmrzFBDVrwjkQSkWN8fpOaH7H+IxWJ6dtfHYgQcnwe+AzpaSmBNsGz3g7H2Rj4juovRo6etrQ2+jba2tsXFxeB7+Pnz51a+Gt4AnzEuLg4sDry9vQ8fPvzbTSg7d+68du0ab8VUIRKIYJ02D99kK8qLvyQWQE1Z9sazb51P32tqav7++++RI0fKy3ObQVNa9f3Bu4KAPfeUFWW1NHis7ckNQN+7m+nGP/zCqGX6e1kKr6N2AHq6Zs2aFy9elJeXv337FnwnBdg4Go0+duyYi4vLwoUL27fKgbKHhYXx4K+HSDitnDYBAQFNJb9/dtrEx8eDdWSbEVP5ZbXZ+WW9RB420yYEMun6s28+7p0tULK+vn7mzJk+Pj729vajR4/mRuilUt9fZpSs3HtfRVFOU0PoGyjA+sDERPPK029yMvjpLt2E3V1Lrl+/HhER8f3792XLlp05cwb8CyR48+bNgu0FGGvnz58HiwPQV2BgYJvHvHnzZuLEiRcvXjQwkIgvMETg/NZpw+FwVqxYUVVVlZCQ0K1b6y/Cvdc5RAJY1/GqJ5zqgrsbbsYn5JbVo2SMjVxXDnYwxfO6YiYSCZWMhtzi6s5RG6AVTCbzWiPcCL306Xteac3y3fepMiQRiHsTGDTaxFjz6M2PynTScGuh3z5is9kXLlwANjuDwQDfqLFjxzbVcgLPTU1N/f39eQtqbAdgkt+8edPGxoZOp/+cRqawsNDV1RXMK3369BFsvxAJ5Genja+vL5jdwdLt/fv34McBAwacO3du4MCBLc/6nF3GR2gDq/LR8lPHy81nHBpuQKl6uzvh71XPjI700+Y9VkKZTs4qrOyU+t4MN0IvZfrO5nACYh8DW0NfV6Qh6ngc1thIc+Px5910FXSElnL6R2qBEyciIyOBTQ2WyW5ubijUv9kAlZWVp0+fDt4Fi2iBd62oqJiYmOjg4AAkHswoza+DOQaIO+h3woQJAu8UIrE0OW0AYOIH1xtY2DXvsCstLR06dOihQ4fGjBnTfHx+KeO39Tp+CTM95fwT2VFn+/VSB5e7TP+w6f35HT+BgB0z3K68pIDfhiQJsIRq83WgG98bKSgokG59P/Pw24cvBZY99EVT/q0lYPmprq4QdfTpzr8GC7zx/6QW2Lx5yJAhbR62ZMkSExOTpUuXCqTcUisMDAwuXrwIVugKCgrgX0Tj9TRt2jTwelBQkMC7g0gFTU6bO3fuAAux+UVwuY4bNy4nJ8fPz6/plfLKWp6dM5zyV19LFDVkHt/d8PenryUohV6mI/37dFfhJ2SCRMAtiTwwzsGYjzYkjoqKilY3Rbp06TK6kZ89Zk1Ik77X1LNiL73WVFfAYcUzbCVF2fcfvt159d2uh6ag2vxVaoE2Aco7Z86c8PDwPXv2CGoALTEzM4uPjwfrhkuXLvXp0wesIcB3GFhwop9NIRLFuXPnWhmPbDZ70aJFmZmZGzduBJdHdW0DicKjM4RV8ZXByn4X/7TPuLVjlZgFdyISo2exQk7a6vC+9QSPx9RysAIJM5Mcmlfzv5X1ZqRJ32OvfKipre9qLDBt7SjgOtbQUNpy6mV/M3UMmt86Cr9JLfALFi9ebGhouHz5cj09odwJsLa2jouL8/T0nDdv3unTp2E0JKSmpubQoUNtvgXskry8PLD0RDZ+O3jsgNXARuDURq+wNPsRmiXrGVr0YvSrm+/7Tu/Jc0J3LBrFYrXtzZBesFhscHAwN7LejNToO5vNSUhKB8a7eG1JqgypuBB1PyV7kAXv0wz3qQV+BpgkCxYsCA0NPXjwIM8DaJ/hw4dPmTIlKCgIrMoVFYUYfgqRCohEYlEjhYWF4F8g6M3PwZWclZU1d+5csp5nbX0Db+0jSYp4BIlE+b8ZgVFSlEPWFpex+RhzbV2DoqqE5oXlGRKJBL74HTpFavT9aVpxaQXD2Ej82Qrl5KjXn33jTd87nFqgLfz8/IAJ//HjR2NjobgX09LS9u/fD76006dPf/jwIZT4P5yKioo5c+bU1dWBJwwGAzwBS8/a2lpg15eXl3M4nPr6+r7dRpVX8KjvaHoPZdLO3E/5bEOdH4tiZmFRKYfUlc6P/x3ou5Kc+ItYiR2p0ffLj77I0cgt40nEBZlCTnqTXtfAwmM7cAV++vSJx9QCP0GlUoHEg5kczBM8N/IrgF3m5OQUERHh7e0NTHhXV9erV6/CPU1/MuB6y8jISE5O/vktAoEgLy8vKytrqKue9jSTxw4I3XsP0Tt8PihJPdxCD5F/c/XTAm3LuSb8aBOjtl5RtqOFLTshUqPvzz/kKSrwrjLssqQnR6Jfvvxcw0bgFK1MPQJt+2rx9uGxWLSaokzSmxwuTfhXr15FRkbevn1bgKkFfH19gQmfmppqamr6+6O5BhhiY8aMGTVqFBB38GN4eHhJSYmHh0diYiL0wv/JTJs27Wd9B7pfXV2dnZ0dFhZmpCd/+u5nXpvHK7rudGevvrtn5JMaBE7ZxmLB2r58BL9j0KjcoiotJWHFMUsR0qHvdQ3skrJqA301Hs9npj3ZMP8RYvTQFes0qIy8W6sTds/HqZ/up8mjZinKy7zPLPmtvjelFkhJSVm0aNH+/fs7VGavfSgUyuLFi1etWnXq1ClBtQkW2kDW6XQ6GHPzi1u3bp04caKXlxfoCBbh+2MBF8DChQvr6uqaXwFXYEVFBaLxpt+IESNosnL1dQ119Q08RsGjlfQ8tup5CGa0FCyHRsYr06F/Rkr0/UteJQfBwfCaRIxTnV2n4th/xF9dNX8YBdQR89/dmv/1S5mNphJv92o5SHRWYWU7B7RKLYDHC74s1Lx58zZt2gQWB1wG3vyWqKiotLS0W7dutbyDDTT94MGDzs7Oc+fO3bVrFwyU/NPIyck5fPjwgQMHwDXcrO8YDKaqqqrpub29fdOeGlN9xaLiCnVVblNfCY+K8kqHXoLfICKNSIe+fy+s4n13HAKBpA0cOP/f7dTsqm+VTKqCIplnrUKi0IWlbej7r1ILCAMikQi6CAkJiY+P57+1o0eP7tix4+nTpz/nDsThcOBDga9xQEBAZGQk/31BJJ+Ghobz588DWX/8+PGoUaPA6rOmpmbw4MFgggfrPCaT2Xxk8y5WT1uD9Seei13f8VjU6w+Fc93MxDsMCUE69L2gjIHnOXVRK+o+vNi3rbzLX25GvHtLUGhUQVlNy1faTy0gJGbNmrV+/Xogyr179+anneTkZH9//6tXryort10TGXyoixcvAolXUFBYvHgxP31BJJw3b97ExcWB+d7Y2BhcYKdPnwaWBHi9trYWXAbAcGl5cJNzpun5YAuNNYcfMxh1/NTY4R86ASFHIeiqwoiAH0iHvlfV1KMFkeGdVXTjbkzwB+qc0fM8aXy0h8ZiSipqm55zmVpAGIAlc2BgIDDhExISeG4kIyPD3d09NjbWzKw9k6cpQY2NjY2SktKkSZN47g4imZSUlABNB1dyYWHhlClTHj58qK+v3/IAAoHw5cuX2bNnA7u++cVm5wyi8a7mRMeup++ld+uqLcqRtwSLRj55nTl3ZGfLDMwz0qHvZAKWzeZzNxq79uOu81v+Zg1cO3nUAAp/kwUawaEQsR1KLSAkpk2bFhUVlZSUxFvv5eXlQNyDg4OdnZ1/e7CGhsbNmzcHDBhAo9Fg8dXOAZvNBn/TvXv3Xr9+3cXFZe3atUCyf7X0BFP72bNnwSIVmBRNLpqWKcYA3s6m5+6nFZdUytPFU4JVBsVUliMJMH2ItMOjvjOzj43pNv7FhFsvYwbJNV0MnMpHyyxtdurvf3thmja2IedqpO+SrfFvilgIGT37aat3rR1vyHM8qgqdXM/r7rhG2HWftp3adEF2wt9OtjoY/u8Rcti5L85qas4A1jr3qQWEAQ6HCwoKWrlyJfiWdvRcFovl4eExcODAn3MC/wpDQ8P4+HgwJQCJb5UhFiJdpKenH2wErMyAlQAknstdDsnJyaNHj3706FF2dnazc6YJNAoZPKXP8t0P5GTFsFVFhYa7/uDdniWOIu5XkuFR3zHqY/edvNvDcazvkLcHRyihEezSW8vGri+fcP7AZG0sou7t2qFOYQifuPunbBUrn+ycNWGCs0y3t+HmPDrmjNVpdfXM3x/3K6of3952oGHgtv6mhJrSvKbXkHg6hcxjfCQOxcn5+AjYPrdv30b8P8deq/WsyJg8eTIwqe7cuWNnZ9ehE319fSkUSnR0dIfOsrKyOnLkCPiGgxmlfZcORFQwq8uqUTI0Iher0qqqqtOnT8fFxX38+HH8+PGXLl3q0B8RrFbz8/Pv3bvHYDBAIz+XlejbVbVPV9V36blGhgKuUtA+FALm3cfvngONhJe+Wxrh2T+DojtsOBucZD3Z2/Ht+Yn4xAXjd2MX3t7upgyuMVbplzLDMWtCNkzq/sNk1wmOOLLD+eqTojBzdd7mdA1FCjA22WwOCsWL7d2QlZBRyam9Pi/u+r8v4vrsmT2nN29BOUgOZ+7KXX9vmAsMH3V1daB0YWFhGAwGqLx9I6qqoivJDfoF6+Xg4GDwreP+rA0bNjx48ODhw4c8RLWDD7h7925HR8f79+/Dik5ihZl3ddWk6ZE3stkIhcHhF8+s6Ev71VcMWNz79+8/c+bMgAED/vrrL2dnZyy2Y5f/48eP161bB+x3XCOLFi1q87Dw6TbT111P/5KrryuibwEegyrKKwAqMdMVGhz/gQ//O5LSK/DM5rs95owJ/Erfe1I99MmaAbRG+UWruG4869p8ILP40/c6uW56VJ4XbEgkQlGOXFHJkKXxEvSCNQ6fGxfOa+dtUFxa5WSlPzExcdCgQdu3b2/KrgcMIiD0Z8+eXbBggYqKSpPWA5taVlZWgF23ybhx49asWXPt2jWgudwcf+HChW3btgF9l5Hh0U86cuTIwsJCoBFgBSPwelIQLmFmHhw/7pjhvjTGCKVvpzacL65iIVrre3MAO3g+derUt2/fqqnxsk+wpKQEXGZ79uzR1v7N7VMsBrVjkf2kiMSsnCINNaEXWSPg0AhGJYfNCZ5ijYL7M/4Lf/dXcYY+f++9ZjIhpMpy06el3dvaL8aperl5amD64I1nbPm65dKnq9qztCLe9F2wYFDId1+KVntb06mEhISEoUOHKisr9+nTx7iRuXPnstnsly9fAq3ftWvXlClTTExMgNADubexseGtMv1vATZ4SCPc6PuLFy+mT59++fLlNgslc8+sWbPAd97JyQkW3RYTnNKkQy+7rjrqrktEIUy8Qpa3eK+urg7M4i0D2K2trXnvqbHSi6enJ5f31SlEbOxSx2lrr37PYmuoKwpvWxyViKksLimvqt2yYBCYV4TUi/TCZ/wMuyTl5gsGUQb57mzi17mGRq3863VfTy8eMfW48qpbp2fp8b4/6Qde9oZXkzMMRLXiawcqlt1Fmw7EHdFYEOPIkSPgur9z506zpwKFQlk2snTp0vr6erCeBVofGhr66tWrXr16Ndn1VlZWgt36NHr06IiICKDaLi4u7RyWlZUFTO/Y2FgwAP47Xb58eXFxMZD4GzduCGnqgvwLq/zjjaN7Dz3vFr5zqi74OnEaGHUYOQUSCsGpzfuUXqNspCuL/SeAHVyW3bp1AxN5cwA7P2zatKmgoKBDyTDAF+RQ4LCVsUnvP3zT01UjEASfv0hZBvP4ZYaFkVL4DBuCoPbHdC74+qUwMw9PG39Me8OTgworLL1Hr7V9FNKz+UvOLrm3ytV1c/3M4ymRw9X5E3eAobosjYIvr6imUcVswheXVA62/Hf3MxDrqKgoZ2fnNlPp4nA420ZWrVpVVVUFTF2g9fPnz8/IyAAvAq0fNGiQubk5/wYOmFTAFNIU6fir1hgMBlB/Hx8fAUY3rlu3DqxRvLy8gI7AHGTCgVXx+daxfbt3x57/RB88ebZPr39S56Koeob4zDfpT1OXuqx8RTUi1jFqUBgCgjFtypRHjx4J6oY/WAFs2LAB/NvRvy+NjN/iO+jErY+7L77W1lSSlxfYIo+CxxA4dTeT0v8aaznUSkdQzXY++ND3mtTNY+bcs97+Zn43bdTe/ZdMR48KtH+xyfaHD55ddj/Q3umAfsyzI97GRAEtzkYNNDp2+7NZV3HquwoVl/gqf9XUvi1fnDBhwvfv311dXW/dutWOGUuhUJwaAc+B2Xv79m1w/M6dO0tLS4HK8x+E4+7uHh4e3hS/+PO7LBZr3LhxYJEOjG6eu/gZMJcAa9HDw8Pb2/vw4cMwQY3AqXuzqlfPnUpT/Vdc2T6il3JLiSWbefbIXTR5PJVjNpT54u6AodbYF4++r0gJmaYlqFRwTW733bt3/9bt3ibgcvAabNzdQHHD8Wfv3n1RUZGXk5Ph5yIhYlF4Tn1yyhdDdbl9yxw1lcQTaC8t8KrvnPIHQSOXp7mdfDtF+4dtrjJy+5GpZs5j/Ia8jnVWKLu+0DOqamZC5BBSUdb3pjPQFCVVOTw/3/5JjibHb30sKa2ky4nnjwouy6+ZeZOHdaX+FFgJRDMzMxN8E86ePctNRIq8vPyoRsBzMDcAoec/CAd8bUALv8qO4O/vDxYQMTExHWqTG8DnPXbsGFgZLFy4UBjt/8mwG5hYfefBejdMg/xH6/zn29oYwJ70pDqzkKG19q9hc84epNGoBceG2D3MrZ+mJZDc5x11u/+KLtr02GWOzz7mx156k5r6RUdTAUMgEPAdWA2gkEh5EqqmmpH8MstMX3G9z4Au2uJPZCb58KbvrPwL8z03MWZc2zny/1XOUQrDNh2bf2vQ+FmOqQfU/r5YyCnd4mS85d9zqF63so8N4qdkFgaNCphoFRL3SJZG4S1Qkk/UqOgHn6vGO7S9r2fr1q3AjPX19d2xY0eHmtXU1JzSCILvIBwgssCEP336dKuNhWCVcO3aNeEVUwWrlvPnz9va2kZERAQGBgqjiz8QVuZep3ElW+/MG29bsCwx28dHG1Vf8ulL1b2kW0cO/BPAnnBw5pT5ObojZ9J+JNxgMsqw3RwMeK9L/V94cLu3Qy9jZfB4+6Uo/n76/dffkSiUhjKNQiGxUWgkChgJrS0SLApY60gUh1VYXPk5sxiHRQ8wV9+52AHmluEe3vQdrTzicH7rfAFIWbutXzlbG58fKuG0XZCXTwZ2VzfRkvueXaityXv9I95QoODuP0tb7GWJ+0UmnCYzFsjx2rVrefaB8B+EExoa6ufnB2yu5mUEUHZg1ws7ygU0DkYLhken07nfEMsPlTUNj98XvPtanF9WU15VV1VTz6htAIYemYiVlcEr0kiaihRLQ8Uu2gIoqCIyOFWpx2PfWMzyMiYikDh8XdG30gZKjwnWucFXz8ikLpy+NZ+JJBGpvbxWpFy7oYzHghMOvXd0dpj6ZdlwpazLW/bTVz+SE4jtw7PbvX266SqABwLRJyOnPPld7otPBZ++lZZW1rLYHCoJRyHhwF+wvLquoroOfNEUZYl6arIDzdWWjLWArhgekL6bzmtm9PMKvVxAwCspim4ax2NQmZm5Nt3U+pu1F+vdlGexX79+ysrKYGHLT488B+E4OjoqKCiAmWbixImIxnSA4AkYlQg2IjXlIHNwcAASP3bsWGF0weZwkj8UXn2amZJekF9UicWgSSQ8HofFYtE4LIZEwSGRyNr6hszCmvTcynsp2bsvpCARHCMteWAZOFvpyNMEZdoKGA6bjWhak1a/iPGbXJav9zTCikKUJ1VnpX3PuXsfX/zYZ9ILqvv80JhlsxXxGWH27pNOTEicrI5GUiyDbj212b/14PFHHBP/swHDFQQQJsin250b9NRo4DHOwaTpx7oGFlD5sqo6DgchTyWAGfpXhhSEe6RP3+lUwva/Bs+IuobDYUQTDo/HomrLykh4zOKxlr89GGhcQkKCra2tvLy8oMJUOhqEA6z1mTNnenl5lZaWurq6bt68uU+fPgIZyW8BswiYS8CQwBwD/hVgy9W1zBP3Ms7e/VhSVi1Ho8jKUizUFbmpClBTW19WVnX01ued51+Z6Sst9OzeVdJct9XJS/vNRe+4HWlDRZLVddRUnu+fvHzwvQE5z96UPJjT12zCGLfNC2YQZm4e34XU+DdW9FlkcuT2l9rJ6j++AEiC1uC56wfPFdRwBOV27xB4LFqFTgYPkfX4JyB9+o5ojJXc6me/YMttA301YYdLEnFoRE1VFaMuZuEgLp3+QOPOnz8/fPjwS5cuCVxYuQnCsbOz09LS2rdv34EDB6ZPnz5hwgTBjqF9zMzM4uPjgTQI6uPXNbD3X/tw/u4nRm2Dppq8ob5Gh+6+EAk4ogpdVYXOYrFz80pmrb9poCH712gLc32hb63kFnLvgM02fcfN6f34sCddkUokEVXYOx21k/qZm9PIFpffhlu0Wqoyy7Ib9AfoCamAtGDd7hAxIpX6DjDXU1jvY7t0131VVXlVZbqQepElYnKy84E5s2m+XYc2UABdi42NdXd3F2qGlnaCcIDI+vn5gWkgKChISL23g7W1dVxcHDAAr169ymcF8NdfS4P3PyopZ2hrKCgq0PgJrUOjURrqCmqq8nkFpfO33LbroRE0yQqHlQQnAErObu1uLxu3AWNCZNLysr4p9pm7V/V0EMfTvnR7LqPxwmMXXpzmsMUgKsqF/OXatuADplseqQpjv6aQ3O4QsSCt+g7obaJyONBpyc576RnZ2loqPFdnbROgIuo0zI3Hn5376s4Z0R3d8XAdYMBmZ2cDhU1KSvp535PAaRWEs2DBAjabff369W7duokyE04zYPkSFRXV9PF5S4TA5nBir346lPCaLkux7K4vqIgp0I6aCl1ZUfZ5Ws7oVZe3+NqJN+Mgi8UCsyBYaV2//tUY9zHfPGinbuGGgUsnjXZLthh1tIBpVtqYGRul6Lgq+P68pR67Gcp9xoZdCnIQzG3U/yACtztElEixviMa80oeDBi67cyrhOQvWhpKsvxtnWhGgYKpLC2/mVwQPKVvn668Z0Tw8fHJzMz87b4ngZOcnJyRkXHx4sWZM2fu27cPrCFElgmnJRMmTAB6AXpsc2dv+9Qz2ctjkx+/zjTUV1WgC15/gS1vYqSRm186Zc2V4Kl9B1uIoRxzUwZ2oOwqKiozZszYu3cvueryGItFW0wJpR/yWXKD1x2YdMVuW1FWBQshC4wXvK7nugTPdUIbj1jc7hChIt36DsBh0H+NtXTopbXjfMrbtxnqagqyclSebT0lGUxBQemNlDw3G/2jwS5UEr9L1DVr1kyaNIn7fU/8A+YSf39/IKmGhoY9evR49uzZ0kZElgmnJb6+vvn5+WCGAyYq99GZQNyX7H304l12T3M9Ap7v1Ba/RlVZToZCDDvwGINCDhRV0Z9WGdgvX778bwZ2mtfeg7e7O+0rJObVIZC0AZGXjlvmWimKJm8WdLt3PqRe35sw11fctdjhTUZRXEJqypt0XQ15NA5HIBEw3EkqGYfAsJg5heU335SOsjMKmdzn5x2qvAHWE/v373dycuJh3xMPpKWlAav5+PHjQNwRjYE0Li4uwDYkEokiy4TTivDwcGDFe3h4JCYmcuPSZXM4YX+/eP4u29xUR6ji3gSFTDAx1loV93idD7a3iYpQ+3rw4EFsbGx8fPyvM7Cj5IduOhuSvriU8KMeJZJiNnaqaDKaP3r0CLrdOx+dRN+bMNNT2DR/YFZh1Z2X3x+/y32Vkq1MJysryAD7lPNjhxwKi8X8yBDN4bDZLDQSgeSwK6tq0rPLwNq0TxfVUQMM+pmpE/EC/p2ALwww3oGG8rPviRsKCwvBRBIREQGs8qZXgP1uY2MD5pXFixe3PFLYmXBasXXr1okTJ3p5eQHbECxigNxHR0eDuafNg3cnfLj1JN3cVJsohIyDbQIkXk9PbenO+/uXOwpjb2TLDOzTp0+PiopSUvr17jykjNWqW/cFPoh2AX8RsJLgJrc7RLroVPrehIYiZaJjF/Cob2ClpBe+/1ZSWMooraorKq8qraxtYLJlSDi6DEGWgpejEvoYKSwabSHsO2w0Gi0hIQFIraamppCiFevr68eMGTNq1Chvb++WrwNr3cHBYc6cOWRy24GkwsiE0wqg6QcPHgTm6ty5c4ODg4cNG5aamjp27NifQ2veZZb/nfjG2ECdTBLpRiRZGllTU2nZ7vvHgl14uJfeJoLNwC48OBzO1KlTwQhdXV1/fzREquiE+t4MDosGK25hL7q5REND4/Lly0AxgVY229eCAnxFgazT6fQ1a9a0egtoKDDJY2JiVqxY8dt2BJgJpxVgEQPEDsxwYDzl5eWIxsTCQPRbHsNic8KPPJWTo9Dl+ElTxCOKCrS0sspTdz552Rvz2dSbN2+ALXz8+HGwfgLSKZAM7MJj48aNRUVFYJDiHghE8HRmfZc0zMzMwHfey8tL4JWpwZI/LS0NmN5tes9DQkIGDBgwb948KrUDyxSBl6MCE0ZOTk6TuAPAr2Lt2rUtVwYXHmd+zS7u1UM8ZcoBauqKey68HtpbW06Gl9VDSUnJ0aNHgcFeWFgIflFPnz7V0dER9BgFzKNHj4C+Q7d7ZwXqu0gByrh582YXFxeeo8J/BmjKjh07gJr8Sm2BTA8bNiw6Ojo4OJiH9gVSjgr0vnLlyqqqquZXQFNg2KtXr276ERjvsZdfa2koYLFiuyZJRLy6ilzs5bf+Xr24P6tFAPt18JcFkxb4hfycn1kCgW73Tg/Ud1HTVAzE2dlZIAkdgdr6+/sDfVFWVm7nMGDCAwn29fWVk+MrmSLPQTiJiYkMBqPVi2BBsHz58qYbA/dT84tLq40MBDPn8YycvOyFh+nzRvbg5jZ7eno6kPX9+/draWlNmzZt7969UlSHFrrd/wSgvouBpmIg3IcM/gqgqu7u7rGxsb/19ujp6YHuwEo8PDyc5+5awX0QDpCSFy9esNls8JxIJNbU1DS1UFRUBMQRzDrg+bn76QryVLGXfwKrB1VF6sO3OQ6Wv9zx1CqA/cqVK4L1tokG6Hb/E4D6Lh6aioHwU9OuvLwciHtTwVVujg8MDLS0tPTz81NQEHxerfaDcAwMDICUNB0JxB28iMfjq6urwY8xMTHz5s1jc5CpGQVaGkLP4sANNBrl+tNvP+s7mKXAegXIersB7NIBdLv/IUB9Fw/NxUACAgIiIyM7ejqLxQLTw8CBA7mvpKGtrT127Nj169dHRUV1tLsO8XMQzu7du1sewGxESUkJTFFpaWkXL17U7NafUVPPY7Zn1renwe73c1q+pD8g6ngvJR6vbSKZ9ORNRn0Dqzn1WFMAO1B2FAo1c+bM3wSwSzzQ7f7nAPVdbDQVA7GxsdHS0upowSNfX18KhRIdHd2hs8BcYm5uDgzP9p31AqQpCCchIeH169et3iooKACTnJmZ2YYNG8YvNZChEHh0zrCqq2tQ9JH7R/ZX/ueeJhJLoPF+YWMwaFkZfFp2mb4qpWUAO9B3yQxg7xDQ7f5HAfVdnDQVPBo0aJC6ujr3SZ2AID548ODhw4cdTWgDepk0adLatWs3b97c8cHyCDDV79271/IVLBYrJydHpVLJZDKBQCASie8+ZXSo2vJ/4FQzapEkNR0aXWD3NmlkfHDA0rvXL0hFAHuHgG73Pwqo72LGwMAAmLdDhw4FNjU31TCARblt2zag7zIyvJSjXLFihampqb+/P9B6Hk7ngdLSUmAt1tTUMBiMqqqq4uJioC+FhYXAfgfvAok/fvz45XQZPK6Bxw5Y1Yw6dnVyxPGTyQWlLIJ6XzOPJVbmyvzkciMS8RQd4+fPn4OlFR/NSBzQ7f6nAfVd/JiZmR05csTT0/POnTvtFwN58eLF9OnTL1++zHPsPJhFQAuRkZFgkuCthY4C1ijv378HmvLzW/Ly8uCzgFntaMQ1nhWHU89AkckcloHFzJkKuKLv19fe3DyjYeVJfqobEQk4/V6OnUzcodv9DwTqu0Rgb28fFRXl7OzcTqr0rKyskSNHxsbGWllZ8dPXkiVLTExMli5dKjL9WrRo0c/ltnV0dK5evWpkZASe1zcwKbw6QJCyzh4xzRFEhvQpURUfx6VcfWPtY8VzaAseh66q5XU9IZFAt/ufCdR3SaFp39OvioEwGAwXFxcfHx/+ay8oKCjMmTMnPDwcmHJ8NsUl7u7uKioqeXl5za907949MTGxOTkBEYdhsliC6QyrpiKPeFpSzOQgsLwG07NZbLKosleKBuh2/zOB+i5BNO17+rkYCIvFAi9aW1sLKr3w4sWLDQ0NQWt6enoCabAdvnz5sm3btoqKiuZXBg0adP78+ZbJcGSphPyyet7aZ2advHet2GDMbC1KY/hMfVZOIYLQVRnDx06p2roGBVlhFfUVPdDt/scC9V2yaNr31KoYiL+/f1VVVUxMjKB6kZOTW7BgQWhoaKsMjoLlzp07YMz379/39vZ++PChjY1NTU3N2LFjQad4PL7lkap0cmZhNW+9oMnk8ieRl6tpw8cMlUfnfr0c/KJEv49jN372HQF9V5YVXT1FodJUUnXv3r3Q7f4HAvVdsmje99RcDGTnzp3Xrl1LSkoSrPHl5+cHTPiPHz8aG/ObDrcVdXV1R48e3bJlS319/cKFC48cOdLkbpo4cSJ4smnTpp9zb+mqUO+mZPHWHVLOyXlZ1Z2/959dvp6FQJM0B9ksWd5bk6/fVWlFjZJcZ9B3DoczZcqU0aNHDx8+XNxjgYgBqO8SR9O+p379+ikrK6urq4eFhQkkE1krqFQqkHhgwgMtFlSbubm5YDbas2ePhYXFunXrhgwZ0nLL0saNG38V0zmoh/q2sy+AGPG0xQmF1x07NGjsUF6H3QoKHl1SUauvLjWZwtoB/M6Li4t/rgoA+UOA+i6JKCoqJiQkWFtbNzQ0XL16tf2gSZ7x9fUFJnxqaurPdZQ6yrNnz6KjoxMTE8eNG3fv3r2mqJhWtBOwr0InyVII5RUMHlMUCBQks66noRIBJ/VfjaaSqk+ePJHSJDkQ/pH6i7izAgx2DAZTV1cnvC4oFMrixYtXrVp16tQp3lpgMplnz56NiYnJzs6eP3/+tm3beKvuBBjQQ/Nhap4k6HteQbl7f7HVGBEUTW73ffv2dbIofkiHgPouiTAYDFdX17lz53bv3t3d3f3+/ftCMuHnzZu3adOmV69e9ejRo0MnAvnYu3fv9u3b9fT0wCTh5ubW0WQJrRhvb3jh/mcDPd5cNAKDTsa8eFk8oPsAMY6Bf6DbHdIE1HeJA3w5p02bBgQ9KCgIiB0wjZ2cnJKSkn6174kfiETiihUrQkJC4uPjuTzl3bt3wGA/efLkiBEjwFk9e/YUyEg0lWT01GVz80vVVMQZmMiqYQyy0CIRpNuhAd3ukCagvkscAQEBOTk5N2/ebLJkfXx8MjMzf7XviX9mzZq1fv36p0+f9u7du53D2Gz2lStXoqOj3759C4b0/v17gSehXDnJyjvqmqICDYvhaynAM3Ik9N3HmUeDucqnL7FAtzukGajvksWhQ4dOnz7dKhoSGGKTJk36ed+TQMDj8YGBgcCET0hIaPOAyspKMCpgs8vIyCxcuHDs2LFC2iZjpCkHbOfXXwsM9FR/f7SgQaOQuTmFExy7KEpz5Dt0u0NaAvVdggAWur+//88paIAhv3//ficnp1b7ngTFtGnToqKiwKRiY2PT8vWmracHDx60t7cHA+jXr5/Au27FUi/LEQEXyisYNKqoRVaVjExKqx7vYCLifgUIdLtDWgH1XVJIS0ubMGHC8ePHDQ0Nf34XmMzAeLe1tW3e98QHnOqMG3GbNx2vWXBhrxMd+aPxoKCglStX3rx5s+mIlltPX7x4ITJjUIaEi5hps2LPwy7GWiQS/vcnCAh1Gibh/oeYhfY4MbmGBAJ0u0NaAfVdIigsLATmeUREBLCUf3UMjUZLSEgAJrampiaYCXjphlPz7c7B6PUb997j2M5YHBZkJ/f/WJXJkydHRkZev349Kyvr562nosTaVO2vsZabTjzvZqqDx4nCg6xCxVxP+hQ+o18XbSnOOQPd7pCfgfoufoCYjhkzZtSoUcBYbv9IDQ2Ny5cvDx48WFVVtZ2Z4BdUP5zbxT7eYGbAjpRTg/XJ/0kSACaYbt26ubi4ODg4/Lz1VMS42eiVlNf+feODibEWTsj7jDTp+OsPPywcZdGnqxic/oICut0hbQL1XcxwOBwg63Q6nctltZmZ2fHjx728vG7evAmet38wqyrvewlaRUOR8EPMSV1crNS/jV45d4hyC21v3noK2gTq4Ofn5+joyMcHEgxTnbpiMci9l97q6arKyVKE0QWYvlTIyIS77xaM6jmsj44wuhAN0O0O+RVQ38VMVFRUWlrarVu3uLeXgeW+efNmYGsnJSX9qpBTfVbiWt+/1p3/1IBiI7ouvHR70xAFFN12ts3CNQm5o6apc4rTXu46k3Qh/lRB7r9bT0+cOBESEiIJ+g6YMKRLVx355bvvMxg1aqoKgl1PyJIwVaVlj9JLt/nZG2nKCbBl0QPd7pBfAfVdnBw9enTHjh1Pnz7tqJu7qRiIs7Nzm6nHOKU35vWb8G7c/mflriak3ONjei/cOuNlaDc8zXrWoO/+R1+8fTAu+tI3MpVMJ8ha/nXUe5GNbKNFD2zAiIiIy5cvg8lDUJ+RH3oaKp0MHR60L+nzp0wlZXlZQRjyOAySjuc8Sskw01M4HOREwkv3VwC63SHtIN0Xt1STnJzs7+9/9epV3jYKNRUD8fDwSExMbBWQXvVs5wWF0ORwd50ff16NIeO6rrhQ3IBApL/LPFRCfL6s7xc965P3T3raWLBLrs/uOS7Q9v2Ovj8mGBQKFRoaGhwcDGYO8eYJaIZGxscsGHT31fc9F9/k5RWpqshTaRTexkbBY3Ccuidvs1TopBUTrXqbqAh8tCIGmO3Q7Q5pB6jv4iEjI8Pd3T02Nva3PvR2aCoG4u3tffjw4UbJ49R8f/EB393cMuL2JR3tH39bVsmz/YtCvmgM/TBiSMT71Lc+M0dvMphotXyJNf2HxY6i9/N2JoXm1iEQ/ywgwKjCw8Pj4+PBE0F8UAEAPpldT03weJSasz8hNTW1UEOFhsETCEQChotwRjwaiUcyKyqqH70p7KpDXz3dxlxf8JkeRE9TSVXodoe0A9R3MVBeXg7Us8lM5qed5mIgAQEBkZGRCETNq4jxQXYPbniZdG08oLKyLGZT3PmcEvTueWiLeS/SL2kRGy19DpvTeIMRwSr99F1hgMm/WRvBPBEWFgYadHNz+7kQh3ixNlUDjy+55Y9Sc5Pf5b5MyVKVp9BlSRgg82g0DocBA8Zj0XX1DRw2Gzzq65n5xZX5pQxLI2Xrrip/jbZQVxTKrVqxsGHDhpKSEuh2h7QD1HdRw2KxgNE9cOBAHx8f/lsjkfBxS4f28zmgoqW10GeGgr5MYWpePUIxp8XW08TL623M2PO7T4h4HrG7Pw7R8GWnk2P8wAjfrqUPD2/6mxiebPQf946Liwsw4U+fPj1mzBj+RyhwdFVp4DHewaSByX73tfhzVmlpZV1pVW1xeW0Fo57FZsvTiHQZgqwMXkmWBI7sqiOPRkmEr0mAJCUlbdq0KTk5GbrdIe0A9V3U+Pr6UiiU6OhoQTVIyr1QWsAMDA7XUVe31ZPNib4y2iPkUeutp/Vzp9BGXUyr7d+DgNWZunPN98Dtq6+QujqtvfGXu8pPTo7Q0FA/Pz9PT0+Bp7sRIFgMqruBIniIeyCipri4ePz48Xv37oVud0j7dGZ9r61nPftc+CqtKLu4urSitpJRV1PbwEEgwBKeQsLLUwlKskRTHbqtmSpZVPlgwZr6wYMHDx8+5FM3q58EDl1B2hIfYElBy3ftqqGNYjIo4ydNVqVyKore9t0Uerz11lMOEo8jYvGNDhck0XD0mpOj22nf0dFRQUHh2LFjEydO5GecEIHT5HYHSyvodof8lk6o759zKi4kfXn6IT+7oJzNZlOBluOxOCwGi8NRZYkoFJLJYlfXM8vyKj98L0tM/rJqf60SnWJprOxkpd3bWFl4YSMXLlzYtm0b0Pd2KtVxCbnXXyEm/UZO035wdCKCYMgqf8toeFSPUC6qKtGTH2Q3ZfYPbWflnps3+ZTmlNFG1S9Ob9/x1GLfQyPuEz+GhYXNnDnTy8sLg+mEF4n00uR2j4iIEPdAIFJA5/nqsticG69yDl99n55ZRKWS5GTJ3Uy4ylEF5oDyCsarL6W3X2TiMajxjl3H2xuBtb9gh/fixYvp06dfvnz5VzuSOgZKfsjGc6P79TPvfgiV91iunjTvYoLqhvEB5bbfkuPffS+wMVZCoJXtZ3heXbltTYJ8d6egO3tGmdE68KHs7OzA8v/QoUO/zZoAERnQ7Q7pEJ1B3zkIxLXnWXsvvc3JL1NRlutlYQCsde5PR6FQcrKUH5vgtZXLK6r/vvHxYOLbiY5dJg4xEVQ2waysrJEjR8bGxlpZWfHf2r9VTwuxRpUPKUv32R5b8RVvs/xA7D0L94Ns+qoxw8c/ukMikWi95uxKnMNzR6tXr57YiJASvkM6BHS7QzqK1Ot7SWX9qkNPnr3LVlel97Yw5CYguh1oVLJZV3JlVc3JO+nn7qVtmjvAkO/N6wwGw8XFxcfHx83Njc+mfq56Wvd2nb3dsisKlaiPZch+w2NOLn7UPxah210gxUBsbGyMjY3j4uJmz57N58ghfALd7hAekG59f/q5KGT/o7r6hp5mugSCwGxMGQrRtItWQWGZd9Q1H/ce4x2MeW6KxWIBqbW2tuYzafuvqp6Sui89u+d1jzHHkclfa73VqDYRT3IC8IoyYz08BFIMJDQ0dNSoUUBZ8HjRZWOH/Ax0u0N4QIr1/fjdjG2nnikp0kyMNISxmV5JUVZGhrQ/MfVVWkHEjH68eeT9/f2rqqqANPM2Bi6qnqLVRu1JXI/dSWpKIYOlqciC/5r2PfFfDMTKyqpHjx579uwBswU/7UD4AbrdIbwhrfp+9E769tPPDHRVFeSpwuuFSMCZmeq+z8hetP1OjO8gVAe3yezcufPatWutiqlySQeqniJlLP0P7fvvayQS6eLFi/369QPzwbRp0zrae0vCwsJcXFxmzJhBJBL5aQfCG9DtDuEZqdT3qy+yd5x5rqetIlRxbwJouqG++vuPmRFHkldO7sv9iUDZgTK2md+xfQRV9VRRUTEhIcHW1lZeXp4f1z+w321sbHbs2LF48WKeG4HwBnS7Q/hB+vQ9NbMs8tAjDTV5JcWO6SbPIJFIEyPNpNTvO+NTfEZ05+aUN2/eTJw4EVjQBgYG3Hck8KqnoPfz588Dabh06VKfPn14bmfVqlUODg5z5swhk8m/PxoiOKDbHcIPUqbv9Ux2SNxjGpWsriovyn5RKJShgfrJ25/6dVP7bfbBwsJCV1fXzZs3cympdXV1R48eFVLVUzCG2NhYd3d3MG10aLJpiamp6aBBg8Dcs2LFCkENDPJboNsdwidSpu+x1z7lFVb06smjTvEDFovR0lSKOPzkWLBzO454BoMBxH369OnclMDOzc3duXPnnj17LCwshFf11M3NLTs728nJCeiFoiKP2VpCQkIGDBgwb948KlXoPjEIArrdIYJAmvS9tKr+1I13ujrKaLR48tYqyNPSSyvP3k8bNdCwzQM4HM60adOAmRwUFNR+U81VT8eNG3fv3j0jIyMhjPdffHx8MjMzwcRz69Yt3hYHxsbGw4YNA2MODg4W+PAgrWgqqQrd7hA+kSZ93xb/Fpi3Sgoicru3iaqa4p4Lr5376JDaSkkWEBCQk5Nz8+bNX5nh/249zf636qlwR/x/1qxZM2nSJH72PQET3srKytfXV05OuguWSj7r168vKyuDbncIn0iNvtcz2fdeftPSUBDvMEgkvIIc+dbL78Ot9Vq9dejQodOnT/8qGvLnraciTr0Lppz9+/c7OTnxvO8JjNzDw2Pjxo3h4eECHx6kmYcPH27evBm63SH8IzX6fj81v7qmTk4QFZb5hEghX3/6rZW+37p1y9/fH3wzf3Zw/2rrqegBEw8w3m1tbXne9xQYGGhpaenn56egIOaJtrNSXFw8YcIEWFIVIhCkRt8Tk7/Ky1EloeizjAz5ZUpaJaNehvSPnZ6Wlga+k8ePHzc0/Ncvz8XWUzFAo9ESEhJsbGw0NTW5uQPcCm1t7bFjx65fvz4qKkoYw/vDaXK7g9+wi4uLuMcC6QxIjb6/TS9Q5T0mklOfdfHBsf0fPn2rZSLxKlZdXZf1t9bF8jRZoNEoXTW5R6m5jr21EY3RkE5OThEREfb29k0HdGDrqTjQ0NC4fPny4MGDVVVVm8fMPQEBAebm5n/99ZckTFedjCa3O3R/QQSFdOh7dR2zpKzaxEiT1/OTbqwN+Wbk5xTsoECoyLsdfnnvXJTa+YE6PObMoskQ32QUAX2vr68fM2bMqFGjmpKkC2rrqbAxMzMDqw0vL6+bN2+C5x06V11dfdKkSWvXrt28ebOQhvdnAt3uEIEjHfqenlMJrGaewyLZLILm8OAe/UeoUUAL6jLDZ2le9cvNq0bwqu/Ahi8oZYDVNJB1Op2+Zs0agW89FTZgBgJq4uLikpSU1NGSIytWrDA1NfX39wdaL6Th/WlAtztEGEiHvmcXV+FxvBs1KKql2TDLpuecmqzMm4dzMRb99fjYp4NCFRQzoqKiPn36NH369J49ewpj66mwAYLy/ft3Z2fnjibJUVZWBp86MjISLFaEN7w/B+h2hwgJ6dD3gpIaPI7vodYmX1o85xMDgZDrb7sssrsS7w2i0Jhnt8+eTT6Ox+Pj4+OFt/VU2CxfvjwzM9PDwyMxMbFDNwmWLFliYmKydOlSaG/yD3S7Q4SEdOh7XQMTzX+pPLy53cqTvUozvj+MfRTlww7Y00ebx4S3WAw6/dklZTp906ZNI0eO5HdgYmXr1q1A3729vQ8fPsz9FKWgoDBnzhwgSXv27BHq8Do90O0OER7Soe9UMo7JZPHbCpJIUTEEDxWjrsivbo8upvSc35e3uBYkgjNgcpS9Wo6fn190dLSvry9QeRHvVxIUYNhNxUACAgIiIyO5P3Hx4sWGhoZgBaCn13qrF4RLoNsdIlSkQ99V5cn19Q28ns2pSw09FldsFbilq1zjHVokEoVEsPmZMDgsNRXFpUsnAo07d+7cli1b/P39582bN3PmTJHlGxAgTcVAbGxsgMr4+PhweZacnNyCBQtCQ0MPHjwo1OF1VqDbHSJspEPfTTRl6+qZvJ6NxGnYyFUvuxN3kDjGSZFYWfh4y+Mssq57F57Xw3gUQknux31UYPyOauT58+dA5fX19b28vIA5b2Jiwmvb4kFRUTExMXHQoEHq6urcFwMByxdgwn/8+NHYmPcStX8s0O0OETbSoe/KskQWiw0evIVIImkOw5YH3T+2/9LKGLAKwNC7m0zeO9CCzvP9UBaTqSz3nzgZS0vLQ4cO5eXl7dq1C6hkjx49Fi5cOHToUCm66WpgYJCQkADGrKyszGXmeiqVCiQemPBHjx4V9vA6GdDtDhEB0qHvAE0VWnlFNV1OhqezUXhtT4flng4CGkxJefUg8zZy0KuoqKxatWrFihXHjh0LCAhYtGjRggULJk+eLC1lj8zMzI4cOeLp6Xnnzh0ui4GAxQow4VNTU01NTYU9vE4DdLtDRIPU6Hs/M/Vbr7J51XdBgscgn38ptvYZ8MsD8Pipjdy7dy8mJmblypXe3t7z5s3T1tYW5Th5w97ePioqytnZuc1caT9DoVAWL14MZrVTp06JYHidAA6HA6Z86HaHiACB6zun8s3BFYsij9//VFyPlDUaPCkoJnJiFzLfXorx9oanb38A3w2xezxIKFZvExVyW/nfWzGgka9fv27bts3S0nLQoEHA2gWviGCQ/NC074n7YiBg6tq0adOrV6969Ogh/NFJPevXry8vL4e53SEiQMD6zim5Msdu2nXbdYefjDKjlibvnD1u8lBMl4+bevEYad6MCp2sKk8pLq1UoIuzPhyYWzJzSjxsO1AgUEdHZ8OGDU1xJrNmzSKTyU1Jx4CZL7xx8knTvicui4EQicQVK1aEhITEx8eLZnjSC1gVgbnw6dOnGIzULJ0h0gtvFxnz236Xbj7lq9/c8zPCIdiFFyd1Hfli1qNn4T0bSIMC9s6dMq2fAhAFXY2AYLvNbsmfKjm9iPxb3VOGdY05kyJefVelYt6/rxxk0eFMZ0DW586d6+Pj05Q0GAjo7EZUVFSEMU7+adr3xGUxEDBvAbMUyFbv3r1FMDYppamk6v79+zU1ec2UB4F0BN70HaM9OXbnuW6zZ8WNuDGTdnv57NNqwU+CepORCPLAGYsHNh3Eqki/uW3jY5xtZB85gbhUXK31DiS+yy8oU1aSFUR7HQaDRr56/93HvTsey+NWJiQS6dTIhw8ftmzZYmpqOnz4cGDOW1hYCHao/NO874mbYiBgLRIYGAhM+ISEBNEMT+pocrt7eXk5OzuLeyyQPwVeF4kYjXF79pwzm+WzU0Z343H1sCdLu7fwwFTeGKM15FQZAqHhHHX7qI++YCLAkEhE6LS+8zbfkpeXwYhjs6g8nlOIRrn0FcB2TRMTk507d65Zs2bv3r0jR47U0dGRwE2wTfue+vXrp6ysPG3atPYPBgdERUUlJSXZ2NiIZnjSBXS7Q0QP705AtKrnjr1nu3hMuGm18e0iU0LL98jWmx+/XpL97vahiBA7x/qHt4J6CiZA0ExPwba7xpsveYYGos5MqyqLu3b//ZYFdgK8vysnJ7d06VJJ3gSrqKgITHJbW1t5efn29z3hcLigoKCVK1fevHlTZMOTFqDbHSIW+LnamMVpGdXgv6zUr5VsY/kWO49QZHVjM/DobWuJema4Kjxp4ZkhggpsDJpkNS4s4Xt2kaa66EqAyhDQT19lTHLs0kWb5xpSv0TCN8EaGBicP39++PDhly5dan/f0+TJkyMjI+/cuWNnZyeq0UkB0O0OERe863vt240Tg/O8E5N0g+0nL3R/c8hVCcUpuz7demZ+wMMLk9Qb/QxIFAaFYNYzOQIbMIKIx+xd4jBlzdU8DFpFWU5wDf8SChGd9S2vt4nKpKFdhdqRxG6CBbIeGxvr7u5+//79dvY9AeM0JCQkODj43r17ohyeJAPd7hAxwqu+M15FjQ8tmHR5zVBrombw8Z5T57mnHh+lImM2zKhk7MIZ6xXWje9OK085uizsDdV5lSVFoINWlCXt9neYGnkVjUYpKnSgMAUPyJGxWZm5qvKkxWN7CbWjZiRzE6ybm1t2draTk1NSUlI7+57GjRu3Zs2aa9euOTo6inJ4Egt0u0PECG/6Xv08ckJ44YRLa+1/RMaY+h0IOmoxY/YJ6zPj1Ucdurt7qV/kGPMVVcDW1rQZt+PWJnclHgvr/RpNJZl9S4fMj77FYNRqaiihUEKxcJUo6Odvv5jrKSwbbyViG1oCN8H6+PhkZma2v+8JjUaHNAL1HQHd7hBxw9tlR7ZcndqwuvlHonnwG2bwPz/Qes7afXfWbgGM7TfoqtKOh7iEHnic+uGbrp4akcBbLve2wWFQdBzr+qNPC0b1HG4tzvzmErUJFtjmkyZNan/f0+jRo4G5evny5T98/z10u0PEjnSbFTIk3Ia5A87e+xxz5qWWmrwsnYbF8vuJgJ2uTMF8TM/NbmDtWTJER0Wc26makZBNsEgkEgiWk5NTO/ueUCgUGGdwcLCzs7PY7xyIC+h2h0gC0q3vTXgMMLQ2VTt0JTXxSQZQeaoclbdi3MBmlyNw3qflpVfWTnEyBWY7hqd0xMJDEjbB4nA4YLzb2tq2s+/J3d09PDw8Pj4ePBHZwCQK6HaHSAKdQd8RjQWelk2wmuFqduTa+/gH6cryFBkZEhpHIJF+b97iMUgcgsWorvnwuYiIx0weZurYS1tIDn2BIPZNsDQaLSEhwcbGRlNTc8KECW2OMCwsLCAgwM3NDZjzohmV5ADd7hAJoVNdf/JU4sJRFrNczZ99yE9+n/v4XW5pZZ2GEpVCwqHQaDwWg8UBixwJ1s4NDUw2iw3+LalgZOZVdNNT6NNVdbpTV2MtUQRcCgoxboLV0NC4fPny4MGDVVVV7e3tfz7AxcUFmPCnT58eM2aMsAcjUUC3O0Ry6FT63gSwwW27q4MHeF5QyviQWZJXUg2Evqyqrqi8ppbJppCwKjQCXYYgTyVoKlO7aNN5zicjCYhrE6yZmdnx48e9vLxu3rwJnv98QGhoqJ+fn6enp0QlXRAq0O0OkSg6ob63REmOpCT3+wzmnQCxbIIFlvvmzZuBqZ6UlAQs+lbvOjo6KigoHDt2bOLEicIbg0Sxbt066HaHSA6dXN//QES8CbapGAgwV+/fv0+jtd5rFhYWBlYSYKYRvCeayWS8fP3m7sv0rNKS0qriBmQZC12OISAQSFlkgxwWoUAjKqjI6VqYmNtZ4HCiuM4fPHgQHR395MkT6HaHSAjwQuyciHITbFMxEA8Pj8TERBzuP7sQ7OzstLS0wHzj7e0tmM7Ky98diU9K+vCkGvdRTtO0MEO3NFuRUaLNKJerraTUM9AcdilBppRALSbRMkhyVx5lpB97Y4aqsuqi0t/TTldXWTDD+ImioiIw1cXGxkK3O0RygPremRHZJtimYiCg8cOHD7daKKxevXpiI62kv6OwP366HX04rojMQGHtvn31zn7bI+8jgVn/2xOrcKTnql2SP3abn1KkKYOZ5mXTZ0Abdwv4gcPhTJkyZdy4cdDtDpEooL7/EQh7E2xzMRCwVoiMjGz5lo2NjbGxcVxc3OzZs3lrnJ2TeyV0Z1wZVaYOM/vlqf6ZL5GIDiSsA0b9wG/PwWPxoyPX9PpuKqogHH88c/LA/n2NeBvPz6xbt66ioiI8PFxQDUIgAgHq+x+EUDfBNhUDAWqupaXl4+PT8i3Q46hRo8AygoeOCmMPB13KYLGRy57F9cp5x88I0WyWU9rDoelJ97QtYsoqL1zRWLnUXYbEb1oL6HaHSCzwivzjEN4mWEVFxcTERLA4UFdXb1kMxMrKqkePHnv27AGLhg40V1v7YE5AONNg7NcXU1IuojiCSTIN2rH7+tzm++ttVmMn5FVHLHY2M+TdKQ/d7hBJBur7H4qQNsEaGBgkJCQMHTpUWVm5ZTGQsLAwFxeXGTNmEInEdk7/l+Li3dNCL1P0192KNs//zM+Q2gTHavjr0ZHe2e/8mexZY/t6DjHloRHododIOFDf/3QEvgnWzMzsyJEjnp6ed+7caS4GAux3GxubHTt2LF68+PdNFBXtnrrqAU718LkgWm0Vb8PgBtvMFwdOrpjLCkMiER4OHZZ46HaHSDhQ3yE/EOwmWHt7+6ioKGDVPnz4sLkYyKpVqxwcHObMmfObGM36+tPTAq9SjGPjQ4Uq7k2oVhbGnF01Ex2hoEAd0KMDPhbododIPvDShPyLADfBNu17alkMxNTUdNCgQTExMStWrGjnxLvzQg7JdN15aY1cbQXvn6QjaFbkx5xfvQCLlfV3Mtf/ZWmqlkC3O0QqgPoOaQOBbIJt2vfUshhISEjIgAEDwMqASm07q37pmQsRdVpbbqxXrywQzCfhDqPibyuubV9JIpxa64n7XTIi6HaHSAtQ3yG/hP9NsE37npqLgRgbGw8bNiw6Ojo4OLiNoxmMHftuupQWdSn8IsBPwSUDM55c+fb20BWTGa7m7R8J3e4QaQHqO+Q38LMJtnnfU3MxEGDCW1lZAcWXk2udivn9+l0P5Q1P3dorlI/BBQuv7pikbOxsraem8MuC8NDtDpEi4DUK4RbeNsE27Xvq16+fsrLytGnT9PT0gEUfFRUF5ont27eXlpb+s9+1pmbT6+q5b+PJ9TWi+DBtoVJVPDrt3s7zOqtn9GvzAOh2h0gXUN8hHYOHTbCKiooJCQm2trby8vJubm7u7u6urq779u0rLi4GLzYdk/n32Swi3fnzA1F9jrYZf+eIq4FdJaP3z/taodsdInVAfYfwQkc3wRoYGJw/f3748OFDhgw5ceIEm80G4g5e//jxY9MBN669dMgqQHHYovsMbUGpZ/Suy7ubkjXcWq/VW2DNAd3uEOkC6juEdzq0CRZIvKam5rFjx1q+WFBQUFZWJovH32TL+3+5JKqBt8fglBtXnvVspe8PHjwAHxCWVIVIF/BihQgAbjbBgmng1atXP58L5gatvLJiAq17/ifeeq9GIJYhEIcQiEoEQgaBmAxsbbDC4K0tBMI25VbUp0mMOiYJ/8+3o6ioqKmk6s81qiAQSQbqO0RgtLMJdvfu3cD4bfOsz58/M75UdStM4zmDmD8CcRqY2AiEGQLxChjgCAQbgdjB66cgNdRq4Nnp2WVmegqI/5dUnTBhApifeG0SAhEPUN8hAqZ5E+yzZ8+io6P19fXHjRvXTjYbYL9jigiqlUW8dcdCIJIRCAcEoilqvScC0a/xFX5QYVYVljGankdFRVVWVq5evZq/JiEQMQD1HSIsevXqdeTIkdzc3K1btwKV/NVhnz59UiZ1U2CU8dYLmDfGIxBrEYiXCER3BOJNo7gH8Djkf1BuqM4v+aHv0O0OkWrgVQsRLqqqqiYmJmz2LwNjUlNTTSx6GFWX8NyFHwKRgUA039KdhkDM47mtRhTqKwvLa6DbHSLtQH2HCJ3o6Og2XwdGMZPJ/Pz5c7UlmtTA47YmDgKxEoG4gEA8bZT4FATCHYFYhEBs43m4CAQJyc6tbYBud4i0A/UdIlxqampmzZqVn59fWFiYl5dX0Ah4Ul5eDsQdi8WSyWRWTUk5/pcpAdqnqlHK1yEQvRp/7Nko9wv40/dKPOXx1b+h2x0i7UB9hwgXoO9BQUFEIhGHw6FQKBqNRqFQzMzMwI8NDQ3gXzoAhywkt05HwyXAfmc23mVtpqExfoYfvnFQj2+ce/YkCbrdIVINvHwhwgWot7GxcVJSUpvvzpw5c/PmzYmbjqd/5TEhMDD7hyIQkQjEgMb4yPeNz/lMIFBFVz98/jZ0u0OkHajvEKHj6ur6s77Ly8vv2bPHw8MDPFcx0r6XxOPmJhQCcQCBWIJA2DRudCIjEF4IxAb+BpzDxmmp0PlrAwIRP1DfIcKFxWL9nG3RwcHh4MGDampqTT92ceiTmphRj8biWA08dCGLQOxtfAiE0q7d86uYumptVyCBQKQIqO8QoVBVVXX16tWLFy9evnwZ6Duw1psSiuHx+DVr1ixatKhlKSh5eRl9VO0T9W79M1+Kb8j/cGfQaJtuajgMj+XFIRDJAeo7RJBkZWVdunQpPj4+KSnJ2trazc0tLCxMS0tr8eLFmzZtMjU1PXr0qLl5GwWSHCw0bmZYSYK+31AyHWWhJe5RQCACAOo7RAC8ePHiYiPfvn1zcnKaPn36yZMnZWRkmg9wdXWtr69fv349gUBoswX78Y7bX5SteLCfNxeNoCiyHZxaVL/JTE2MY4BABAXUdwiP1NXV3blz58KFC0DWgWqPGDFi48aN/fv3bzPVjF0j7bSmQKf0U8YeNRs29dVFYY2YCw4On+uuq4P/XYltCEQqgPoO6RjFxcWXL18Gmn7jxo1u3boBw/z69evGxsb8tzzfz21Kfp3L5weK1aX8t8YDn1zGXsvnnJxnKpbeIRCBA/UdwhWfPn1qMtVTUlIGDx7s5ua2Y8cORUVFAXahpkwbZaUZkzlh9U1+Np/yCIcis6HPhJkDTGjkXxYahECki86r79XVZQ+Snz5I/ZBTUVDVUMJCl2AIZVhyPRpLZtUpMBmyWIQcGaetLtfdums3O0s0GiXuEUscLBbr0aNHQNPj4+OrqqqAqb58+fJBgwb9yofOP1O8B497k3c7vfegr20nixcep4O2s5F4D1sDEfcLgQiPTqfvlZWp+0/ffpz2pJ78XUbRIvdrt4I0g6piudoKeUY5+BfPrK/AU0pItFKCTCmBmkbX3PAiK/tISk98jXUvvcFjB8vJCEu8pIVWoY3AVP/7778tLCxaRjQKCQIOE+7v4lfPVrxQ0q0gXdjdNXNv4erYIvLeJdYolNA/IwQiMjqPvnMyMx+u3RuXhyvCyzh//vhX9luzgjQ0m/XzkTL1DPXK/+yGB0L/TK3rvU8WO5PyhqpjJs13V1WmiWrgksKvQhtFPAxTXYUQH/ulbNb2c6t0S7NF0OPrGYvXYLpsmDtAU0nm90dDINJDp9D3ysr7K6N3ZmORbOK0lAv2X550tNIbsOuHZDwGjxIi9Vi3YZOyGmx1ZXx8XZXkSEIasuTw29BG0dPfQnuBt91cVOiOMyHClviXvkFL0N0jZ/Trpqsg1I4gENEj9frOSLwWuePGe5LSouS/bb6nIBE81vBsgl5TMe/pySkpl46YO0/8Xu3v1dtxsJmghio5dCi0USwM62eAQKPnYLC+d+OGv78jjC44BOKRwJ1Hyijh3ja9TVSE0QUEIl6kWd85nA8h6wM+onuVFx+5soXArBdUw5R6xpxnp+2/PA1g+D19nbl43lACTpp/Uf9HeKGNwmBYX11DTblAKjHZuO+Ky9GkhloBNl7az26V81/VGPzBgH4qdLIAW4ZAJAeplS0W67b30giO0fJncQ4ZfJZTbhuj4m+HTq1Ylz99ek7ltmB36b3vKoLQRiGhry57YPXITcc0xqp1nfzs7Ijnl/nf3VqtZ3hqWuCxMsqIrlqz3czR8IYqpPMinfrOYt2bsng9wmBvwmqh+meBzbjq5vZ9FQVzQxF7V3tSiFjh9SVYRB/aKCTAyilginXqAKMDF9ViLT3Gf7o16t5x3mz5Mqt+x51nni0n91VT2+ltqqf2x91Ch/xpSKW+v10cuhplsvnqBtHEV8x4eqqYLLt0PWFLgBsWI9Fh8mIMbRQqprry6xcMTs8uO5CoN9zEsQen3Cr9aZ9n13WLv7d/IhuH+2zj+KTXkGSqdmpRnaO+zoFhXdUUeKwFCIFIF9Kn79n7jiwpUg6/s12U8dFL7+wLJtNCdlPXzLMXWafcIyGhjcJGX1129Yx+FdW9n3zIS37X82iP4azaOj1sg0JdpXxtBb2+isKsRWMxpThyMVmulCRbhCF9qmDTKHirLqpjuqr0MlYmEaRmBQaB8I+06XtOTvjltInpT/pkvxVlt0gEJzgxeryq4Y3nBg6WkqKbEhjaKAKoZBz4EzT9FXKLq4FRX1pZW1xRm1dZW1ldz+Zw5GQI8lSCPpWgQCPqq9EUZTt/kCsE0iZSpu83lm2oQCmMe3tV9F1j2cyAS5tCKNR+3dSIeLH93iQ/tFGUqMqTwUPco4BAJBRp0vfap89jWNqhSTtRHLZYBtAz72P37Pf7L7+d59FDxF1LV2gjBAKRBKRJ30/HnDEpYgCRFeMYFiRsHa9sMnawMVj7i6A76Q1thEAgYkd69L2wML6evurVSfGOQrG6dEDV1+tPv41zMBFSF50mtBECgYgXqdH39MNn61CYroUZ4h4IwuHemVijngLX984a2giBQMSF1Oj7jeeZg7985TO9jEDo/fVVUHZJQSlDINnH/pDQRggEInqkRt9vsuRWfuHROVONQGgjEMX/fZGKQGQjEDxsdMGwWf0QJQ/eZHsMMORtPIg/NbQRAoGIEn70nV10eWrX4YcV1n5MWWb0u30jHEbamaDJ3psf6UZnPF+o27F+2d+zsiiKJkVfeRsoMLPfIBDM///IQiBmIRA0BILnO6Tmhemfv3e4RigMbYRAIKKEd31nFyX+NeNvIHJcpM1mfj/mbT/7obGrCeFRHQ99lb75IFNXjWUzf39oWyARCNUWP15EIF42Kj7PsqrwPf1RWQ2XB8PQRggEIhZ+pe/Mb/tduvmUr35zz88Ih2AXXpzUdeSLWY+ehfcmN97uYxddWTwzsefKWZ8jbjeeUH3P22RwXFYrBaY5nf+SMEKOWVVjFvFkp3ORr86x5zyMsiC/TLm6hIcTfwZMSLMRiCgEgp+E38pFWYVljPaPgaGNEAhEvPxK3zHak2N3nus2e1bciBszabeXzz6tFvwk6B9xb1T3GZd7bXk66otTRNMJJKt1Dz8FMVvd/kSRVH4k6SN08V7SBcwBD3gcZX5ZjWJ1h/0hbbIFgZBBIMbz14hiYXZ+aRv6DkMbIRCI5PBr/wxGY9yePefMZvnslNHdeFw97MnS7v/4qxvV/ZJFdMoY9aqo/x+OJChoCa3CGROFxrRVSbWjgCkipvHBp9ySkWxG7b9LFRjaCIFAJJD2/O9oVc8de8928Zhw02rj20Wm/2hio7pf7LE5xUsDw/4gkkEiaDRyJV4AaUauIRANCIQz3+0UKaoryhJhaCMEApFk2r+/yixOy6gG/2Wlfq1kG8ujfqj7Vf8Zl3pGvxqvCU5tURGvXf87v6NU0lLOJ9P5bISDQBxGIHojEHwPB5Gvppf9Ir5nz+kwtBECgUgs7el77duNE4PzvBOTdIPtJy90f3PIVQlV+WjzkdwS1nR90gxwBIfVwGQjlneh7pt7M7kd/zu/KPbsWkB+z2cjtQhECgIxuTGchk+KtA1tLeyTLu6BoY0QCERi+bW+M15FjQ8tmHR5zVBrombw8Z5T57mnHh+lPOTot8ya/6dvrP8cM2TIuTE3ry3oriEnh6P/wv/OaSjPy6tgIhj5VUxOXWnO9+8YDJqspErHcym1JDkqGskpJVDlais69vla0IBAFCIQmjyf34Jvavr6WipQ3CEQiCTzK32vfh45IbxwwqW19nJAg039DgQdtZgx+4T1mfHq6v9KZH21LA6Fk1PTVJNrb39TbUpI795b/l9KL7S/XigCQfa8nnvagXunRm8c45GmufNnXkNwGjes8lK1sy2e45Sm6MNIRwgEItH8St/JlqtTG1Y3/0g0D37DDP7pKJxJ4IeGwN92QuwVncWJ5nGE/zDYUvt6hhU/+i4oikzM08sbrLrwE0APgUAgQkdq8s/Yjndcm1RYjSOS67ndOCokbrhNH2CiIeGFtiEQCERq9J1Mwvemsa/pWY/8cEuc4yAQEog6s3tpi3MMEAgEwgVSo++A8d6OqwprXD7fx7EaxDWGO7MCGpBom25q4hoABAKBcIk06XtPM62uGrRD3V1mvDgvlgHUK6tuJpiu9OoF96VCIBDJR5r0HbBwicekwgbnzw/VKgtF3/shv41d5RR7GSuLvmsIBALpKFKm7yrylMlDu66sWLjr7Cqe0wXzxrsZi04UYA/PshBlpxAIBMIzUqbvgAmj+r76lB9W7hN2fZvIyvV9d3D9i9Zv5aQ+KnQBpMGBQCAQESB9+o5CISOXufrVNmyoYyy5FyuCHgsHDlnY29vH2WxAdw0RdAeBQCACQfr0HYDDotcFus9axdmERi28ux8tiNTBvyLHdfQCswlutgYj+usLrxcIBAIROFKp7wAKEbsrxD1wC9lHxWD1hXXK1cW/P6ejoFA3/CLWIwxnDukyys5I8O1DIBCIMJFWfQdQSbgty50PJ2hNpqoE3dhum/5EgI3XG3fZOCPyaRkyemb/Ltr8piaGQCAQ0SPF+g5AIZFTXMwsuqgGyZBOlWRNvbLHIofvNMLKaudmhRyopvdXVD4835JMaC9zGgQCgUgs0q3vTZjpKZyO9EhM/hKuoClfXjjl3t82Hx6iOB0OrSnrZX12+KwTFZSe6soxTt2MtfgvBAKBQCBiozPoOwCLQbn10x9uo3fjWWaslvaqnNLeDYV90p/1eXZdtTy/nRNZVNrbAS7JXfolk9QzSusG6WjtcuyiqyqIoiQQCAQiVjqJvjeBQiIde2uDR2FZTfL73OR3vXZ1H4FisVSwLFlWrRyigc6qwaEQlRhiKQpfgiWVsDG5VUxNJZk+XVXmdFXtrq+Iw8KSHRAIpJPQqfS9GUVZ4nBrPfDgcBD5pdVA7ssq60qraovKaxqYbFUSrgsFL0clyFOJagpk6GGHQCCdks6p780gkQgVOhluOoVAIH8gnVzfIRAI5I/lf05cGDYm8YCTAAAAAElFTkSuQmCC" alt="" name="图像3" width="380" height="234" align="left" />
import numpy as np # 定义两个sigmoid函数及其倒数
def tanh(x):
return np.tanh(x) def tanh_derivative(x):
return 1.0 - np.tanh(x)*np.tanh(x) def logistic(x):
return 1/(1 + np.exp(-x)) def logistic_derivative(x):
return logistic(x)*(1-logistic(x)) # 定义一个简单神经网络类
class NeuralNetwork:
def __init__(self,layers,activation = 'tanh'):
'''
layers:定义神经网络各层神经元的个数,例如[10,10,3]表示3层神经网络,第一层10个神经元,以此类推
activation:定义神经网络的激活函数,可选值(tanh,logistic)
'''
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_derivative # 定义并初始化权重,怎么初始化?
self.weights = []
for i in range(1,len(layers) - 1):
self.weights.append((2*np.random.random((layers[i-1] + 1,layers[i] + 1))-1)*0.25)
self.weights.append((2*np.random.random((layers[i] + 1,layers[i+1]))-1)*0.25) # 训练
def fit(self,X,y,learning_rate = 0.2,epochs = 10000):
X = np.atleast_2d(X)
temp = np.ones([X.shape[0],X.shape[1] + 1])
temp[:,0:-1] = X
X = temp
y = np.array(y) # 使用抽样梯度算法
for k in range(epochs):
# 从所有样本中,随机取一行
i = np.random.randint(X.shape[0])
a = [X[i]] # 完成正向的所有更新
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l],self.weights[l]))) # 计算输出层错误率
error = y[i] - a[-1]
deltas = [error*self.activation_deriv(a[-1])] # 计算隐藏层
for l in range(len(a) -2,0,-1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse() # 反向更新权重
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta) # 预测,即正向更新过程
def predict(self,x):
x = np.array(x)
temp = np.ones(x.shape[0] + 1)
temp[0:-1] = x
a= temp for l in range(0,len(self.weights)):
a = self.activation(np.dot(a,self.weights[l]))
return a
五、利用神经网络进行异或运算预测
from SimplyNeuralNetwork import NeuralNetwork
import numpy as np nn = NeuralNetwork([2,2,1],'tanh') # 验证异或逻辑
x = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,1,1,0])
nn.fit(x,y)
for i in [0,0],[0,1],[1,0],[1,1]:
print(i,nn.predict(i))
如下倒数4行为预测结果,根据异或运算,和实际结果一致:
六、利用神经网络进行0-9数字预测
import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix,classification_report
from sklearn.preprocessing import LabelBinarizer
from SimplyNeuralNetwork import NeuralNetwork
from sklearn.cross_validation import train_test_split digits = load_digits()
X = digits.data
y = digits.target # 将测试样本值转换为0-1之间的值
X -=X.min()
X /= X.max() nn = NeuralNetwork([64,100,10],'logistic')
X_train,X_test,y_train,y_test = train_test_split(X,y)
labels_train = LabelBinarizer().fit_transform(y_train)
print(y_train)
print(labels_train)
labels_test = LabelBinarizer().fit_transform(y_test)
print("start fitting") nn.fit(X_train,labels_train,epochs = 3000)
predictions = [] for i in range(X_test.shape[0]):
o = nn.predict(X_test[i])
predictions.append(np.argmax(o)) print(confusion_matrix(y_test,predictions))
print(classification_report(y_test, predictions))
如下对角线表示预测成功的记录数,最下方表示预测成功率统计数据,数据显示,成功率93%,预测效果已经很好:
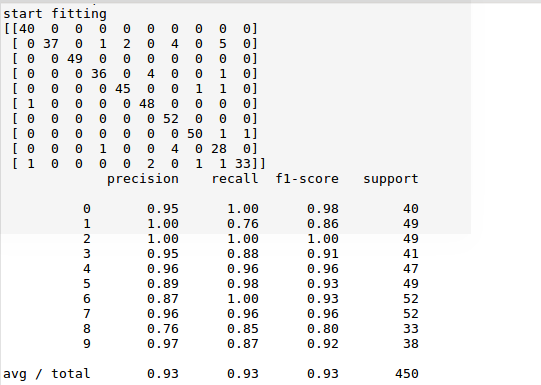
day-11 python自带库实现2层简单神经网络算法的更多相关文章
- day-9 sklearn库和python自带库实现最近邻KNN算法
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一.该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的 ...
- day-8 python自带库实现ID3决策树算法
前一天,我们基于sklearn科学库实现了ID3的决策树程序,本文将基于python自带库实现ID3决策树算法. 一.代码涉及基本知识 1. 为了绘图方便,引入了一个第三方treePlotter模块进 ...
- python自带库及第三方库api察看
今天发现一个很有意思的功能,python自带了所有库的文档查看器,配置如下: 配置pydoc服务,cmd中输入如下代码: python –m pydoc –p 1234 回车后 ,使用过程中,该窗口不 ...
- 升级python的sqlite库版本
今天了解了一下用python获取chrome cookie信息,在研究的过程中,发现打开数据库失败,后来调查了一下发现是由于sqlite3库太老的缘故,起码需要3.8以上,然后看了一下python 2 ...
- python自带的web服务器
python自带的web服务器 python自带的包可以建立简单的web服务器 BaseHTTPServer 提供基本的web服务和处理类 SimpleHTTPServer 包含执行get请求的Sim ...
- 关于python 自带csv库的使用心得 附带操作实例以及excel下乱码的解决
因为上次帮我们产品处理过一个文件,他想生成能excel处理操作的.但是上次由于时间非常紧张,所以并没有处理好. 正好无聊就来好好研究一下 ,找算法要了几个 csv文件.来好好玩一玩. 全篇使用了pyt ...
- python面试题库——3数据库和缓存
第三部分 数据库和缓存(46题) 列举常见的关系型数据库和非关系型都有那些? 关系型数据库: Oracle.DB2.Microsoft SQL Server.Microsoft Access.MySQ ...
- Python 的 Numpy 库
Numpy: # NumPy库介绍 # NumPy的安装 # NumPy系统是Python的一种开源的数值计算扩展 # 可用来存储和处理大型矩阵. # 因为不是Python的内嵌模块,因此 ...
- 【转】使用Python的Requests库进行web接口测试
原文地址:使用Python的Requests库进行web接口测试 1.Requests简介 Requests 是使用 Apache2 Licensed 许可证的 HTTP 库.用 Python 编写, ...
随机推荐
- 导航栏的ul中的li设置问题
在css中 设置li的float:left 可以实现列表在同一行显示 设置每个li的宽度相等,可以实现每个列表的分离状态. 设置每个li中的文字,text-align:center; 可实现每个列表的 ...
- Java面向对象知道这些就够了
面向对象 面向对象是一种思维方式,相对于面向过程而言的. 面向过程在流程中关注动作执行的每一个细节 — 自己动手做 面向对象重点找这个对象,只要找到了对象,那么这个对象所具有的功能就能够被使用 — 找 ...
- CentOS 7 安装oracle 11G
一.安装Oracle前准备 首先要设置主机名,并在/etc/hosts下解析. 镜像没挂全,导致缺少包pdksh-5.2.14.compat-libstdc++-33-3.2.3 1.创建运行orac ...
- 分布式id生成
2016年08月09日 14:15:21 yuanyuanispeak 阅读数:318 编辑 一.需求缘起 几乎所有的业务系统,都有生成一个记录标识的需求,例如: (1)消息标识:message-id ...
- rest_framework--序列化组件
#####序列化组件##### 一.什么是序列化 在python中一切皆对象,把对象从内存中变成可存储或传输的过程称之为序列化. 你写一个django项目肯定是有前后端交互的吧,虽然django也可以 ...
- jquery mobile 移动web(4)
下拉菜单: 设置label 元素的for 属性为 select label 元素的文本内容作为选项的名称 定义div元素并设置data-role 属性值为 fieldcontain. <div ...
- <逆向学习第三天>手动脱FSG壳,修复IAT。
其实对于简单的壳来说,脱壳常用的方法也无非是那几种,但是每种有每种的好处,具体使用那种方法视情况而定,我今天学习的这个壳很简单,但是重点在于修复IAT. 一.查壳: FSG 2.0的壳. 二.脱壳: ...
- Redis学习推荐
Redis快速入门 https://www.yiibai.com/redis/redis_quick_guide.html Redis用途和使用场景 https://blog.csdn.net/wei ...
- Linux Shell常用命令(长期更新)
#判断某个字段是否匹配指定值 awk -F"," '{if($4=="value"){print $1} else {print $0}}' file.txt ...
- jquery 节点
$("ul li:eq(3)") // 元素的index位置工0开始计数,所以这里的3实际为第4个元素 $("ul").find("li" ...
