2 3 5 7的倍数 (51Nod - 1284)[容斥定理]

20180604

给出一个数N，求1至N中，有多少个数不是2 3 5 7的倍数。

例如N = 10，只有1不是2 3 5 7的倍数。

Input

输入1个数N(1 <= N <= 10^18)。

Output

输出不是2 3 5 7的倍数的数共有多少。

Sample Input

10

Sample Output

1

思路：

⒈如果对数学不是很了解，这道题可以按照常规思路来，只是分得不完，毕竟数据太大会爆掉。（20道测试过了7道）

 #include<cstdio>
 #include<cstdlib>
 #include<iostream>
 using namespace std;
 long long n;
 int main()
 {
     scanf("%lld",&n);
     int x=n;
     for(int i=;i<=n;i++)
     {
         if(i%==||i%==||i%==||i%==) x--;
     }
     cout<<x<<endl;
     return ;
 }

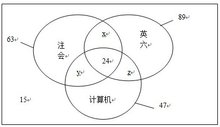
⒉从网上看到了的容斥定理：容斥原理指把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。（摘自百度百科）

如果被计数的事物有A、B两类，那么，A类B类元素个数总和= 属于A类元素个数+ 属于B类元素个数—既是A类又是B类的元素个数。（A∪B = A+B - A∩B)

⒊因为1<=N<=10^18,而long long int的范围刚好包括N。

（https://blog.csdn.net/acm_hmj/article/details/51246118）代码来自于此。

 看了一眼，貌似是2,3,5,7中奇数个数（例：2*3*5）占的范围加，偶数个数（例：2*3）占的范围减去。 

 #include<cstdio>
 #include<cstdlib>
 #include<iostream>
 using namespace std;
 long long n,num,a,b,c,d,ab,ac,ad,bc,bd,cd,abc,abd,bcd,acd,abcd;  

 int main()
 {
     cin>>n;  

     num=;  

     a=n/;
     b=n/;
     c=n/;
     d=n/;  

     ab=n/;
     ac=n/;
     ad=n/;
     bc=n/;
     bd=n/;
     cd=n/;  

     abc=n/;
     abd=n/;
     acd=n/;
     bcd=n/;  

     abcd=n/;  

     num=a+b+c+d-ab-ac-ad-bc-bd-cd+abc+abd+acd+bcd-abcd;  

     cout<<n-num<<endl;
     return ;
 }