SVM中的间隔最大化

参考链接：

1.https://blog.csdn.net/TaiJi1985/article/details/75087742

2.李航《统计学习方法》7.1节 线性可分支持向量机与硬间隔最大化

3.https://zhuanlan.zhihu.com/p/45444502，第三部分 手推SVM

本文目标：理解SVM的原始目标，即间隔最大化，并将其表示为约束最优化问题的转换道理。

背景知识：假设已经知道了分离平面的参数w和b，函数间隔γ'，几何间隔γ，不懂的可以参考书本及其它。

为了将线性可分的数据集彻底分开，并分得最好，SVM的原始目标是找到一个平面（用w,b表示，二维数据中是一条直线，如下图所示），使得该平面与正负两类样本的最近样本点的距离最大化。简单的说，就是任给一个平面w,b，总有一个样本点离它的距离最近（点到平面的距离，可以用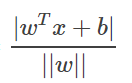来表示），过该样本点作平行于分割平面的平面，两个平面形成分隔带。我们的目标是比较各种平面（无数个），找出一个平面使得“分隔带最胖”。那么如何来表述“分隔带最胖”呢？

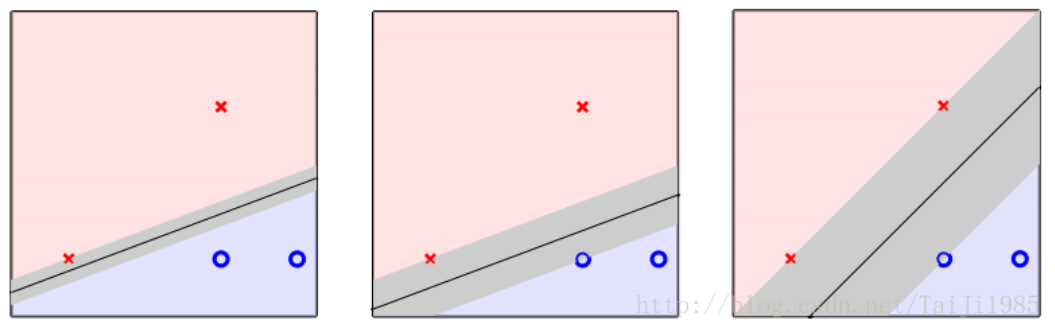(引自参考链接1)

对于平面w,b来说，假设距离平面最近的点是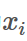，又由于该平面w,b可以将所有样本点正确分类，即满足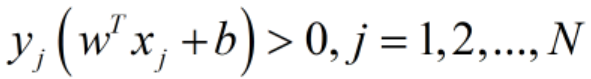，因此我们可以将上述最近点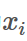到平面w,b的距离改写为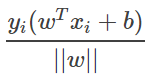，其中取值为+1或-1。因此我们的目标就是最大化，注意该式子中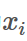已经是离超平面w,b最近点了，称为γ超平面w,b关于训练数据集T的几何间隔。

因此我们的原始问题：求得一个几何间隔最大的分离超平面，可以表示为下述约束最优化问题：

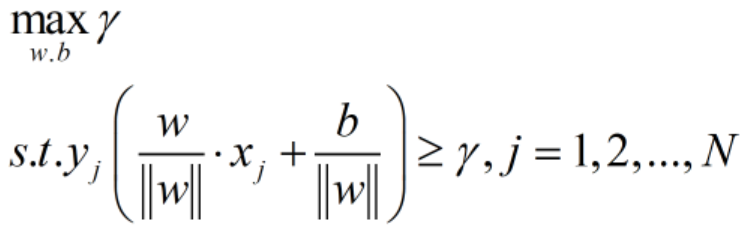
重要问题一：为何会出现第二行中的约束条件？

有了这N个约束条件，好像w,b的可选范围小了很多，跟一开始单纯的最大化几何间隔的任意选w,b有所背离啊？等等，这儿需要注意的是，一开始我们目标是最大化几何间隔，这个几何间隔其实是所有样本点的几何间隔中最小值，而所有样本点的几何间隔有可能是正数（被正确划分），也有可能是负数（被错分）。但是我们一开始讨论最大化几何间隔的时候已经默认平面w,b把训练集T中的所有样本点都正确分类了，只有这样我们才会要求“分隔带最胖”啊，如果有错分的，那分隔带越胖就越不好了。因此满足将所有样本点都正确分类的w,b本来就没多少（限制在一定的范围内了，虽然还是有无数种可能），所以原本我们就要求w,b满足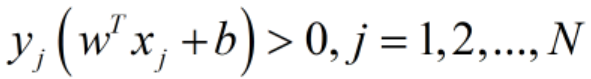，而且还得要求如下，

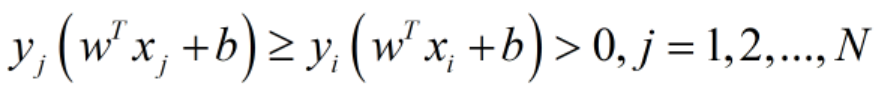，以保证之前是离超平面w,b最近点的设定。

重要问题二：能否对约束最优化问题进行简化？因为目前来看被优化的目标函数γ跟w,b和都有关系，有点不简洁。

解决思路是，对于任意的平面w,b，其实都有无数组参数（λw,λb）λ不为0，都表示该平面。因此我每次选到一个w,b，就相应的知道了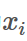最近点（最近点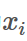其实是依赖于w,b的，称为支持向量，个人理解也可以称作支持样本点），我都缩放一下w,b，使得函数间隔γ'=1，即：

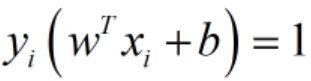。注意到，缩放w,b前后，其所代表的平面是同一个超平面；而且缩放w,b对于目标函数γ毫无影响，因为其分子分母都是缩放相同的倍数；再者，约束条件的不等号两边都是同时缩放相同的倍数，也无影响。因此，如果我们采用枚举法来求解上述最优化问题（为直观理解，其实是枚举不完的），每次我们随机考察一个平面(w,b)，我们都缩放为(w',b')=(λw,λb)，使得函数间隔γ'=1，那么我们依旧在考察同一个平面，依旧能算出和缩放前一样的目标函数γ值，依旧符合同样的约束条件。这么处理（特定缩放）有何好处呢？通过这样的处理，我们把约束最优化问题可以转化为如下形式：

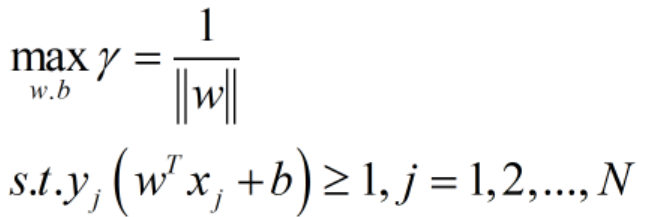
如此形式，简洁明了多了。再者我们可以将max变为min，最大化与最小化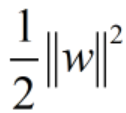是等价的，就得到了如下线性可分支持向量机学习的最优化问题：

PS:

为加深上述重要问题二的理解，我们可以举一个例子来验证它。

假设有A,B两种w,b的方案，A平面的支持向量（最近点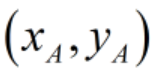），B平面的支持向量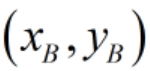，我们来比较A,B方案的优劣。

　    1）首先在原始目标函数下，得到两个平面的γ如下：

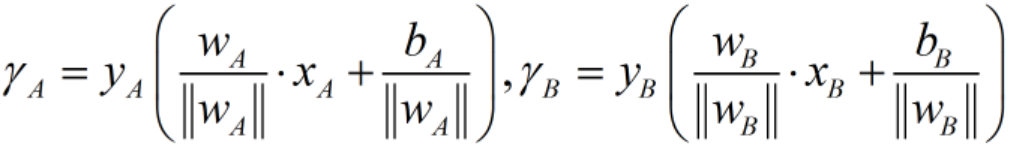
　　我们假设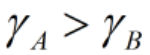，那么我们换种思路来比较A方案与B方案，看看结果是否一致。

　　 2）令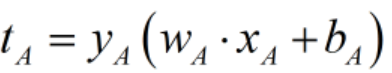，注意到在给定平面A的情况下这是一个数（其实就是平面A关于训练集T的函数间隔）。

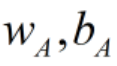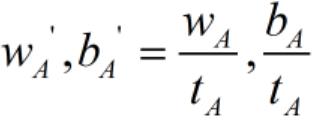　    我们令缩放为，则；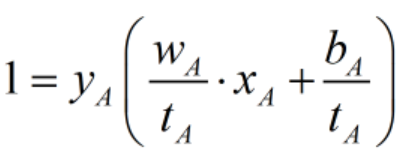

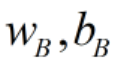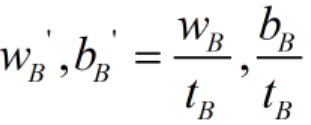　　 同理，对于平面B，我们可以将缩放为，则。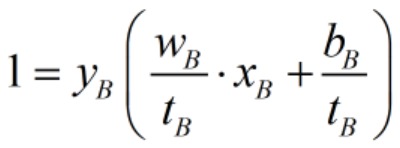

　    现在我们通过比较来确定哪个方案更好，是A还是B？

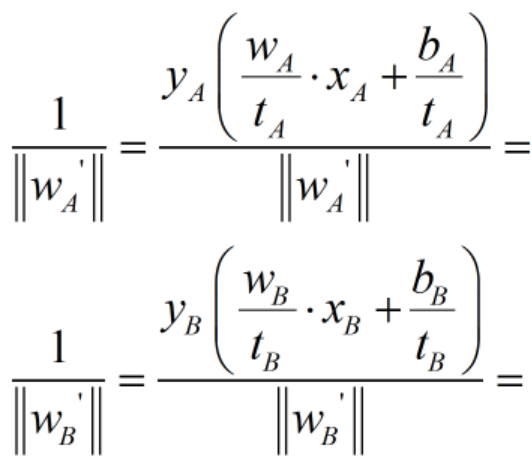
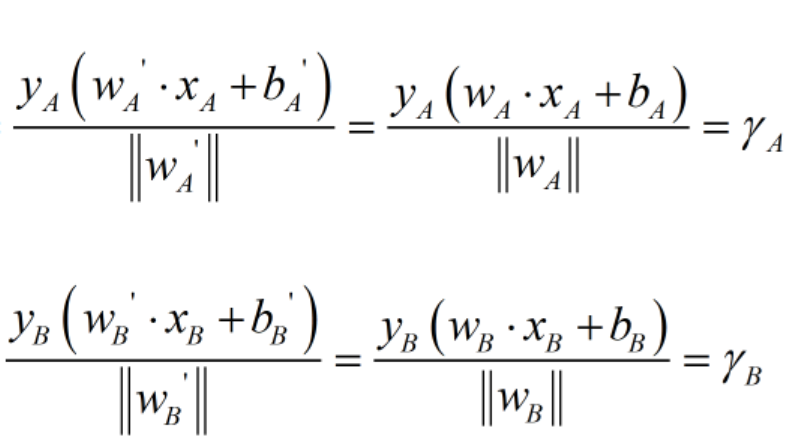
所以我们发现结果是一致的，A优于B，而且目标函数值也与原目标函数值一致。至此，我们验证了准确性，直观感受了w,b缩放前后目标函数值的不变性。