ISLR系列：(4.2)模型选择 Ridge Regression & the Lasso

Linear Model Selection and Regularization

此博文是 An Introduction to Statistical Learning with Applications in R 的系列读书笔记，作为本人的一份学习总结，也希望和朋友们进行交流学习。

该书是The Elements of Statistical Learning 的R语言简明版，包含了对算法的简明介绍以及其R实现，最让我感兴趣的是算法的R语言实现。

【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

Ljt   勿忘初心  无畏未来

作为一个初学者，水平有限，欢迎交流指正。

---

当自变量的维度较高时，一方面可能使得样本量偏少（p>n),另一方面自变量之间很可能会出现多重共线性现象。多重共线性会导致最小二乘的

回归系数不稳定，方差较大（这是因为系数矩阵与其转置矩阵的乘积矩阵不可逆）。收缩法/正则化(shrinkage/regularization)主要是建立包含全体

变量的模型的同时加上对估计系数的限制，即使系数的估计向0收缩。

岭回归从矩阵求解的角度看就是修复病态矩阵X'X，多重共线性导致|X'X|趋于0，那么就给X'X加上一个正常数矩阵 kI (k>0),则X'X+kI接近奇异

的程度就会比X'X接近奇异的程度小得多，从而使回归系数的估计稍有偏差，但是估计的稳定性却可能明显提高；从最小二乘的角度看就是加上一个对

回归系数的二范数惩罚项的有偏最小二乘。

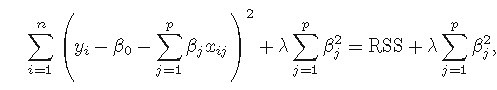
岭回归的一个缺点是在建模时对于引入的全体自变量，罚约束项可以收缩这些变量的待估系数接近0,但并非恰好是0（除非lambda为无穷大）,这

对于模型精度影响不大，但给模型的解释造成了困难。(岭回归虽然减少了模型的复杂度，并没有真正解决变量选择的问题)

Lasso回归是引入回归系数的一范数惩罚项的有偏最小二乘回归，Lasso回归能够使得一些变量的系数为零，从而可以实现变量变量选择的问题。

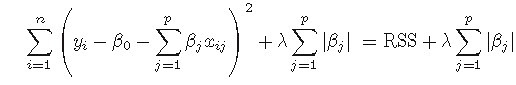
Lasso回归虽然和岭回归的差别在于一个是二范数的约束另一个是一范数的约束，一范数约束能够使得一些变量的回归系数变为0，但是由于其不

连续，求解上便比二范数的要困难的多，Lasso全称为The Least Absolute Shrinkage and Selection Operator，中文翻译为 ‘套索’ ，是目前很多大

牛研究的热门领域。

下图可以解释Lasso回归可以使得一些变量的回归系数为0，而岭回归只能使回归系数趋于0的原因。

---

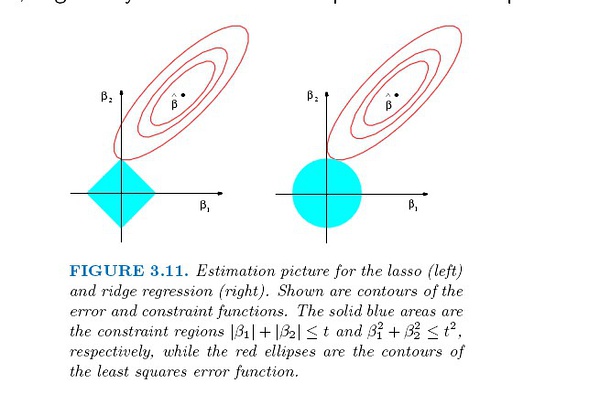
Ridge Regression and the Lasso

glmnet(x, y, family=c("gaussian","binomial","poisson","multinomial"),alpha = 1,nlambda = 100,lambda=NULL)

X：自变量矩阵

Y：因变量

family=c("gaussian","binomial","poisson","multinomial") ：

当Y为数值型时，family为 "gaussian" 或 "binomial"

当Y为两水平的因子类型时，family为 "binomial"

当Y为多水平的因子类型时，family为 "multinomial"

alpha：  0<α<1 : (1-α)/2||β||_2^2+α||β||_1.  ;   alpha=0为岭回归，alpha=1为 Lasso回归

nlambda : lambda的个数，默认为100个

lambda：惩罚系数 λ ，可以人工提供，默认为系统提供

cv.glmnet(x, y, lambda, nfolds）：Does k-fold cross-validation for glmnet

predict(object, newx, s = NULL, type=c("link","response","coefficients","nonzero","class"))

object :glmnet类

newx ：用于预测的新的X矩阵，该参数不能用于type="coefficients"的情况

s ：用于预测的 lambda

type：link，response 返回结果为因变量的预测结果；coefficients 返回结果为模型系数，此时不需要参数newx

> library(ISLR)
> library(glmnet)
> Hitters<-na.omit(Hitters)
>
> #运用交叉验证的方法选择最优的岭回归
> set.seed()
> x<-model.matrix(Salary~.,Hitters)[,-]
> y<-Hitters$Salary
>
> #交叉验证的岭回归
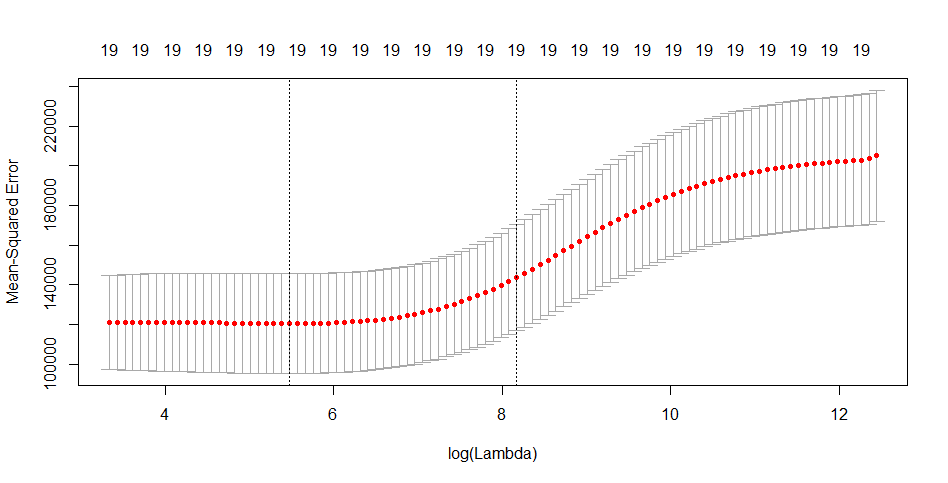
> cv.out<-cv.glmnet(x,y,alpha=)
> plot(cv.out)
>
> names(cv.out)
 [] "lambda"     "cvm"        "cvsd"       "cvup"       "cvlo"       "nzero"      "name"       "glmnet.fit" "lambda.min" "lambda.1se"
>
> bestlam<-cv.out$lambda.min
> bestlam
[] 238.0769
>
> predict(cv.out,type='coefficients',s=bestlam)
 x  sparse Matrix of class "dgCMatrix"

(Intercept)  10.35569016
AtBat         0.04633830
Hits          0.96376522
HmRun         0.27163149
Runs          1.10118079
RBI           0.87606196
Walks         1.75331031
Years         0.50454900
CAtBat        0.01124891
CHits         0.06274116
CHmRun        0.43896753
CRuns         0.12471202
CRBI          0.13253839
CWalks        0.03672947
LeagueN      25.75710229
DivisionW   -88.36043520
PutOuts       0.18483877
Assists       0.03847012
Errors       -1.68470904
NewLeagueN    7.91725602
>
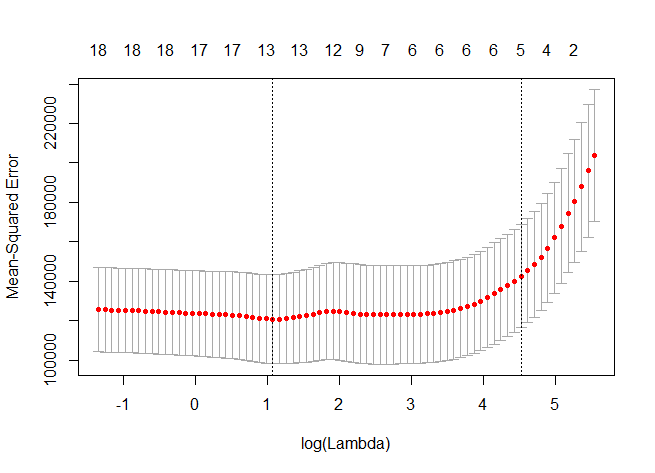
> #交叉验证的Lasso回归
> cv.outlas<-cv.glmnet(x,y,alpha=)
> plot(cv.outlas)
> bestlam<-cv.outlas$lambda.min
> bestlam
[] 2.935124
> predict(cv.outlas,type='coefficients',s=bestlam)
 x  sparse Matrix of class "dgCMatrix"

(Intercept)  117.5258439
AtBat         -1.4742901
Hits           5.4994256
HmRun          .
Runs           .
RBI            .
Walks          4.5991651
Years         -9.1918308
CAtBat         .
CHits          .
CHmRun         0.4806743
CRuns          0.6354799
CRBI           0.3956153
CWalks        -0.4993240
LeagueN       31.6238174
DivisionW   -119.2516409
PutOuts        0.2704287
Assists        0.1594997
Errors        -1.9426357
NewLeagueN     .
>