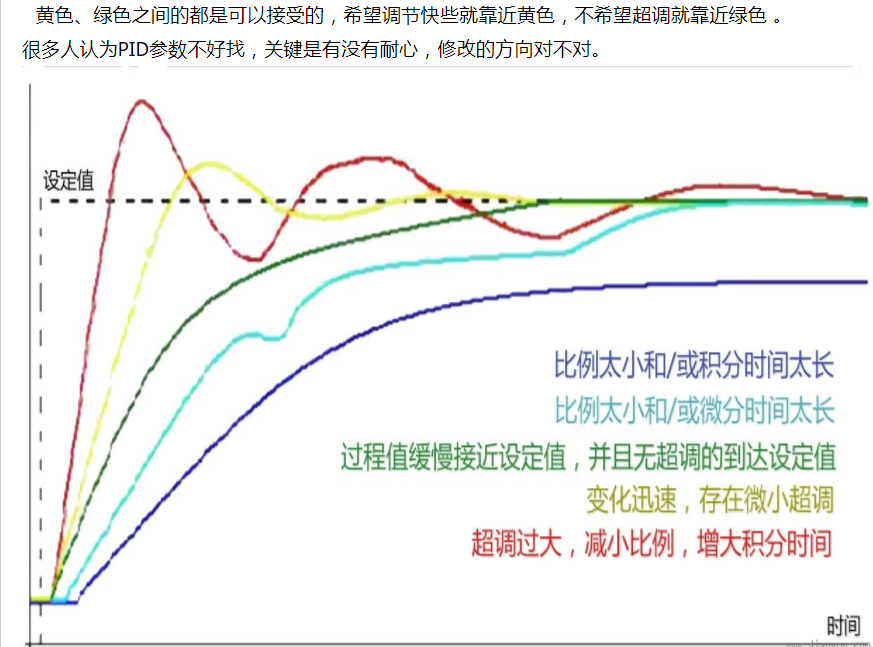
漫谈PID——实现与调参

闲话：

作为一个控制专业的学生，说起PID，真是让我又爱又恨。甚至有时候会觉得我可能这辈子都学不会pid了，但是经过一段时间的反复琢磨，pid也不是很复杂。所以在看懂pid的基础上，写下这篇文章，方便学习和交流。

=======================================================

PID控制器是工业过程控制中广泛采用的一种控制器，其中，P、I、D分别为比例（Proportion）、积分（Integral）、微分（Differential）的简写；将偏差的比例、积分和微分通过线性组合构成控制量，用该控制量对受控对象进行控制，称为PID算法 。

其中KP、KI、KD分别为比例系数、积分系数、微分系数。

比例系数KP ：反应系统当前最基本的误差，系数大，可以加快调节，减小误差，但是过大的比例使系统稳定性下降，甚至造成系统的不稳定。

积分系数KI  ：反应系统的累计误差，使系统消除稳态误差，提高无差度，只要有误差，积分调节就会起作用。

微分系数KD ：反应系统误差的变化率，具有预见性，们可以预见偏差的变化趋势，产生超前的控制效果。因此可以改善系统的动态性能。但是微分对噪声有放大作用，会减弱系统的抗干扰性。

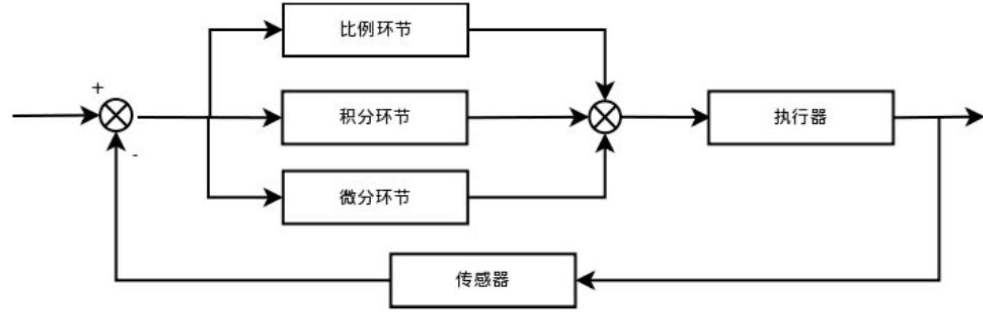转化为数学语言就是：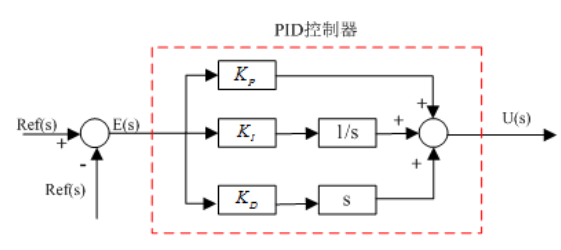

由上面的方框图，可以知道其传递函数（拉式域表达式）为：

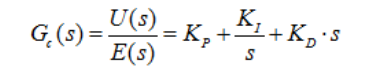
控制理论和数学分析中，我们一般借助拉普拉斯变化和傅里叶变换来帮助我们分析系统的某些特性，比如暂态响应、稳态响应等。但是在程序中，我们只能根据时域中的离散化的表达式来编写算法。

所以将上式转化为时域表达式为：

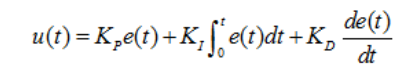
我们需要在计算机中通过编程实现这个式子，而上式又是连续时间的表达式，所以只能先将其离散化，推导出他的差分方程如下：

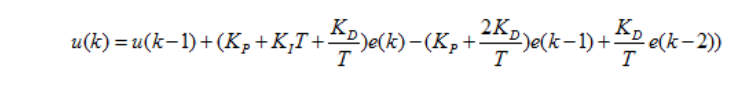......................................（1）

这就是增量式pid算法的差分方程。

其中 T 为PID的计算周期，就是 dt  。其值由微控制器的定时器决定，自己设置pid的运算周期。

e(k) 为本次计算时，传感器反馈的值和设定值之间的差。

e(k-1) 为上次计算时，传感器反馈的值和设定值之间的差。

e(k-2) 为上上次计算时，传感器反馈的值和设定值之间的差。

有了pid算法的差分方程，就可以通过编程来实现这个算法。之所以得通过差分方程来实现，是因为差分方程的一般解法是迭代法，而迭代法只需要知道初值和通项公式就能计算出所有时刻的的值。这是计算机最擅长的事情了。

这个式子就是最本质的离散化PID表达式。后面我将基于他推导出其他几个常见的表达式，但是实质都是这个式子。

在推导其他的表达式之前，请注意这几个变量的 关系：

比例系数：KP

积分系数：KI  =  KP*T/Ti　　其中Ti 为积分时间

微分系数：KD = KP*Td/T    其中Td为微分时间

之所以叫时间，是因为考虑了系统的量纲。

因为pid输出的控制信号应该和被控量或参考信号有同样的物理单位。因为在物理系统中他们是描述的同一种物理量。假设被控量是位移，单位是m, 时间单位是s，那么KI  KD的单位应该为单位1，而根据上面的式子，有一个运算周期T，所以Ti  Td  相应的应该也有与之倒数的时间单位，来抵消T 的单位。所以称之为时间。

因为KP  和 T 都是常数，所以积分系数和积分时间、微分系数和微分时间都是成严格的比例关系的。他们的区别就是数值不一样，实质都是积分项和微分项的系数。如果调节的时候，看到别人说增大积分时间，而你的程序中只有积分系数。那么这时，就应该减小积分系数。其他类推。

对于上面的（1）式，因为  KD/T 是一个常数，KI * T也是常数，所以就有些人由于默认pid运算周期，就把 KD / T直接写成 KD，KI * T直接写成 KI。

其实严格来说，这样写是不严谨的。因为调节过程中，运算周期 T 也是一个很重要的参数。也需要对他进行反复的调节。

在调节完毕之后，我们可以根据这几个常数自己计算他们的乘积，直接写在代码中，以减少以后处理器的运算量。

所以能推导出这么几个式子：

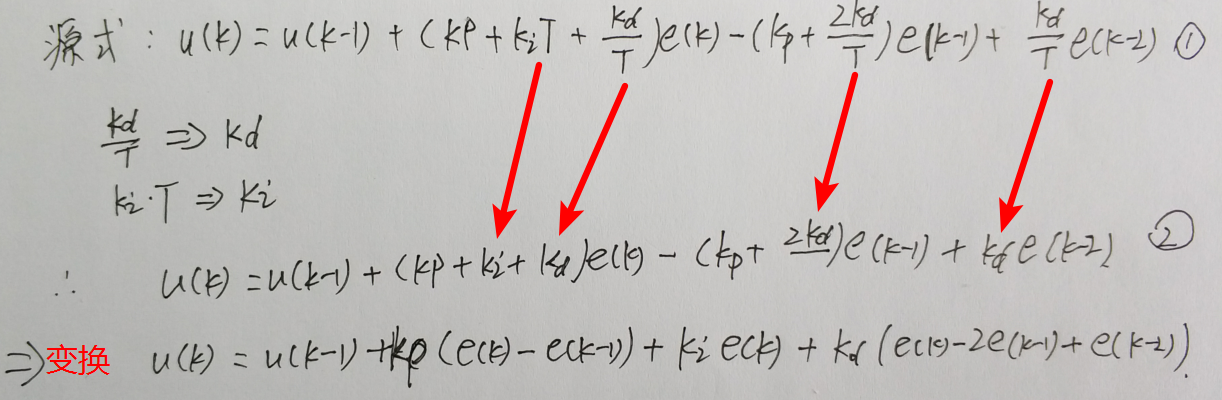
但是不管怎么变换，他的本质都是那个原式，在他的基础上把常量统一了一下，或者做了一下变量代换。增量式pid的式子就一个，同样的迭代式，同样的项，不同的人在不同的程序中取不同的名字，而初学者又容易吧相同名字的变量当成一个东西，以为所有编写代码的人都像商量好一样遵守同样的原则，但是现实中你看到的代码往往事与愿违。不规范的程序到处都是。容易让人产生误解。

==============================================================================

现在根据最初的原式来进行pid算法的实现。

首先做一下变量代换，方便后面进行调试：

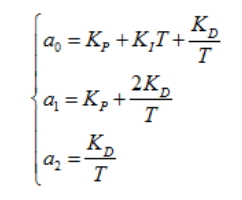
所以差分方程就变成了

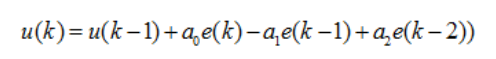
KP不能为0，没有ID或者单个I 、 D的控制器

当KD为0的时候，系统为PI控制器。

当KI为0的时候，系统为PD控制器。

当KD  KI 都不为0的时候，系统为PID控制器。

可以根据系统的情况选择使用不同的控制器。我使用的是PID控制器。

首先就是PID中需要用到的参数的声明，建议最好把需要用到的参数全部都声明一下，就算有的变量显得有些多余，这样可以帮助自己理解。减少BUG

声明pid需要参数的结构体：

 //==================
 //PID.H
 //==================

 #ifndef __PID_H
 #define __PID_H

 //PID计算需要的参数
 typedef struct pid
 {
      float ref;     //系统待调节量的设定值
      float fdb;  //系统待调节量的反馈值，就是传感器实际测量的值

      float KP;                 //比例系数
      float KI;                 //积分系数
      float KD;                 //微分系数

      float T;        //离散化系统的采样周期 

      float a0;         //变量代替三项的运算结果
      float a1;
      float a2;

      float error;    //当前偏差e（k）
      float error_1; //前一步的偏差
      float error_2; //前前一步的偏差

      float output;      //pid控制器的输出
      float output_1;      //pid的前一步输出
      float out_max;      //输出上限
      float out_min;      //输出下限

 }PID_value;                     //定义一个PID_value类型，    此时PID_value为一个数据类型标识符，数据类型为结构体

 //条件编译的判别条件，用于调试
 #define PID_DEBUG  1

 //pid函数声明
 void PID_operation(PID_value *p);
 void PID_out(void);

 float constrain_float(float amt, float low, float high);      //浮点数限幅
 //int constrain_int16(int amt, int low, int high);            //整型数限幅

 #endif

 //========================
 //END OF FILE
 //========================

接下来就是按照上面推导的公式进行编程实现：

 //=============
 //PID.C
 //=============

 #include "main.h"

 #define set_distance 10.00  //设定距离
 #define allow_error 1.0    //死区，允许误差带,0.5太小，系统不稳定，一直在调节，2就太大，

 extern float real_distance ;      //实际距离
 extern PID_value  xdata ASR  ;      

 /* ********************************************************
 ** 作者    ：Andrew
 ** 日期       ：2018.3.8
 ** 说明：
     1、PID默认为PI调节器
     2、使用了条件编译进行功能切换，节省计算时间
        在校正PID参数的时候，将宏定义 PID_DEBUG 设为1；
        校正完毕后，置0；
     3、同时在初始化的时候直接为a0,a1,a2赋值
 ******************************************************** */
 void PID_operation(PID_value *p)
 {

     //使用条件编译进行功能切换
     #if (PID_DEBUG)

     float a0,a1,a2;

     //计算中间变量a0,a1,a2;
     a0 = p->KP + p->KI*p->T + p->KD/p->T ;
     a1 = p->KP + *p->KD/p->T ;
     a2 = p->KD/p->T ;
     //计算输出
     p->output = p->output_1 + a0*p->error - a1*p->error_1 + a2*p->error_2 ;

     #else
     //非调试状态下，直接给a赋值计算输出，减小计算量,因为一旦三个系数确定，T已知，即可自己计算出对应的a
     p->output = p->output_1 + p->a0*p->error - p->a1*p->error_1 + p->a2*p->error_2 ;

     #endif

     //输出限幅
     p->output = constrain_float(p->output,p->out_min,p->out_max);

     //为下次计算迭代
     //这里顺序千万不要搞错，不然输出占空比是错误的。
     p->output_1 = p->output;
     p->error_2 = p->error_1;
     p->error_1 = p->error;

 }

 /* ********************************************************
 ** 作者    ：Andrew
 ** 日期       ：2018.3.8
 ** 说明：
     1、首先根据设定与实际的距离差，判断需要前进还是后退
     2、在误差为     allow_error 之内，停车，防止小车一直在抖，毕竟超声波有误差。
 ******************************************************** */
 void PID_out(void)
 {
     float xdata duty;

     ASR.ref = set_distance;        //距离给定
     ASR.fdb = real_distance;    //获取实际距离反馈

     ASR.error = ASR.ref - ASR.fdb;    //偏差

     PID_operation(&ASR);

     duty = ASR.output;

     if(ASR.error > allow_error)        //设定值大于实际值，小车需要后退
     {
         left_go_back;
         right_go_back;
         Left_Forward_Duty = (int)Low_Speed + (int)duty;        //带符号数和无符号数运算会转换为无符号数
         Right_Forward_Duty = Left_Forward_Duty;        //速度一样
     }
     else if((-ASR.error) > allow_error)    //设定值小于实际值，小车前进
     {
         left_go_ahead;
         right_go_ahead;
         Left_Forward_Duty = (int)Low_Speed + (int)duty;
         Right_Forward_Duty = Left_Forward_Duty ;        //速度一样
     }
     else            //在误差范围内，停车
         car_stop();
 }

 //浮点数限幅,constrain ->约束，限制
 //如果输入不是数字，则返回极端值的平均值
 //isnan函数检测输入是否是数字，is not a number
 float constrain_float(float amt, float low, float high)
 {
 //    if (isnan(amt))                  //51里面没有这个库函数，需要自己实现
 //    {
 //        return (low+high)*0.5f;
 //    }
     return ((amt)<(low)?(low):((amt)>(high)?(high):(amt)));
 }

 /*
 //16位整型数限幅
 int constrain_int16(int amt, int low, int high)
 {
     return ((amt)<(low)?(low):((amt)>(high)?(high):(amt)));
 }
 */

 //========================
 //END OF FILE
 //========================

注意在增量式pid算法中需要对输出结果做限幅处理。根据实际情况选择自己需要的幅度。

关于pid结构体的初始化，我在主函数中使用 memset（）函数进行初始化，比较方便。

初始化之后，就是给赋上自己调试的参数。

    //初始化PI调节器参数全为0, 该函数在string.h
    memset(&ASR, , sizeof(PID_value));

    ASR.KP = distance_kp;
    ASR.KI = distance_ki;
    ASR.KD = distance_kd;
    ASR.T = T0;
    ASR.out_max = limit_max;
    ASR.out_min = limit_min;

然后利用定时器定时调用   PID_out()   函数即可。

============================================================

关于参数的整定：

首先是一位师傅给出的建议，记在这里，作为指导；《大体上是这个架构，采集，然后计算，但是有几个要注意得问题，不注意这些，可能永远调不好PID或者调出来得不理想，首先你的传感器响应速度？以及执行单元执行到温度传感器得时间是多少，这个要去测量一下。比如我加热单元开始加热，我需要0.5得控制精度，那么我从开始加热到传感器发现温度变化0.5所需得时间，t，那么就以这个得0.3-0.6去做采集时间，并以这个采集时间得3-5倍去作为PID计算得时间，并把这个时间，和Ki,Kd系数做一个处理。》

首先得有一个实际的项目，才能进行参数的整定。我采用的是简单的小车距离保持。

主控：STC89C52

超声波模块获取实际距离。三次平均滤波后，精度可达1cm。

程序中我设置距离为10cm，死区为（+-1.0cm）

当仅仅采用比例控制时，小车震荡比较严重，基本无法稳定

PID参数的整定方式：
1、理论计算法：采用被控对象的准确模型进行数学建模。
2、工程整定法：不依赖被控对象的数学模型，直接在控制系统中进行现场整定，也就是现场调试。

其实这个调节关键还是多看，多试，如果有能力进行模型建立的话，那将更加精确。但是一般情况下使用试凑法。刚开始我尝试了不大概30组参数，总是不能达到理想的效果。

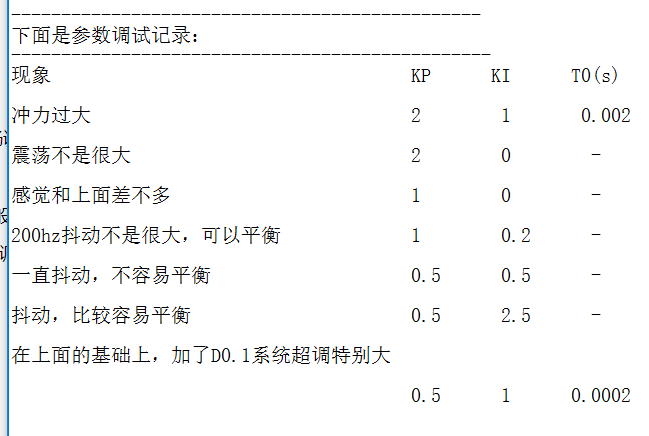
显示比例系数KP一点点的测试，在超调量不大且反应灵敏的基础上增加积分或者微分系数，但是不要一下子全加上。例如我增加了微分，控制小车的震荡，然后对KD进行反复的测试。

最后增加KI用以消除系统的稳态误差，但是注意要一点点的增加。不要加的太多。

进行了pid整定以后，效果如图。但是由于芯片处理速度和电机驱动性的问题，导致一直无法调节到最佳状态。

pid调节大法：

/******************************
参数整定找最佳，从小到大顺序查，
先是比例后积分，最后再把微分加，
曲线振荡很频繁，比例度盘要放大，
曲线漂浮绕大湾，比例度盘往小扳，
曲线偏离回复慢，积分时间往下降，
曲线波动周期长，积分时间再加长，
曲线振荡频率快，先把微分降下来，
动差大来波动慢，微分时间应加长，
理想曲线两个波，前高后低四比一，
一看二调多分析，调节质量不会低
*******************************/

关于PID还有很多很多地方等着去实验，我这里只是面向新手入门的。写的很浅显。但是一点点经验不至于让大家走那么多弯路。能对PID有一个初步的了解，这篇文章的目的算是达到了。

关于项目的完整代码，在我的码云中：https://gitee.com/Andrew_Qian/incremental_pid_car_distance_maintenance

===========================================================

参考资料：

1、原理介绍：http://www.cnblogs.com/cjq0301/p/5184808.html

2、原理介绍：https://wenku.baidu.com/view/827c5423647d27284a735105.html

3、调参经验：http://www.51hei.com/bbs/dpj-51884-1.html

谨以此文祭奠我在pid上面花费的那么多时间。