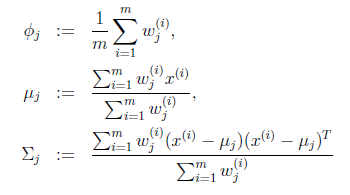高斯混合模型和EM算法
使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是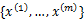 ,我们将隐含类别标签用
,我们将隐含类别标签用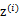 表示。与k-means的硬指定不同,我们首先认为
表示。与k-means的硬指定不同,我们首先认为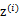 是满足一定的概率分布的,这里我们认为满足多项式分布,
是满足一定的概率分布的,这里我们认为满足多项式分布,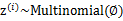 ,其中
,其中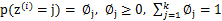 ,
,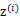 有k个值{1,…,k}可以选取。而且我们认为在给定
有k个值{1,…,k}可以选取。而且我们认为在给定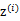 后,
后,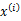 满足多值高斯分布,即
满足多值高斯分布,即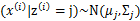 。由此可以得到联合分布
。由此可以得到联合分布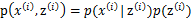 。
。
整个模型简单描述为对于每个样例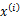 ,我们先从k个类别中按多项式分布抽取一个
,我们先从k个类别中按多项式分布抽取一个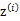 ,然后根据
,然后根据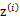 所对应的k个多值高斯分布中的一个生成样例
所对应的k个多值高斯分布中的一个生成样例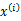 ,。整个过程称作混合高斯模型。注意的是这里的
,。整个过程称作混合高斯模型。注意的是这里的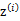 仍然是隐含随机变量。模型中还有三个变量
仍然是隐含随机变量。模型中还有三个变量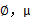 和
和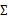 。最大似然估计为
。最大似然估计为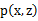 。对数化后如下:
。对数化后如下:
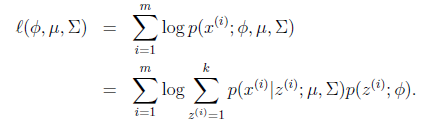
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的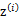 ,那么上式可以简化为:
,那么上式可以简化为:
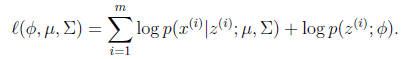
这时候我们再来对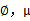 和
和 进行求导得到:
进行求导得到:
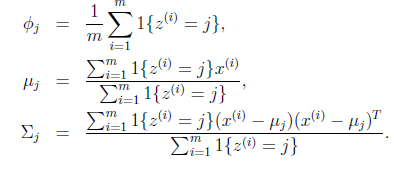
 就是样本类别中
就是样本类别中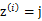 的比率。
的比率。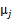 是类别为j的样本特征均值,
是类别为j的样本特征均值,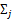 是类别为j的样例的特征的协方差矩阵。
是类别为j的样例的特征的协方差矩阵。
实际上,当知道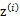 后,最大似然估计就近似于高斯判别分析模型(Gaussian
后,最大似然估计就近似于高斯判别分析模型(Gaussian
discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了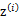 ,实际上
,实际上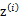 是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
|
循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算
(M步),更新参数:
} |
在E步中,我们将其他参数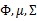 看作常量,计算
看作常量,计算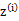 的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,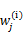 值又不对了,需要重新计算,周而复始,直至收敛。
值又不对了,需要重新计算,周而复始,直至收敛。
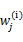 的具体计算公式如下:
的具体计算公式如下:
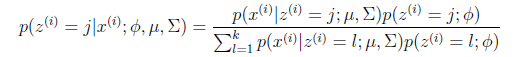
这个式子利用了贝叶斯公式。
这里我们使用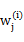 代替了前面的
代替了前面的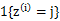 ,由简单的0/1值变成了概率值。
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别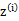 是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
虽然之前再K-means中定性描述了EM的收敛性,仍然没有定量地给出,还有一般化EM的推导过程仍然没有给出。下一篇着重介绍这些内容。
高斯混合模型和EM算法的更多相关文章
- 最大熵模型和EM算法
一.极大似然已经发生的事件是独立重复事件,符合同一分布已经发生的时间是可能性(似然)的事件利用这两个假设,已经发生时间的联合密度值就最大,所以就可以求出总体分布f中参数θ 用极大似然进行机器学习有监督 ...
- 混合高斯模型和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类别标签用表示 ...
- 高斯混合模型参数估计的EM算法
# coding:utf-8 import numpy as np def qq(y,alpha,mu,sigma,K,gama):#计算Q函数 gsum=[] n=len(y) for k in r ...
- 高斯混合聚类及EM实现
一.引言 我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussian Mixture Model (GMM).事实上,GMM 和 k-means 很像,不过 G ...
- 高斯混合模型GMM与EM算法的Python实现
GMM与EM算法的Python实现 高斯混合模型(GMM)是一种常用的聚类模型,通常我们利用最大期望算法(EM)对高斯混合模型中的参数进行估计. 1. 高斯混合模型(Gaussian Mixture ...
- 混合高斯分布与 EM 算法
极大似然估计在混合高斯分布中遇到的困难 在一般的情况下,对于所得到的样本集,\(X=\left\{x_{1}, \dots, x_{N}\right\}\),我们的目标是最大化似然函数,通过最大化似然 ...
- 混合高斯模型和EM
<统计学习方法>这本书上写的太抽象,可参考这位大神的:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html
- HMM模型和Viterbi算法
https://www.cnblogs.com/Denise-hzf/p/6612212.html 一.隐含马尔可夫模型(Hidden Markov Model) 1.简介 隐含马尔可夫模型并不是俄罗 ...
- 机器学习算法总结(六)——EM算法与高斯混合模型
极大似然估计是利用已知的样本结果,去反推最有可能(最大概率)导致这样结果的参数值,也就是在给定的观测变量下去估计参数值.然而现实中可能存在这样的问题,除了观测变量之外,还存在着未知的隐变量,因为变量未 ...
随机推荐
- android 图片网络下载github开源框架之Universal-Image-Loader
最近在做妙趣剪纸项目,剪纸应用项目链接.发扬传统文化,大家多多关注. 需要自己搭建服务器,我用的是新浪sae,简直秒杀京东云几条街,把图片放在网上下载,但是图片经常下载要遇到很多问题,包括oom等.所 ...
- 求链表倒数第n个元素
提示:设置一前一后两个指针,一个指针步长为1,另一个指针步长为n,当一个指针走到链表尾端时, 另一指针指向的元素即为链表倒数第n个元素. #include <stdio.h> #inclu ...
- Linux命令—压缩及其他
(1)为了更好的传送和保存文件,需要对某些文件和目录进行压缩和解压缩操作,Linux 提供了强大的压缩.解压缩命令,常用的tar命令. (2)在Linux中,如果要使用储存设备(硬盘.光驱.移动 ...
- 百度地图SDK3.4的使用
使用过百度地图的开发者应该都知道原始百度地图的开发的基本流程,但是随着百度地图的更新,百度地图的api有了翻天覆地的变化,最新版本的sdk为v3.4 2015年4月14日上线,优化了许多接口的设计,简 ...
- Spark集群术语
Spark集群术语解析 1. Application Application是用户在Spark上构建(编写)的程序,包含driver program 和executors(分布在集群中多个节点上运行的 ...
- 如何使用excel画甘特图
甘特图小伙伴们都非常的熟悉,首先小编简单的向各位小伙伴介绍一下什么是甘特图,甘特图内在思想简单,即以图示的方式通过活动列表和时间刻度形象地表示出任何特定项目的活动顺序与持续时间.基本是一条线条图,横轴 ...
- 让 Google Test 出错时断点
Google Test 缺省是出错退出. 如果最后的出错行在系统库中,那就没什么帮助. 如果是调试运行,直接退出根本就不知道哪里出错了. 后来添加了一个运行参数: --gtest_break_on_f ...
- 带吸附效果的ViewPager(一)
什么叫吸附效果?先看一个示例更为直观,借用网上的一个效果图: 类似这种效果的app很多,网上的实现方法也是很多,但各种重写各种监听又令人不胜其烦,今日突发奇想,顺着自己的思路实现了类似的效果,不敢独享 ...
- 04 AutoCompleteTextView
作用:输入部分文字跳处下拉框列出相应的条目 <pre name="code" class="html"> <!-- 当文本框出现两个字符才开始 ...
- 深入剖析Tomcat会话机制
1缓存机制 Tomcat默认将Session保存到内存中.但同时,Tomcat也提供了PersistentManager配合不同的Store实现的方式,使Session可以被保存到不同地方(Datab ...