【机器学习】--LDA初始和应用

一、前述

LDA是一种 非监督机器学习 技术，可以用来识别大规模文档集（document collection）或语料库（corpus）中潜藏的主题信息。它采用了词袋（bag of words）的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序，这简化了问题的复杂性，同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。由于 Dirichlet分布随机向量各分量间的弱相关性（之所以还有点“相关”，是因为各分量之和必须为1），使得我们假想的潜在主题之间也几乎是不相关的，这与很多实际问题并不相符，从而造成了LDA的又一个遗留问题。

二、具体过程

对于语料库中的每篇文档，LDA定义了如下生成过程（generativeprocess）：

1.对每一篇文档，从主题分布中抽取一个主题；

2.从上述被抽到的主题所对应的单词分布中抽取一个单词；

3.重复上述过程直至遍历文档中的每一个单词。

语料库中的每一篇文档与T（通过反复试验等方法事先给定）个主题的一个多项分布 （multinomialdistribution）相对应，将该多项分布记为θ。每个主题又与词汇表（vocabulary）中的V个单词的一个多项分布相对应，将这个多项分布记为φ。

三、案例

假设文章1开始有以下单词：

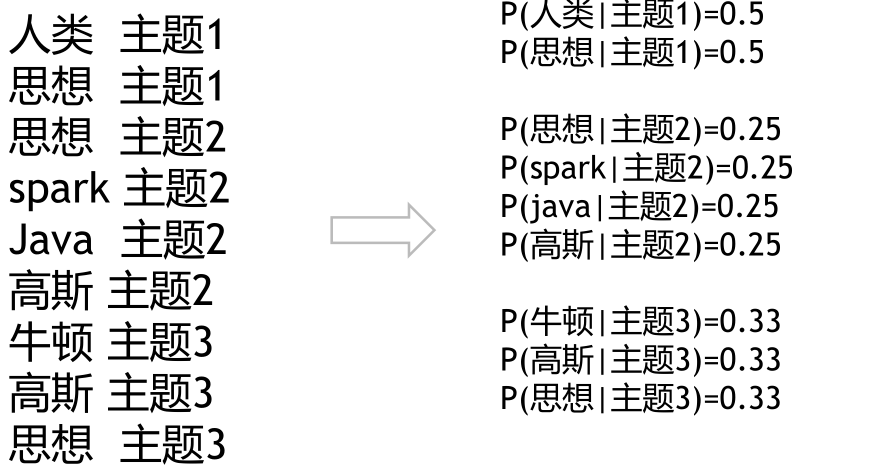
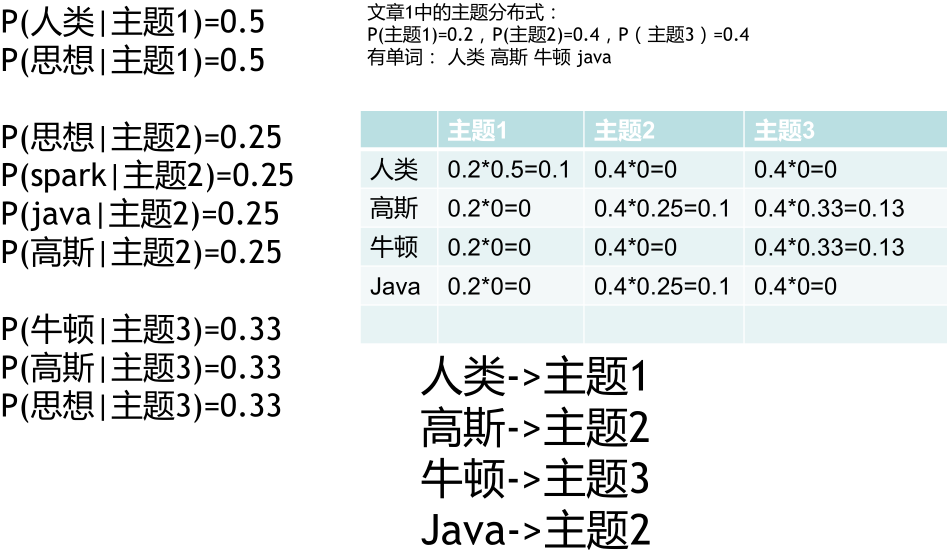
高斯分为主题二，是因为有一定的概率。

如此反复，当各个概率分布不再发生变化时，即完成了收敛和训练过程
训练思想仍然是EM算法（摁住一个，去计算另一个）
对比K-means

实际工程过程中：
每一个主题对每一个词都有一个基本出现次数（人工设定）
每一篇文章在各个主题上都有一个基本出现词数

步骤：

新来一片文章，需要确定它的主题分布：
先随机化主题分布
1.根据主题分布和主题-单词模型，找寻每个
单词所对应的主题
2.根据单词主题重新确定主题分布
1,2反复，直到主题分布稳定 最终得到两个模型：
1.每篇文章的主题分布
2.每个主题产生词的概率

用途：
1.根据文章的主题分布，计算文章之间的相似性
2.计算各个词语之间的相似度

四、代码

# -*- coding: utf-8 -*-

import jieba
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation

for i in range(4):
    with open('./data/nlp_test%d.txt' % i, encoding='UTF-8') as f:
        document = f.read()

        document_cut = jieba.cut(document)
        result = ' '.join(document_cut)
        print(result)
        with open('./data/nlp_test%d.txt' % (i+10), 'w', encoding='UTF-8') as f2:
            f2.write(result)
    f.close()
    f2.close()

# 从文件导入停用词表
stpwrdpath = "./data/stop_words.txt"
stpwrd_dic = open(stpwrdpath, 'r', encoding='UTF-8')
stpwrd_content = stpwrd_dic.read()
# 将停用词表转换为list
stpwrdlst = stpwrd_content.splitlines()
stpwrd_dic.close()
print(stpwrdlst)

# 向量化 不需要tf_idf
corpus = []
for i in range(4):
    with open('./data/nlp_test%d.txt' % (i+10), 'r', encoding='UTF-8') as f:
        res = f.read()
        corpus.append(res)
    print(res)

cntVector = CountVectorizer(stop_words=stpwrdlst)
cntTf = cntVector.fit_transform(corpus)
print(cntTf)

# 打印输出对应关系
# 获取词袋模型中的所有词
wordlist = cntVector.get_feature_names()
# 元素a[i][j]表示j词在i类文本中的权重
weightlist = cntTf.toarray()
# 打印每类文本的词语权重，第一个for遍历所有文本，第二个for便利某一类文本下的词语权重
for i in range(len(weightlist)):
    print("-------第", i, "段文本的词语权重------")
    for j in range(len(wordlist)):
        print(wordlist[j], weightlist[i][j])

lda = LatentDirichletAllocation(n_components=3,#3个话题
                                learning_method='batch',
                                random_state=0)
docres = lda.fit_transform(cntTf)

print("文章的主题分布如下：")
print(docres)
print("主题的词分布如下：")
print(lda.components_)